Содержание
- 2. Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений
- 3. Джордж Буль
- 4. Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или
- 5. Пример: «Трава зеленая» -истинное высказывание. «Лев – птица» - ложное высказывание.
- 6. Не всякое предложение является логическим высказыванием. Пример: «ученик десятого класса» «информатика — интересный предмет».
- 7. Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если... , то", "тогда и только
- 8. Высказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются
- 9. Пример: Элементарные высказывания: «Петров — врач», «Петров — шахматист» Составные высказывания: "Петров — врач и шахматист",
- 10. Чтобы обращаться к логическим высказываниям, их обозначают буквами. Пример: А = «Луна – спутник Земли», А
- 11. Пример: А ="Тимур поедет летом на море", В = "Тимур летом отправится в горы". А и
- 12. Операции над логическими высказываниями
- 13. Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности
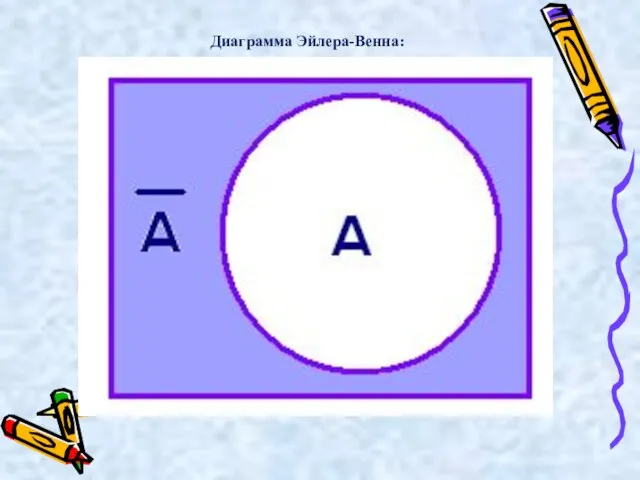
- 14. Логическое «отрицание» (инверсия или НЕ) обозначается чертой над высказыванием Ā .
- 15. Диаграмма Эйлера-Венна:
- 16. Пример: А = «Луна — спутник Земли» А = "Луна — не спутник Земли"
- 17. Высказывание А истинно, когда A ложно, и ложно, когда A истинно. Таблица истинности
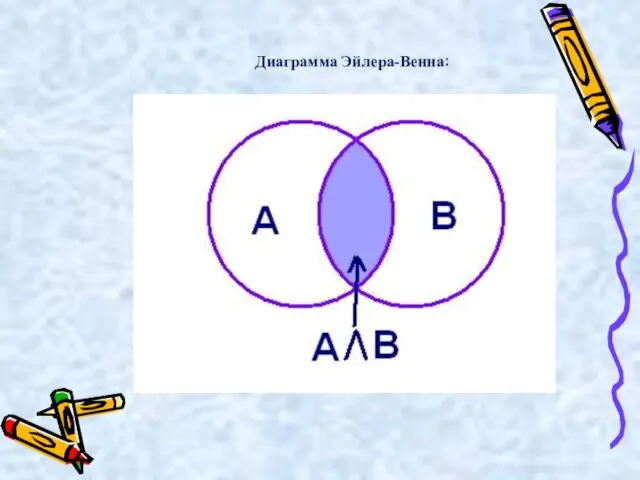
- 18. Логическое умножение ( «и», конъюнкция (лат. conjunctio — соединение)) обозначается точкой " . " (может также
- 19. Диаграмма Эйлера-Венна:
- 20. Пример: А = «10 делится на 2», А= 1 В = «5 больше 3», В =
- 21. Высказывание А · В истинно тогда и только тогда, когда оба высказывания А и В истинны.
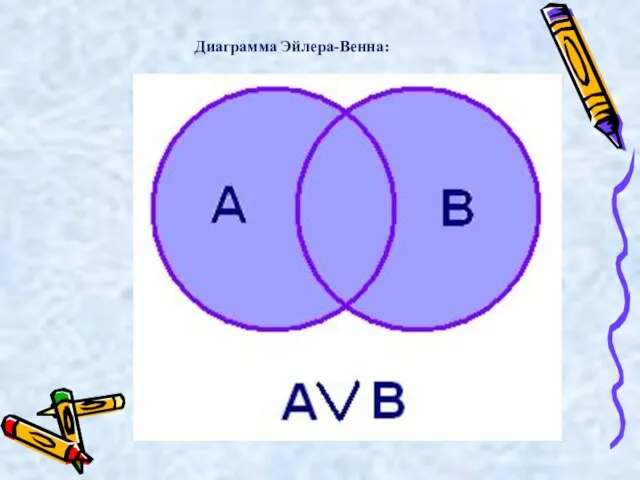
- 22. Логическое сложение ( «или», дизъюнкция (лат. disjunctio — разделение) обозначается знаком v или +. А V
- 23. Диаграмма Эйлера-Венна:
- 24. Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны.
- 25. Импликация (лат. implico — тесно связаны) -операция, выражаемая связками «если ..., то…», «из ... следует…», «...
- 26. Высказывание А В ложно тогда и только тогда, когда А истинно, а В – ложно. Таблица
- 27. Эквиваленция (двойная импликация) - операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «... равносильно
- 28. Высказывание А В истинно тогда и только тогда, когда значения А и В совпадают. Таблица истинности
- 29. А = «10 делится на 2», А= 1 В = «5 больше 3», В = 1
- 30. Порядок выполнения логических операций 1.Сначала выполняется операция отрицания (“не”), 2. Затем конъюнкция (“и”), 3. После конъюнкции
- 31. A → B = ¬ A ∨ B Законы де Моргана ¬ (A ∧ B) =
- 33. Скачать презентацию



























 Семейный бюджет (3 класс)
Семейный бюджет (3 класс) Природа и люди Древней Индии
Природа и люди Древней Индии Необычный уличный арт: Канализационные люки из Японии
Необычный уличный арт: Канализационные люки из Японии Rastlinné telo ako celok
Rastlinné telo ako celok Основные подсистемы системы управления организации
Основные подсистемы системы управления организации Оформление выходных сведений электронных изданий
Оформление выходных сведений электронных изданий Управление человеческими ресурсами
Управление человеческими ресурсами Роль школьной телестудии в образовательном и воспитательном процессе.
Роль школьной телестудии в образовательном и воспитательном процессе. ЭНДОВАСКУЛЯРНЫЕ И ГИБРИДНЫЕ МЕТОДЫ ЛЕЧЕНИЯ ПАТОЛОГИЙ ДУГИ АОРТЫ
ЭНДОВАСКУЛЯРНЫЕ И ГИБРИДНЫЕ МЕТОДЫ ЛЕЧЕНИЯ ПАТОЛОГИЙ ДУГИ АОРТЫ Презентация на тему Суд и процесс в Древнем Риме
Презентация на тему Суд и процесс в Древнем Риме  Илья Ильич Мечников 165 лет со дня рождения
Илья Ильич Мечников 165 лет со дня рождения Prezentatsiya Voytsehovskaya
Prezentatsiya Voytsehovskaya Бартоломео Франческо Растрелли
Бартоломео Франческо Растрелли Словарная работа
Словарная работа Китайский чай с молоком
Китайский чай с молоком Создание специальных образовательных условий в образовательной организации
Создание специальных образовательных условий в образовательной организации «Творчество К.И.Чуковского»
«Творчество К.И.Чуковского» Презентация на тему Сфера и шар
Презентация на тему Сфера и шар Работа секретаря с документами, содержащими конфиденциальную информацию
Работа секретаря с документами, содержащими конфиденциальную информацию Startup Tour/2022
Startup Tour/2022 Юридическая ответственность
Юридическая ответственность Зона смешанных лесов
Зона смешанных лесов Диагностики профильной направленности личности. Основы выбора профессии
Диагностики профильной направленности личности. Основы выбора профессии А.С. Пушкин
А.С. Пушкин Презентация на тему Антибиотики
Презентация на тему Антибиотики  Презентация на тему Возникновение ислама
Презентация на тему Возникновение ислама  The Gerund
The Gerund Мобилизационная готовность спортсмена высшей квалификации. Предпосылки и общие положения
Мобилизационная готовность спортсмена высшей квалификации. Предпосылки и общие положения