Презентация на тему Степень и ее свойства

Пусть кто-нибудь
попробует вычеркнуть
из математики степени,
и он увидит, что
без них далеко
не уедешь.
М.В. Ломоносов

ЗНАНИЕ ТЕОРИИ ОБЯЗАТЕЛЬНО!!!
Определение степени
=
раз
n
а
п
а
а
а
•
•
•

1. Запишите произведение в виде степени:
Примеры применения
9·9·9 =
9³
(-х)(-х)(-х)(-х)(-х) =
(а-с)(а-с) =
2. Найдите значение степени:
(-2)⁴ =
=
(- 0,1)³ =
(- х)⁵
(а – с)²
16
- 0,001
—
1
32
—

10² - 3² =
(10 -3)² =
(6 - 8)⁵ =
10 - 5·2⁴ =
- 1³ + ( -2)³ =
- 6² - ( -1)⁴ =
7² =
( -2)⁵ =
10 - 5·16 = 10 - 80 =
- 1 - 8 =
- 36 - 1 =
100 – 9 =
91
49
- 32
- 70
- 9
- 37

ЗНАНИЕ ТЕОРИИ ОБЯЗАТЕЛЬНО!!!
Показатели умножаем
Показатели складываем
a
a
a
т
т - п
:
=
( а ≠ 0, т > п)
Показатели вычитаем
а
1
,(а ≠ 0)
n
а b
n
n
( а ) = а
т п
т
п
1
a
a
a
=
т + п
т
п
2
п
3
=
0
4
( аb)
=
5
0⁰ не имеет смысла
6
а
b
—
b
—
а
n
n
n
(
(
=
b
≠ 0
(
)

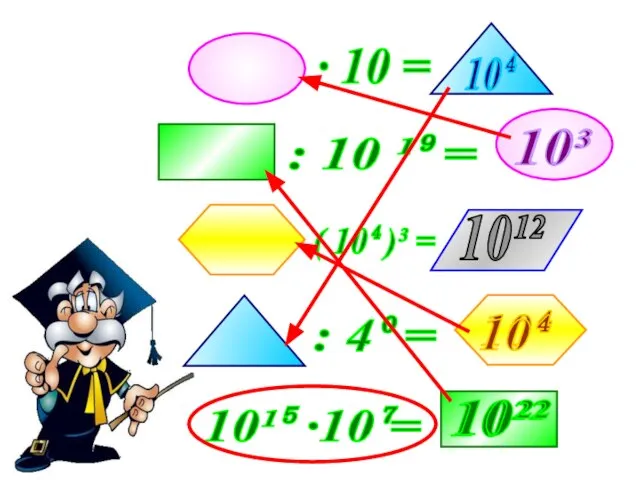
10²²
10²²
10³
10³
10⁴
10⁴
10⁴
10⁴
10¹²

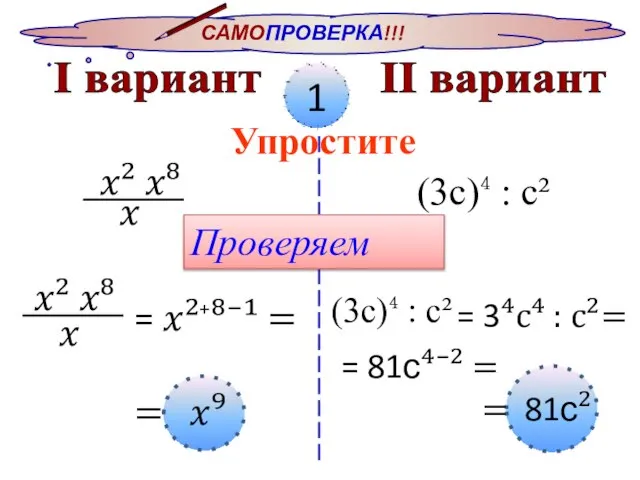
САМОПРОВЕРКА!!!
I вариант II вариант
1
Упростите
?² ?⁸
?
(3с)⁴ : с²
Проверяем
?² ?⁸
?
= ?²⁺⁸⁻¹ =
= ?⁹
(3с)⁴ : с²
= 3⁴с⁴ : с²=
= 81с⁴⁻² =
= 81с²

САМОПРОВЕРКА!!!
I вариант II вариант
2
Вычислите
Проверяем
25¹³ : 5²³
27¹⁰ : 9¹⁵
25¹³ : 5²³ =
= (5²)¹³ : 5²³ =
= 5²⁶ : 5²³ = 5³ =
= 125
27¹⁰ : 9¹⁵ =
= (3³)¹⁰ : (3²)¹⁵ =
= 3³⁰ : 3³⁰ =
= 1

САМОПРОВЕРКА!!!
I вариант II вариант
3
Найдите значение выражения
2⁵ · (2³)⁴
2¹³
Проверяем
(5⁸)² · 5⁷
5²²
2⁵ · (2³)⁴
2¹³
2⁵ · 2¹²
2¹³
= 2⁵ ⁺¹² ⁻ ¹³ = 2⁴ =
= 16
=
=
(5⁸)² · 5⁷
5²²
5²²
=
=
5¹⁶ · 5⁷
= 5¹⁶ ⁺ ⁷ ⁻²² =
= 5

САМОПРОВЕРКА!!!
I вариант II вариант
4
Упростите
2 · 5ⁿ
5ⁿ⁺¹ + 5ⁿ⁻¹
Проверяем
10 · 3ⁿ
3ⁿ⁺¹ - 3ⁿ⁻¹
2 · 5ⁿ
5ⁿ⁻¹(5²+1)
2 · 5ⁿ
5ⁿ⁻¹ · 26
=
=
10 · 3ⁿ
3ⁿ⁻¹(3² - 1)
3ⁿ⁻¹ · 8
=
=
10 · 3ⁿ
=
=
1
13
·5ⁿ⁻ⁿ⁺¹ =
1
13
· 5 =
13
5
=
5
5
4
4
4
4
· 3ⁿ⁻ⁿ⁺¹ =
· 3 =
=
=
15
3
3

САМОПРОВЕРКА!!!
I вариант II вариант
5
Вычислите
( - 2⁰ )³
( ( 1² )² )²
6
Сравните с нулем
(-5)² · (-3,2)³… 0
-3,92² · (- 4)⁹… 0

Верно ли выполнены действия?
5·5·5·5 = 4⁵
( - 2х )³ = - 2х³
(- 3)² = - 9
2³ · 2⁷ = 2²¹
3¹⁰ : 3⁵ = 3²
2³ + 2² = 2⁵
5³ · 5⁴ = 25⁷
5⁷
12
2¹⁰
9
- 8х³
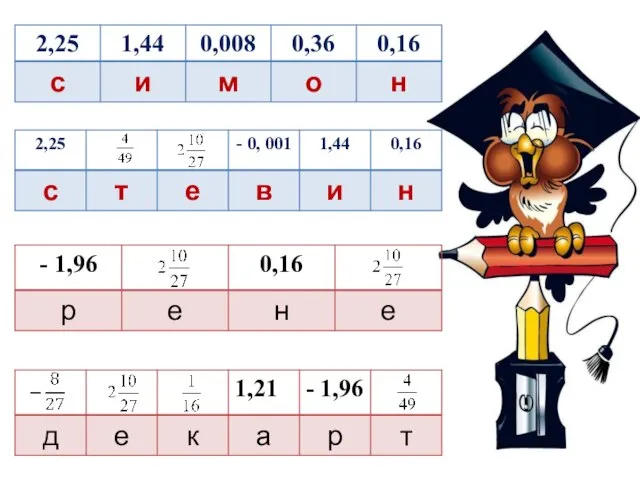
5⁴

История создания современной теории степеней
Выполните вычисления. Заполните таблицы буквами, учитывая найденные ответы.
0,4²
0,2³
(- 0,6)²
(- 0,1)³
1,1²
(- 1,2)²
(- 1,5)²
- 1,4²
с
р
т
к
д
е
и
а
в
о
м
н

Си́мон Сте́вин (нидерл. Simon Stevin, 1548—1620) — фламандский математик-универсал, инженер.
Нидерландский математик Симон Стевин в 16-17 веках предпринял первые шаги к построению современной теории степени. Он обозначал неизвестную величину кружком, а внутри его указывал показатели степени.
Запись 3(3)+5(2)–4 обозначала такую современную запись
33 + 52 – 4

Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2. Позднее Ньютон распространил эту форму записи на отрицательные и дробные показатели (1676), трактовку которых к этому времени уже предложил Стевин.
Мыслю, следовательно существую.
Рене Декарт
Французский философ и математик.

Величие человека –
в его способности мыслить.
Б.Паскаль
а¹² а * : а¹⁰ = а⁵
а а* = а⁷
( а² )³  = а²⁴
( a² b )* = a¹⁰ b⁵
(  a* b⁴ )³ = 8 a⁹ b¹²
3
6
a¹⁸
5
2
3

1
Дорогу осилит идущий,
а математику мыслящий.
Т. Эдисон
Вычислите:
5²¹+ 5²¹ + 5²¹ + 5²¹ + 5²¹
5²⁰

Запишите число 9 четырьмя тройками
с использованием знаков действий
(включая возведение в степень).
2
9 = 3² = 3³ ¯ ¹ = 3 ³¯
3
3
3
Запишите число 1024 четырьмя четвёрками с использованием знаков действий (включая возведение в степень).
1024 = 2¹⁰ = 4⁵ = 4⁴⁺¹ = 4⁴⁺
4
⁴

Домашнее задание
п.п. 18 – 20, № 535(б,г,е), 547.
Заполните свободные клетки квадрата так, чтобы произведение выражений каждого столбца, каждой строки и диагонали равнялось
Такой квадрат называется магическим.

Высшее назначение математики – находить порядок в хаосе, который нас окружает.
Норберт Винер

Тест № 11
Свойства степени
с натуральным показателем
Вариант 1 Вариант 2
стр. 38 стр. 40

Математика выявляет порядок,
симметрию и определённость,
а это – важнейшие виды прекрасного. Аристотель
Мир фракталов