Содержание
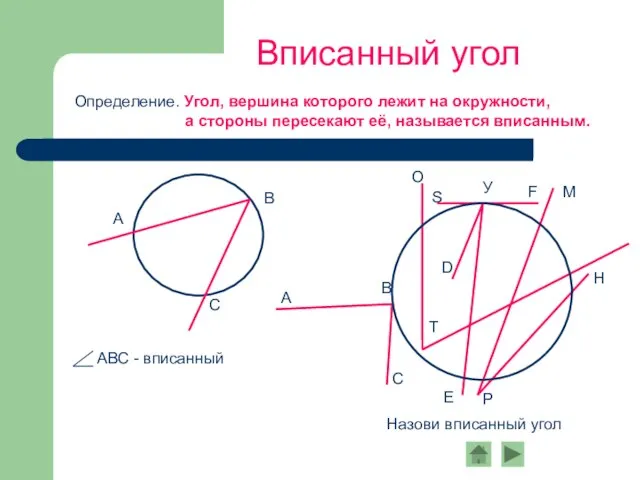
- 2. Определение. Угол, вершина которого лежит на окружности, а стороны пересекают её, называется вписанным. Вписанный угол
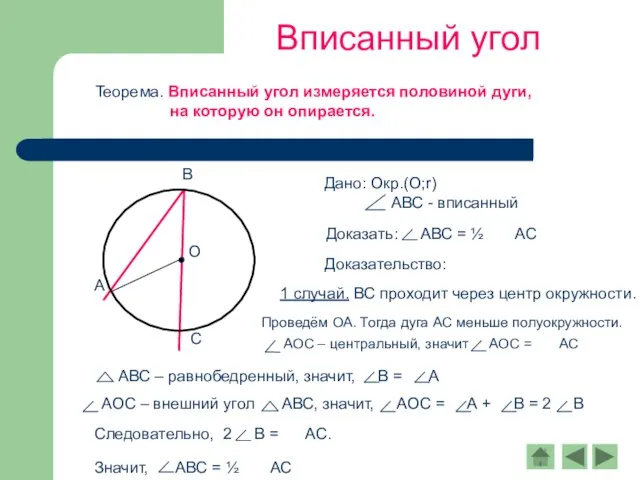
- 3. Вписанный угол Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство: 1 случай. ВС
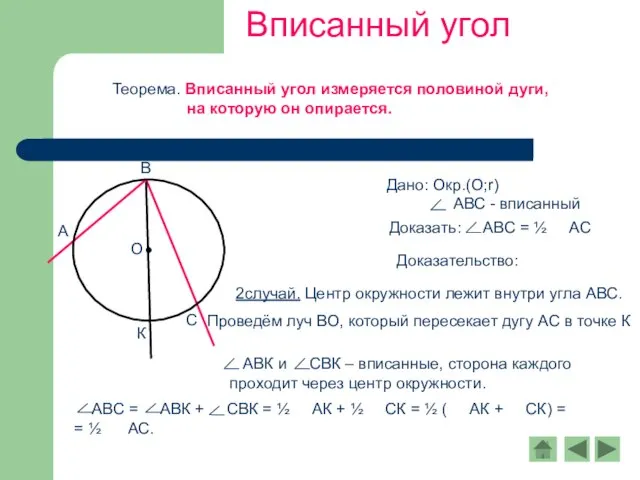
- 4. Вписанный угол Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство: 2случай. Центр окружности
- 5. Вписанный угол Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство: 3 случай. Центр
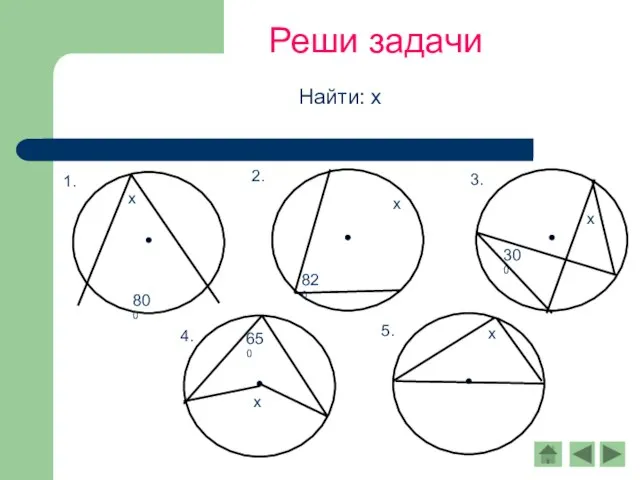
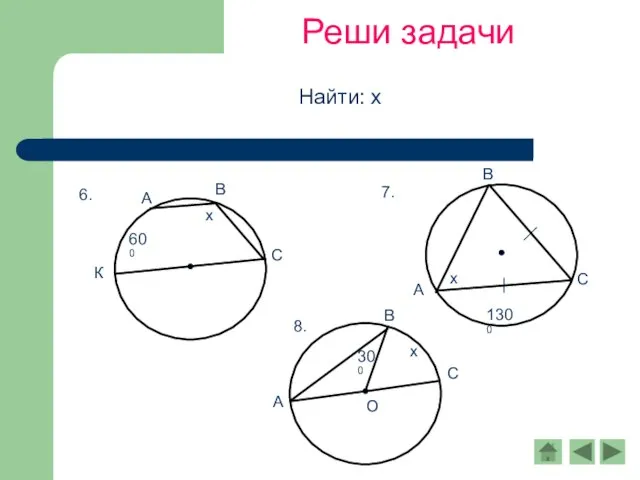
- 6. Реши задачи Найти: х
- 7. Реши задачи Найти: х
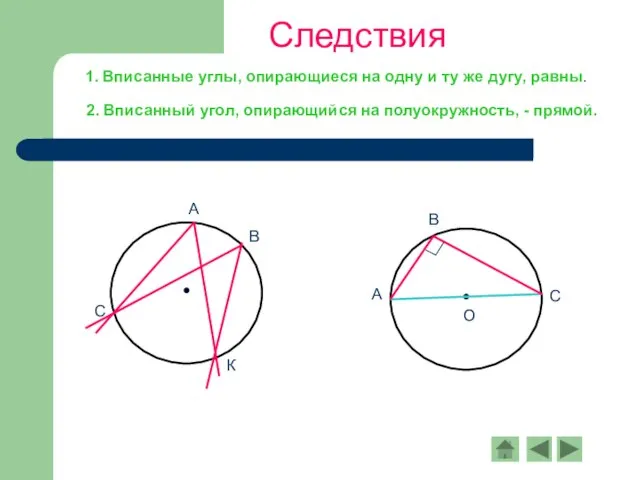
- 8. Следствия 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны. 2. Вписанный угол, опирающийся
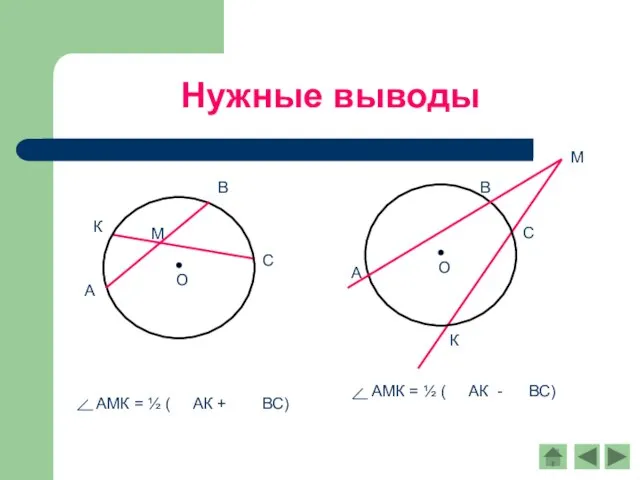
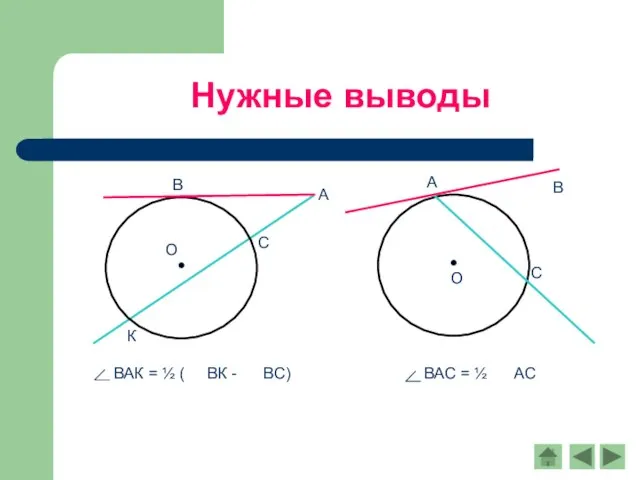
- 9. Нужные выводы
- 10. О С Нужные выводы
- 11. Свойство пересекающихся хорд Теорема. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению
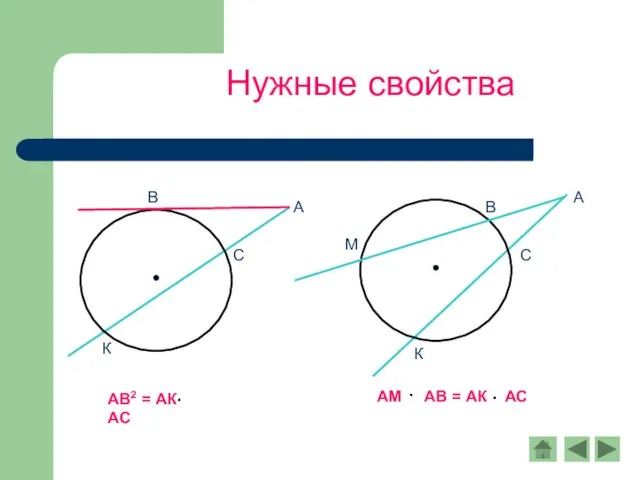
- 12. Нужные свойства
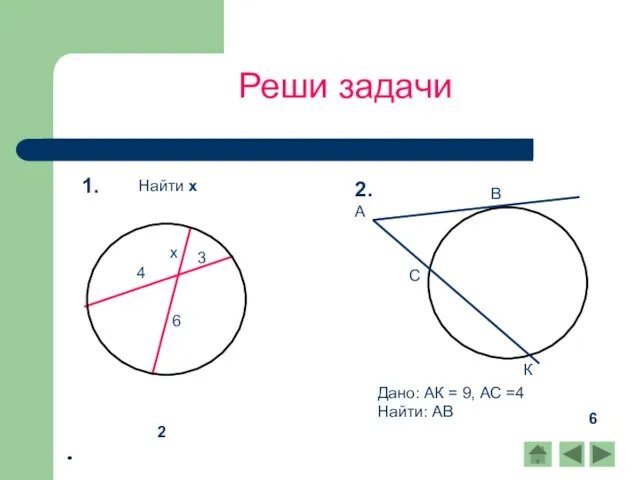
- 13. Реши задачи 2 С 6
- 15. Скачать презентацию


 ТВОРЧЕСКИЙ ПРОЕКТ
ТВОРЧЕСКИЙ ПРОЕКТ Концепция стратегического управления Arthur d.little. Модель ADL/LC Дисциплина: Международный маркетинг
Концепция стратегического управления Arthur d.little. Модель ADL/LC Дисциплина: Международный маркетинг В путешествие за меткими словами
В путешествие за меткими словами Сходство М.Ю. Лермонтова и его героя Мцыри
Сходство М.Ю. Лермонтова и его героя Мцыри Перспективы развития электроэнергетики Дальнего Востока
Перспективы развития электроэнергетики Дальнего Востока Смеси
Смеси Диагностическая работа по русскому языку 2 класс
Диагностическая работа по русскому языку 2 класс Гидроэнергетические ресурсы Центральной Азии
Гидроэнергетические ресурсы Центральной Азии Культура в эпоху Возрождения
Культура в эпоху Возрождения Управление маркетингом
Управление маркетингом Спорт в США
Спорт в США МУЗЕЙ ШКОЛЫ №25
МУЗЕЙ ШКОЛЫ №25 Диагностика школьной дезадаптации
Диагностика школьной дезадаптации Презентация на тему Лувр. Париж
Презентация на тему Лувр. Париж  Чешская республика
Чешская республика Строение и развитие мужских половых клеток
Строение и развитие мужских половых клеток Региональные и федеральные службы помощи
Региональные и федеральные службы помощи Немного о себе
Немного о себе Межкультурные различия в деловой этике
Межкультурные различия в деловой этике Образ Дома в романе М.Булгакова «Белая гвардия»
Образ Дома в романе М.Булгакова «Белая гвардия» Тракторист-машинист сельскохозяйственного производства
Тракторист-машинист сельскохозяйственного производства .
. Дёшево и мило. Коврик из помпонов
Дёшево и мило. Коврик из помпонов Программа воспитания как инструмент развития школы в современных условиях
Программа воспитания как инструмент развития школы в современных условиях ГИА-9 2012
ГИА-9 2012 Моя профессия Монтажник санитарно-технических, вентиляционных систем и оборудования
Моя профессия Монтажник санитарно-технических, вентиляционных систем и оборудования МКОУ Элисенваарская СОШ. Юбилейные выпуски
МКОУ Элисенваарская СОШ. Юбилейные выпуски 543814
543814