ПРЕЗЕНТАЦИЯ ПО ТЕМЕНЕРАВЕНСТВА /8 класс/

СОДЕРЖАНИЕ ТЕМЫ
Введение
Виды неравенств
Свойства числовых
неравенств
Действия с двойными
неравенствами
Доказательства
неравенств
Решение линейных неравенств
Система линейных
неравенств
Решение системы
линейных неравенств
Дидактический
материал по теме
Контрольные вопросы
по теме

При сравнении двух действительных
чисел Х и У возможны три случая:
Х=У (если Х – У = 0)
Х>У (если Х – У > 0)
Х<У (если Х – У < 0)
Запись Х≥У (Х≤У) означает, что либо
Х>У, либо Х=У и читается так:
«Х больше или равно У» или
«Х не меньше У»
Запись, в которой два числа или два выражения, содержащие
переменные, соединены знаком >,<,≥ или≤ называется
неравенством.

Неравенства могут быть :
Строгими (неравенство
составлено с помощью
знаков > или < )
Нестрогими (неравенство
составлено с помощью
знаков ≤ или ≥ )
Двойными (вместо двух
неравенств х<а, а<у
употребляется запись
х

Числовыми (неравенство содержит только числа)
Верными (если неравенство представляет
собой истинное высказывание: 2<3)
Неверными ( если неравенство представляет собой ложное высказывание: -4>15)
Равносильными (если
множества решений этих
неравенств совпадают)

Рассмотрим свойства числовых неравенств :
1. для любых чисел a и b: если a>b, то b
2. для любых чисел a,b и c таких, что a>b, a b>c, верно: a>c (свойство транзитивности)
3. если a>b и c-любое число, то a+c=b+c
4. если a>b и c>0, то ac>bc
5. если a>b и c<0, то ac
6. если a>b>0, то

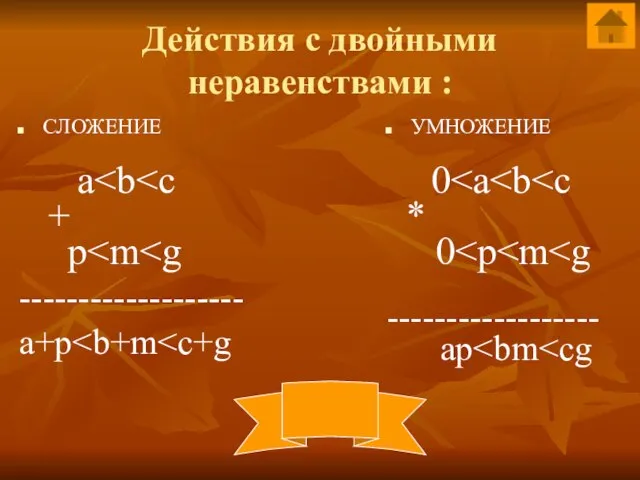
Действия с двойными неравенствами :
СЛОЖЕНИЕ
a
+
p
-------------------
a+p
УМНОЖЕНИЕ
0
*
0
------------------ ap

При доказательстве неравенств используются определения понятий больше или меньше.
Пример:
Доказать, что
Решение:
Рассмотрим разность
Следовательно,

Линейным неравенством называется неравенство вида ax+b>0 (или ax+b<0).
Если a>0, то неравенство ax+b>0
равносильно неравенству
Если а<0, то неравенство ax+b>0
равносильно неравенству

Если ставится задача найти множество общих решений двух или нескольких неравенств, то говорят, что нужно решить систему неравенств.
Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств.

Неравенства, входящие в систему, объединяются фигурной скобкой. Иногда системы неравенств записывают в виде двойного неравенства.
Например, систему
3х-1>2,
3x-1<8
можно записать так: 2<3x-1<8

Решение системы линейных неравенств с
одной переменной сводится к следующим
случаям. Будем считать, что a

Дидактический
материал
1. Найдите наибольшее целое число x, удовлетворяющее
неравенству:
2. Пусть а

3. Докажите, что:
а) если , то ;
б) если , то ;
в) если , где а- неотрицательное число.
4. Пусть -3
а) (а+b);
b) 3a+2b.
5. Решить неравенство:

7. Решите двойное неравенство:
8. Решить систему линейных неравенств:

Контрольные вопросы по теме
1. Дайте определение неравенства.
2. Какие виды неравенств вы знаете ?
3. Истинно ли высказывание:
4. Сформулируйте свойства
неравенств.
5. Докажите, что если a>b и b>c, то
a>c.
6. Докажите, что если a
0, то
ax>bx.

7. Сформулируйте правила действий с неравенствами.
8. Что значит решить неравенство, содержащее
переменную ?
9. Какие неравенства называются равносильными?
10.Что значит решить систему неравенств ?