Презентация доклад

Понятие дисперсионного анализа.
Дисперсионный анализ – анализ изменчивости признака под влиянием каких-либо контролируемых переменных факторов.
В основе дисперсионного анализа лежит предположение о том, что одни переменные могут рассматриваться как причины (факторы, независимые переменные), а другие как следствия (зависимые переменные).
Независимые переменные называют иногда регулируемыми факторами именно потому, что в эксперименте исследователь имеет возможность варьировать ими и анализировать получающийся результат.

Цель и задачи дисперсионного анализа
Основной целью дисперсионного анализа является исследование значимости различия между средними с помощью сравнения (анализа) дисперсий.
Обобщенно задача дисперсионного анализа состоит в том, чтобы из общей
вариативности признака выделить три частные вариативности:
вариативность, обусловленную действием каждой из исследуемых независимых переменных;
вариативность, обусловленную взаимодействием исследуемых независимых переменных;
вариативность случайную, обусловленную всеми неучтенными обстоятельствами.

Гипотезы при дисперсионном анализе
При дисперсионном анализе определяют удельный вес суммарного воздействия одного или нескольких факторов. Существенность влияния фактора определяется путём проверки гипотез:
H0: μ1 = μ2 = ... = μa, где a - число классов градации - все классы градации имеют одно значение.
H1: не все μi равны - не все классы градации имеют одно значение средних.

Проверка значимости, разброс данных.
Проверка значимости в дисперсионном анализе основана на сравнении дисперсии, обусловленной межгрупповым разбросом (называемой средним квадратом эффекта или MSэффект) и дисперсии, обусловленной внутригрупповым разбросом (называемой средним квадратом ошибки или MSошибка). Если верна нулевая гипотеза (равенство средних в двух популяциях), то можно ожидать сравнительно небольшое различие в выборочных средних из-за случайной изменчивости. Поэтому при нулевой гипотезе внутригрупповая дисперсия будет практически совпадать с общей дисперсией, подсчитанной без учета группой принадлежности. Полученные внутригрупповые дисперсии можно сравнить с помощью F-критерия, проверяющего, действительно ли отношение дисперсий значимо больше 1.

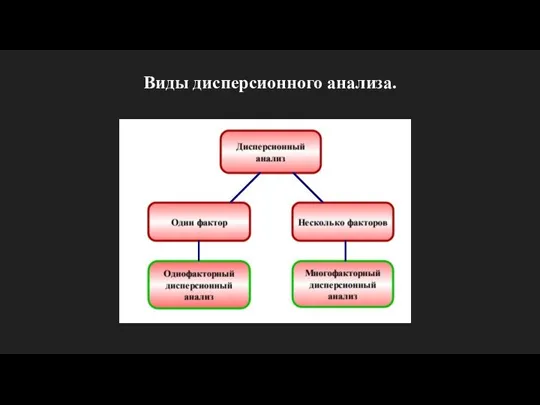
Виды дисперсионного анализа.

Однофакторный дисперсионный анализ
Однофакторный дисперсионный анализ основан на том, что сумму квадратов отклонений статистического комплекса возможно разделить на компоненты:
SS = SSa + SSe, где
SS - общая сумма квадратов отклонений,
SSa - объяснённая влиянием фактора a сумма квадратов отклонений,
SSe - необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки.

Однофакторный дисперсионный анализ
Чтобы провести однофакторный дисперсионный анализ данных статистического комплекса, нужно найти фактическое отношение Фишера - отношение дисперсии, объяснённой влиянием фактора (межрупповой), и необъяснённой дисперсии (внутригрупповой):
и сравнить его с критическим значением Фишера
Дисперсии рассчитываются следующим образом:

Двухфакторный дисперсионный анализ
Двухфакторный дисперсионный анализ применяется для того, чтобы проверить возможную зависимость результативного признака от двух факторов - A и B. Тогда a - число градаций фактора A и b - число градаций фактора B. В статистическом комплексе сумма квадратов остатков разделяется на три компоненты:

Двухфакторный дисперсионный анализ
SS = SSa + SSb + SSe,

Двухфакторный дисперсионный анализ
Дисперсии вычисляются следующим образом:

Двухфакторный дисперсионный анализ
Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются две нулевые гипотезы и соответствующие альтернативные гипотезы:

Примеры дисперсионного анализа результатов
имитационных экспериментов в среде GPSS World

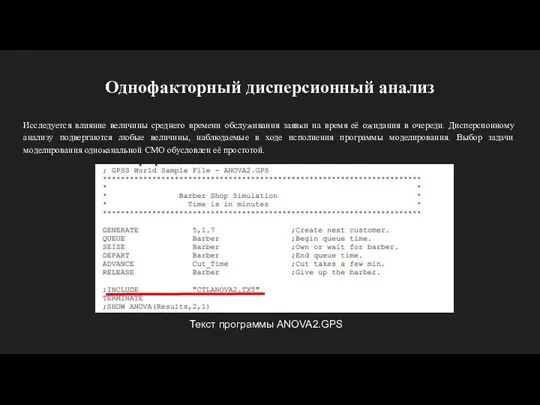
Однофакторный дисперсионный анализ
Исследуется влияние величины среднего времени обслуживания заявки на время её ожидания в очереди. Дисперсионному анализу подвергаются любые величины, наблюдаемые в ходе исполнения программы моделирования. Выбор задачи моделирования одноканальной СМО обусловлен её простотой.
Текст программы ANOVA2.GPS

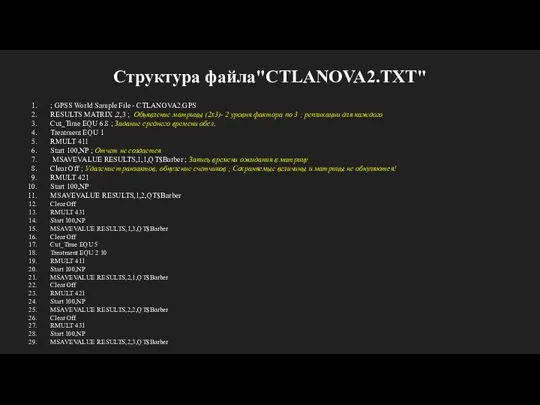
Структура файла"CTLANOVA2.TXT"
; GPSS World Sample File - CTLANOVA2.GPS
RESULTS MATRIX ,2,3 ; Объявление матрицы (2х3)- 2 уровня фактора по 3 ; репликации для каждого
Cut_Time EQU 6.8 ; Задание среднего времени обсл.
Treatment EQU 1
RMULT 411
Start 100,NP ; Отчет не создается
MSAVEVALUE RESULTS,1,1,QT$Barber ; Запись времени ожидания в матрицу
Clear Off ; Удаление транзактов, обнуление счетчиков ; Сохраняемые величины и матрицы не обнуляются!
RMULT 421
Start 100,NP
MSAVEVALUE RESULTS,1,2,QT$Barber
Clear Off
RMULT 431
Start 100,NP
MSAVEVALUE RESULTS,1,3,QT$Barber
Clear Off
Cut_Time EQU 5
Treatment EQU 2 10
RMULT 411
Start 100,NP
MSAVEVALUE RESULTS,2,1,QT$Barber
Clear Off
RMULT 421
Start 100,NP
MSAVEVALUE RESULTS,2,2,QT$Barber
Clear Off
RMULT 431
Start 100,NP
MSAVEVALUE RESULTS,2,3,QT$Barber

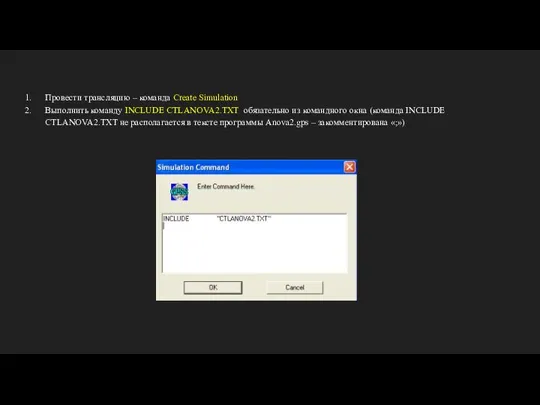
Провести трансляцию – команда Create Simulation
Выполнить команду INCLUDE CTLANOVA2.TXT обязательно из командного окна (команда INCLUDE CTLANOVA2.TXT не располагается в тексте программы Anova2.gps – закомментирована «;»)

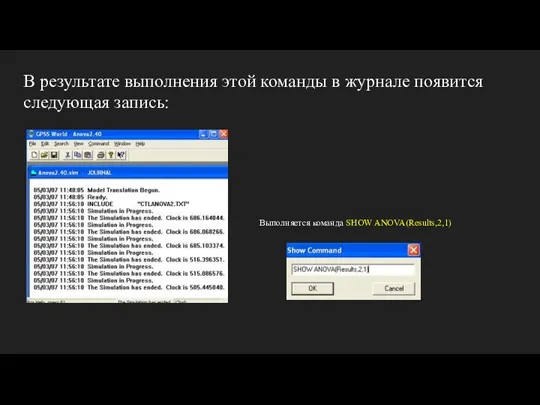
В результате выполнения этой команды в журнале появится следующая запись:
Выполняется команда SHOW ANOVA(Results,2,1)

Результат выполнения этой команды появляется в виде записи в журнале
В качестве пояснения синтаксиса команды ANOVA ниже приводится выдержка из Help GPSS World:
ANOVA Syntax
StandardError =ANOVA(ResultMatrixName,ReplicateDimension,InteractionLimit)
Arguments
ResultMatrixName - The GPSS Matrix containing the results to be analyzed.
Required.
May be a GPSS Matrix of up to 6 dimensions of any shape. The argument must be Name.
ReplicateDimension - The dimension of the Result Matrix used for replicates.
Use 0 if there are no replicates. Required. Coerced to integer. The argument
must be Expression.
InteractionLimit - The Limit of Factor Interactions to be analyzed.
This value can be 1, 2, or 3. It is normally used to preserve Degrees of
Freedom for the estimate of the Standard Error instead of using them on an
interaction presumed to be unimportant. Required. Coerced to integer.
The argument must be Expression.

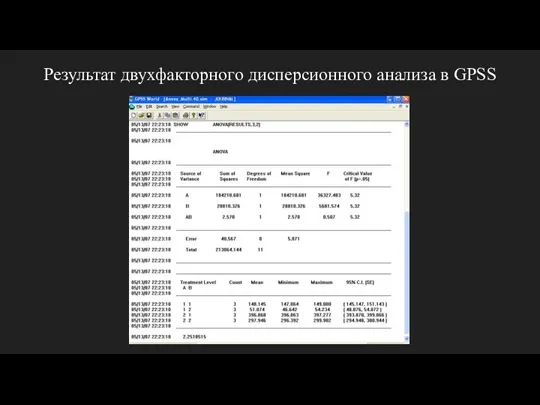
Интерпретация полученных данных
Таблица содержит интерпретацию результатов дисперсионного анализа влияния фактора А. Полученное значение статистики Фишера существенно превышает критическое значение для уровня значимости 5%: F >( F = 7 ,71 ).

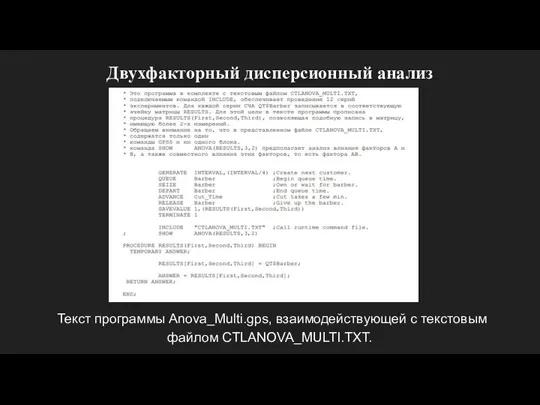
Двухфакторный дисперсионный анализ
Текст программы Anova_Multi.gps, взаимодействующей с текстовым файлом CTLANOVA_MULTI.TXT.

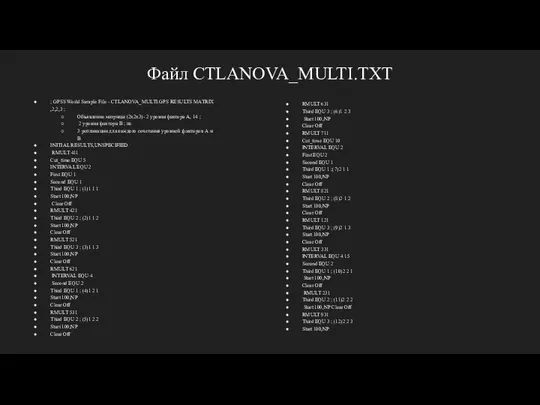
Файл CTLANOVA_MULTI.TXT
; GPSS World Sample File - CTLANOVA_MULTI.GPS RESULTS MATRIX ,2,2,3 ;
Объявление матрицы (2х2x3)- 2 уровня фактора А, 14 ;
2 уровня фактора В ; по
3 репликации для каждого сочетания уровней ;факторов А и В
INITIAL RESULTS,UNSPECIFIED
RMULT 411
Cut_time EQU 5
INTERVAL EQU 2
First EQU 1
Second EQU 1
Third EQU 1 ; (1)1 1 1
Start 100,NP
Clear Off
RMULT 421
Third EQU 2 ; (2)1 1 2
Start 100,NP
Clear Off
RMULT 521
Third EQU 3 ; (3)1 1 3
Start 100,NP
Clear Off
RMULT 621
INTERVAL EQU 4
Second EQU 2
Third EQU 1 ; (4)1 2 1
Start 100,NP
Clear Off
RMULT 531
Third EQU 2 ; (5)1 2 2
Start 100,NP
Clear Off
RMULT 631
Third EQU 3 ; (6)1 2 3
Start 100,NP
Clear Off
RMULT 711
Cut_time EQU 10
INTERVAL EQU 2
First EQU 2
Second EQU 1
Third EQU 1 ;(7)2 1 1
Start 100,NP
Clear Off
RMULT 821
Third EQU 2 ; (8)2 1 2
Start 100,NP
Clear Off
RMULT 121
Third EQU 3 ; (9)2 1 3
Start 100,NP
Clear Off
RMULT 331
INTERVAL EQU 4 15
Second EQU 2
Third EQU 1 ; (10)2 2 1
Start 100,NP
Clear Off
RMULT 231
Third EQU 2 ; (11)2 2 2
Start 100,NP Clear Off
RMULT 931
Third EQU 3 ; (12)2 2 3
Start 100,NP

Результат двухфакторного дисперсионного анализа в GPSS