Содержание
- 2. Проецирование - процесс построения изображения предмета на плоскости при помощи проецирующих лучей. В результате получается изображение,
- 3. Различают проекции в зависимости от положения относительно плоскостей: плоскости общего положения; плоскости частного положения. Комплексный чертеж
- 4. Плоскость общего положения – плоскость (АВС), наклоненная под произвольными углами к плоскостям проекций (рис.1). Рисунок 1
- 5. Плоскости частного положения чаще всего задаются следами. Плоскости частного положения можно разделить на две группы :
- 6. Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (рис.2). Треугольник ABC, лежащий в горизонтальной плоскости
- 7. Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (рис. 3). Треугольник ABC, лежащий во фронтальной
- 8. Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (рис. 4). Треугольник ABC, лежащий в профильной
- 9. Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций П1 (рис.5). Горизонтально-проецирующая плоскость задается горизонтальным следом плоскости
- 10. Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций П2, задается фронтальным следом плоскости ∆2 (рис.6). Проекции
- 11. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций П3 , задается профильным следом плоскости Г3 (рис.
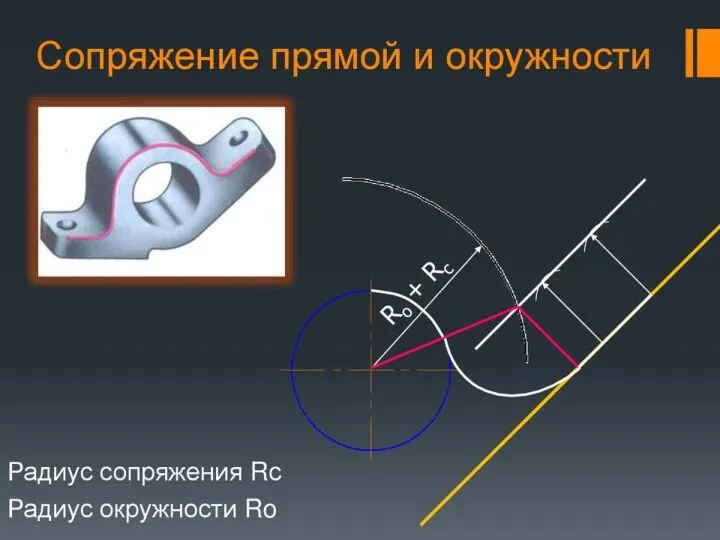
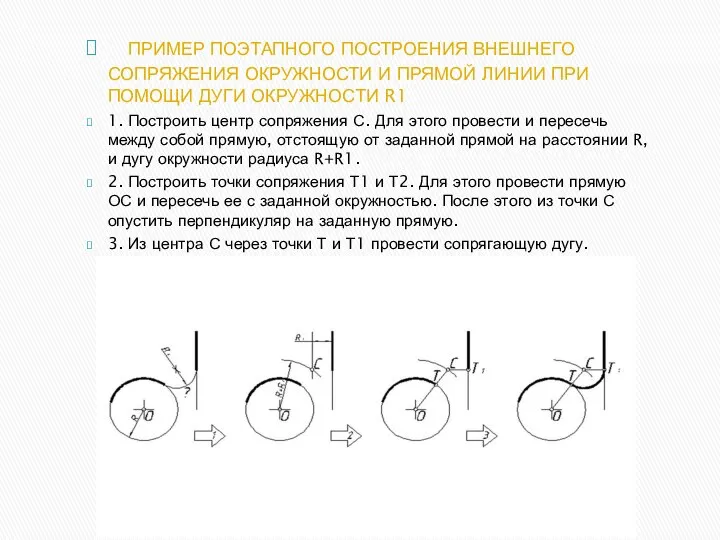
- 20. ПРИМЕР ПОЭТАПНОГО ПОСТРОЕНИЯ ВНЕШНЕГО СОПРЯЖЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ ЛИНИИ ПРИ ПОМОЩИ ДУГИ ОКРУЖНОСТИ R1 1. Построить
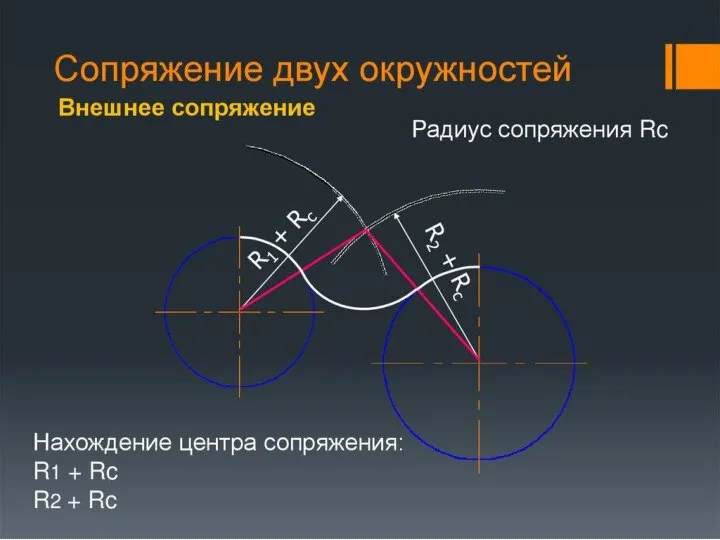
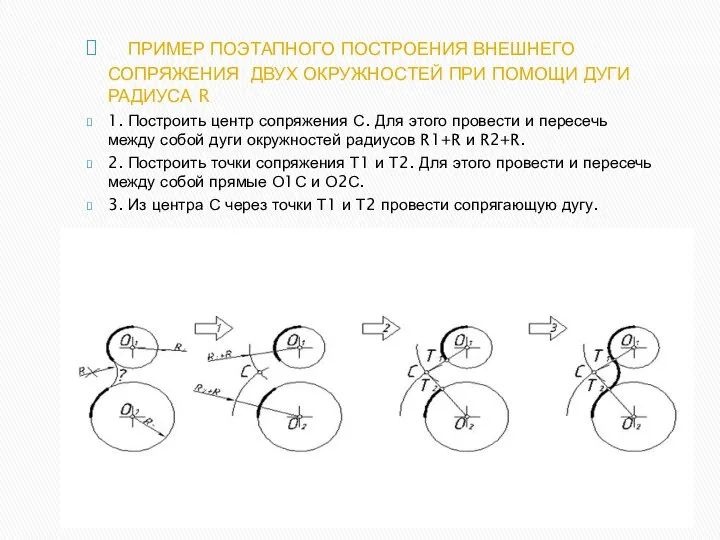
- 22. ПРИМЕР ПОЭТАПНОГО ПОСТРОЕНИЯ ВНЕШНЕГО СОПРЯЖЕНИЯ ДВУХ ОКРУЖНОСТЕЙ ПРИ ПОМОЩИ ДУГИ РАДИУСА R 1. Построить центр сопряжения
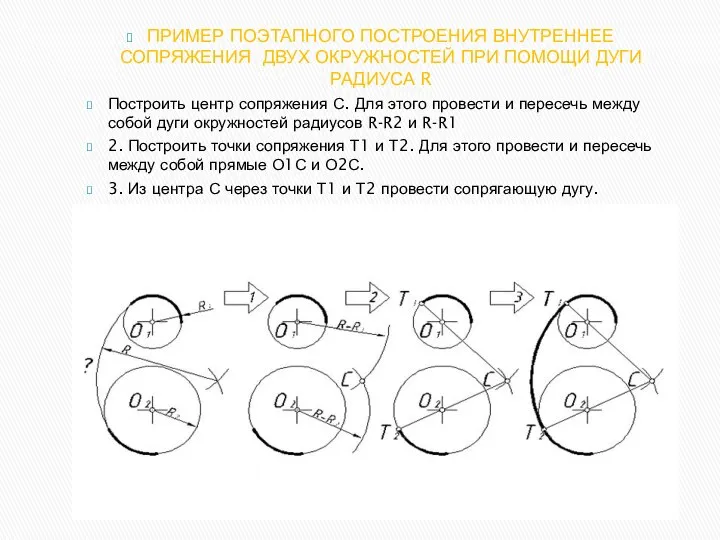
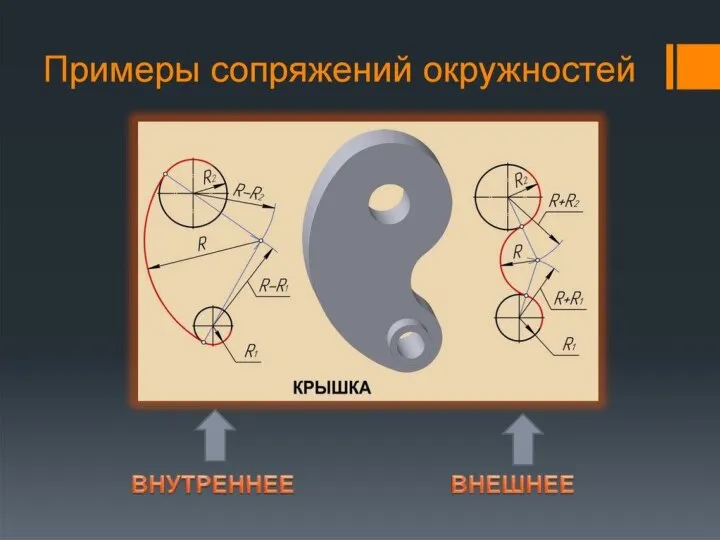
- 24. ПРИМЕР ПОЭТАПНОГО ПОСТРОЕНИЯ ВНУТРЕННЕЕ СОПРЯЖЕНИЯ ДВУХ ОКРУЖНОСТЕЙ ПРИ ПОМОЩИ ДУГИ РАДИУСА R Построить центр сопряжения С.
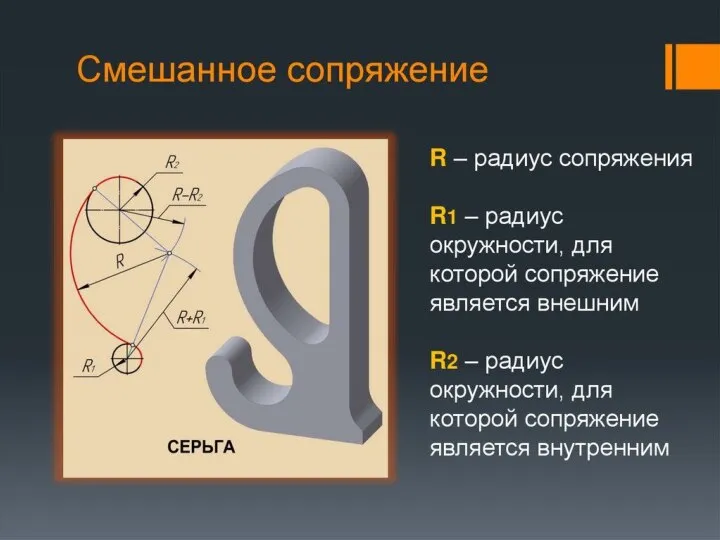
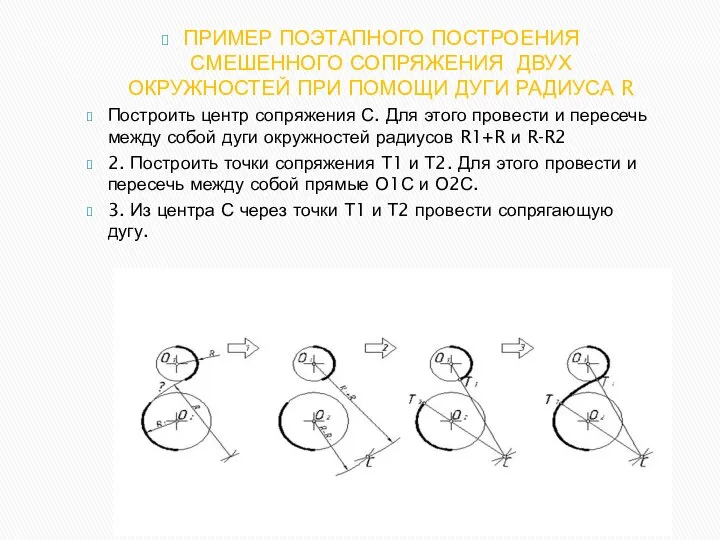
- 27. ПРИМЕР ПОЭТАПНОГО ПОСТРОЕНИЯ СМЕШЕННОГО СОПРЯЖЕНИЯ ДВУХ ОКРУЖНОСТЕЙ ПРИ ПОМОЩИ ДУГИ РАДИУСА R Построить центр сопряжения С.
- 39. Скачать презентацию














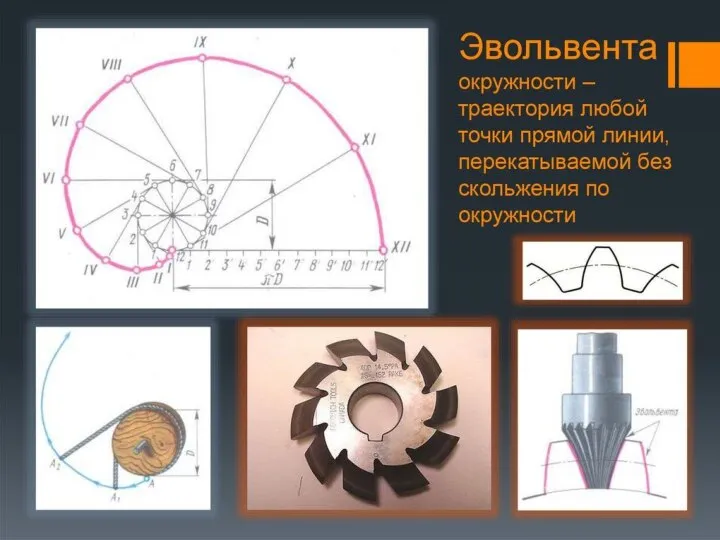
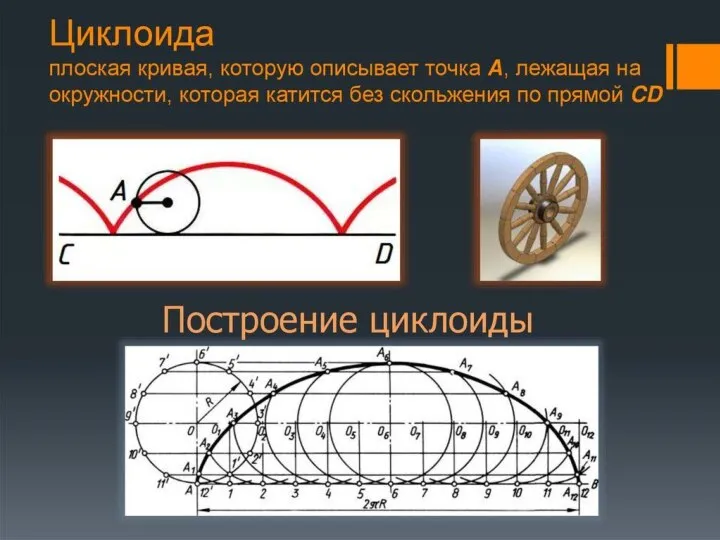
 Обучающий словарный диктант
Обучающий словарный диктант Проблемы колонизации.Солнечной системы
Проблемы колонизации.Солнечной системы Православный календарь
Православный календарь Ростов- город воинской славы
Ростов- город воинской славы Современные способы обработки цветных металлов
Современные способы обработки цветных металлов Презентация на тему Жизнь и деятельность Чарлза Дарвина
Презентация на тему Жизнь и деятельность Чарлза Дарвина  Школа №1195 Дошкольное отделение
Школа №1195 Дошкольное отделение Чем можно и чем не стоит жертвовать в коммуникациях на нерастущих рынках
Чем можно и чем не стоит жертвовать в коммуникациях на нерастущих рынках Молоко и молочные продукты. Исследование качества молока
Молоко и молочные продукты. Исследование качества молока Сергей Иванович Ожегов
Сергей Иванович Ожегов Поэзия повседневной жизни в искусстве разных народов
Поэзия повседневной жизни в искусстве разных народов Классификации моделей. Классификации моделей...
Классификации моделей. Классификации моделей... Организационно-правовые формы социального обеспечения
Организационно-правовые формы социального обеспечения Ivideon ANPR. Распознавание автомобильных номеров
Ivideon ANPR. Распознавание автомобильных номеров Отчет по площадке Сентябрь 2011
Отчет по площадке Сентябрь 2011 Социальная психология. Практическая работа
Социальная психология. Практическая работа Тюлегенова Шахида Мубаракшаевнаучитель истории, обществознания и права МОУ СОШ № 5 г. Соль-ИлецкаОбразование: высшее, ОГПИ, 1990 г.С
Тюлегенова Шахида Мубаракшаевнаучитель истории, обществознания и права МОУ СОШ № 5 г. Соль-ИлецкаОбразование: высшее, ОГПИ, 1990 г.С Презентация на тему Преодоление отсталости развивающихся стран
Презентация на тему Преодоление отсталости развивающихся стран  Политическая система. Субъекты государственной власти РФ
Политическая система. Субъекты государственной власти РФ Отчёт о деятельности секции фониатров Российского общества оториноларингологов за период с 2007 по 2008 гг.
Отчёт о деятельности секции фониатров Российского общества оториноларингологов за период с 2007 по 2008 гг. Двери новой конструкции ДС 2
Двери новой конструкции ДС 2 Электрические станции на службе у человека
Электрические станции на службе у человека Презентация на тему Непроизносимые согласные в корне слова
Презентация на тему Непроизносимые согласные в корне слова  Презентация на темум Мусор и как с ним бороться
Презентация на темум Мусор и как с ним бороться Введение в Интернет
Введение в Интернет Психическое здоровье в условиях пандемии
Психическое здоровье в условиях пандемии Интерактивная выставка-презентация Финансы России: время первых (II этап)
Интерактивная выставка-презентация Финансы России: время первых (II этап) Презентация на тему Антон Павлович Чехов «Дядя Ваня»
Презентация на тему Антон Павлович Чехов «Дядя Ваня»