Содержание
- 2. Математика с её строгими рассуждениями и доказательствами предлагает физике ясную форму, которая помогает нашим размышлениям. При
- 3. Одно и то же уравнение для функции у(x) описывает одновременно множество физических объектов; y(x) может означать
- 4. Наука о природе зародилась в древнегреческой философии две с половиной тысячи лет назад. Архимед ввёл понятие
- 5. Языком величин формулируются физические законы и теории. Связи величин, их взаимозависимость выражаются с помощью формул. Величины
- 6. Абсолютная погрешность приближённого значения величины – это модуль разности точного и приближённого значений величины, зависит от
- 7. Относительная погрешность приближённого значения величины – это отношение абсолютной погрешности к модулю приближённого значения; характеризует качество
- 8. Ещё пример. С какой абсолютной погрешностью следует измерить объём воды в измерительном цилиндре, чтобы относительная погрешность
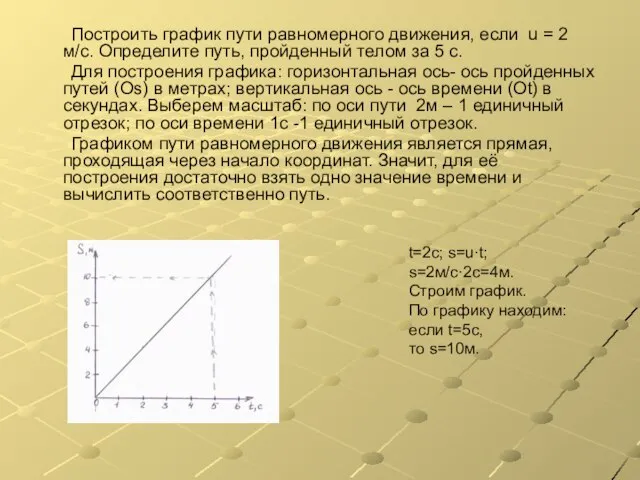
- 9. Построить график пути равномерного движения, если u = 2 м/с. Определите путь, пройденный телом за 5
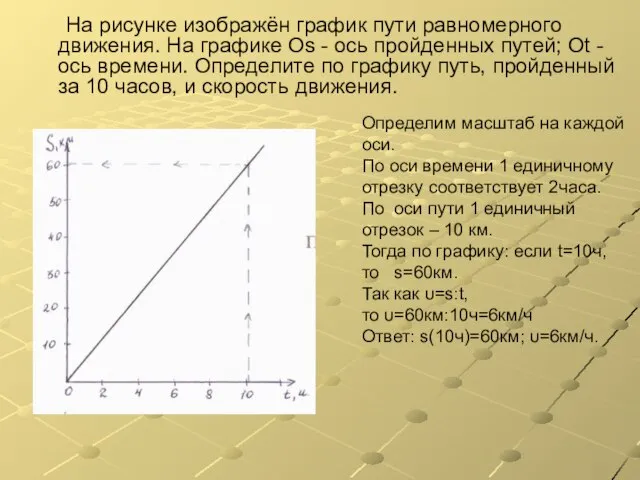
- 10. На рисунке изображён график пути равномерного движения. На графике Оs - ось пройденных путей; Оt -
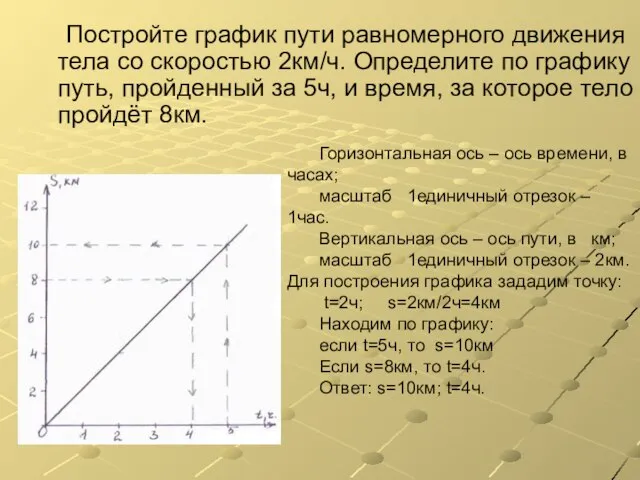
- 11. Постройте график пути равномерного движения тела со скоростью 2км/ч. Определите по графику путь, пройденный за 5ч,
- 14. 1) 2)
- 17. Скачать презентацию











 Вводные слова и предложения, правила их обозначения
Вводные слова и предложения, правила их обозначения Такие разные Жесты
Такие разные Жесты Инновационные образовательные методы и технологии
Инновационные образовательные методы и технологии Бури, смерчи, ураганы
Бури, смерчи, ураганы Сказка
Сказка Основные методы регулирования международной трудовой миграции
Основные методы регулирования международной трудовой миграции Жизненные ценности героев рассказа А.И.Куприна «Белый пудель»
Жизненные ценности героев рассказа А.И.Куприна «Белый пудель» Сложение и вычитание натуральных чисел и его свойства
Сложение и вычитание натуральных чисел и его свойства Краши Катерины Гурлебаус
Краши Катерины Гурлебаус Финансы и финансовое право
Финансы и финансовое право Основы законодательства об информации и её защите
Основы законодательства об информации и её защите Горох Менделя
Горох Менделя Библиотечный кукольный театр Рыжий Кот
Библиотечный кукольный театр Рыжий Кот Республиканский конкурс Женщина-мать нации 2021
Республиканский конкурс Женщина-мать нации 2021 Презентация на тему Животноводство Окружающий мир - 3 класс
Презентация на тему Животноводство Окружающий мир - 3 класс  Гиподинамия – малоподвижный образ жизни. Почему возникла эта проблема в 21 веке?
Гиподинамия – малоподвижный образ жизни. Почему возникла эта проблема в 21 веке? Єдиний державний реєстр юридичних осіб, фізичних осіб підприємців та громадських формувань
Єдиний державний реєстр юридичних осіб, фізичних осіб підприємців та громадських формувань Проектирование баз данных
Проектирование баз данных Презентация на тему "Переход от игровой деятельности к учебной как основа создания комфортных условий для обучения" - скачать
Презентация на тему "Переход от игровой деятельности к учебной как основа создания комфортных условий для обучения" - скачать Финансовая грамотность
Финансовая грамотность Аргаяшский аграрный техникум. Конкурсные задания олимпиады профмастерства студентов
Аргаяшский аграрный техникум. Конкурсные задания олимпиады профмастерства студентов Омские храмы, связанные с именем Сильвестра Ольшевского
Омские храмы, связанные с именем Сильвестра Ольшевского Башнефтегеофизика
Башнефтегеофизика Сказочно - былинный жанр
Сказочно - былинный жанр Шок в клинике внутренних болезней
Шок в клинике внутренних болезней Воспитательный компонент Федерального государственного стандарта
Воспитательный компонент Федерального государственного стандарта Формирование основ здорового образа жизни
Формирование основ здорового образа жизни Географические названия Великобритании
Географические названия Великобритании