Содержание
- 2. Отыскание наибольшего и наименьшего значений непрерывной функции на промежутке
- 3. Например: . Построив ее график у наим.=-1\2, а у наиб.= 1\2 у х О 1 -1
- 4. Можно рассуждать так Значит yнаиб=3 С другой стороны Значит унаим.=0 Можно находить наименьшее и наибольшее значение
- 5. Пусть y=f(х) непрерывна на отрезке [a, b] Например: а b Yнаим. Yнаиб.. Yнаим. Yнаиб.. а b
- 6. 1. Если функция непрерывна на отрезке, то она достигает на нем и своего наибольшего и своего
- 7. Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции y=f(х) на отрезке [a, b]. Найти производную f\(x)
- 8. Пример 1: А) на отрезке [-4, 6] Б) на отрезке [0, 6] В) на отрезке [-2,
- 9. а) х=-3 и х=5 принадлежат заданному [-4, 6] Составим таблицу значений функции Таким образом унаим.=-174 (достигается
- 10. б) х=5 принадлежит [0, 6] Составим таблицу значений функции Таким образом, унаим.=-174 (достигается в точке х=5);
- 11. в) Отрезку [-2, 2] не принадлежит ни одна из найденных стационарных точек f(-2)=71 f(2)= -93 Таким
- 12. Пример 2:
- 15. Составим таблицу значений функции Ответ: унаим.= -3/25; унаиб.= 38
- 16. Теорема: Пусть функция у=f(x) непрерывна на промежутке Х и имеет внутри него единственную стационарную или критическую
- 17. 0 0 y x y x a b a b унаим. унаим.
- 19. Скачать презентацию



![Пусть y=f(х) непрерывна на отрезке [a, b] Например: а b Yнаим. Yнаиб..](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/394373/slide-4.jpg)


![Пример 1: А) на отрезке [-4, 6] Б) на отрезке [0, 6]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/394373/slide-7.jpg)
![а) х=-3 и х=5 принадлежат заданному [-4, 6] Составим таблицу значений функции](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/394373/slide-8.jpg)
![б) х=5 принадлежит [0, 6] Составим таблицу значений функции Таким образом, унаим.=-174](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/394373/slide-9.jpg)
![в) Отрезку [-2, 2] не принадлежит ни одна из найденных стационарных точек](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/394373/slide-10.jpg)





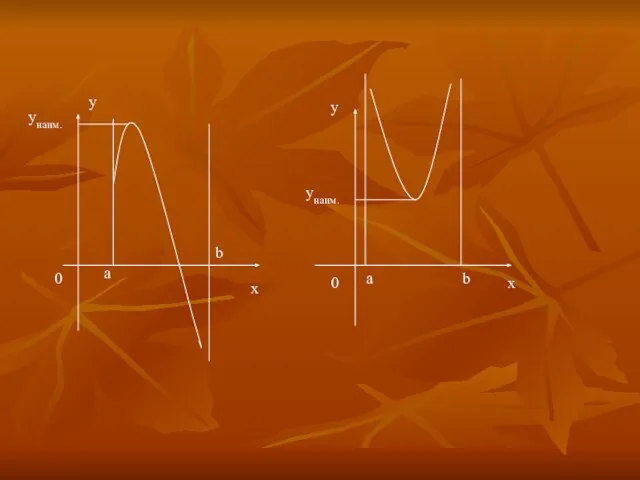
 Характеристика стран восточной Европы
Характеристика стран восточной Европы Правительство Москвы
Правительство Москвы Психолого – педагогическая служба в образовательном процессе
Психолого – педагогическая служба в образовательном процессе Стандарты кредитной надежности
Стандарты кредитной надежности Методика оценки командной эффективности. Социальные драйверы командной эффективности
Методика оценки командной эффективности. Социальные драйверы командной эффективности T-fest
T-fest Студенты-гуманитарии и вытеснение “систематического” мышления “поисковым”:к постановке проблемы
Студенты-гуманитарии и вытеснение “систематического” мышления “поисковым”:к постановке проблемы Презентация на тему Страны Африки. Ливия
Презентация на тему Страны Африки. Ливия  Проведение недель профессионального мастерства как форма коллективной методической работы
Проведение недель профессионального мастерства как форма коллективной методической работы  OpenOffice.org Writer
OpenOffice.org Writer GK120产品保养调整介绍
GK120产品保养调整介绍 Таргетированная реклама
Таргетированная реклама Musical Crossword
Musical Crossword Работа с контурной картой возраст гор
Работа с контурной картой возраст гор Учимся рисовать гуашью букет подсолнухов
Учимся рисовать гуашью букет подсолнухов ВИДЫ ТЕПЛОПЕРЕДАЧИ
ВИДЫ ТЕПЛОПЕРЕДАЧИ 23 февраля День защитника Отечества
23 февраля День защитника Отечества Растения Красной книги
Растения Красной книги Интегрированный урок в начальной школе
Интегрированный урок в начальной школе Курск Малая родина моя
Курск Малая родина моя Organic therapy
Organic therapy Приходи в Диснейленд
Приходи в Диснейленд אנחנו רוצים מחברות חדשות
אנחנו רוצים מחברות חדשות Христианская семья
Христианская семья Изготовление ящика для инструментов
Изготовление ящика для инструментов Воспитательный потенциал семьи
Воспитательный потенциал семьи Приходи на ФПММ — у нас интересно!
Приходи на ФПММ — у нас интересно! Биография Ф. И. Тютчева
Биография Ф. И. Тютчева