Содержание
- 2. Великий французский математик Пьер Ферма в 1629 году научился находить касательные к алгебраическим прямым. Как родилась
- 3. Как родилась производная Тем не менее, выдвинутые идеи не пропали впустую. Многие из них легли в
- 4. Как родилась производная Очень многие великие ученые внесли свой вклад в зарождение и развитие дифференциального исчисления
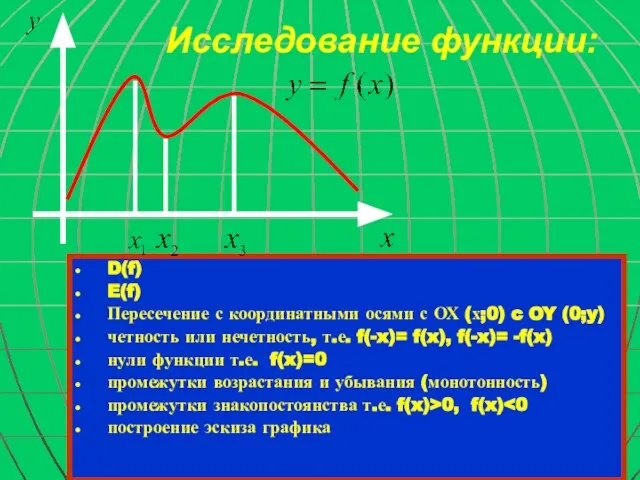
- 5. Исследование функции: D(f) E(f) Пересечение с координатными осями с ОХ (х;0) c OY (0;y) четность или
- 6. Четность, нечетность функций Периодичность Нули функции Промежутки знакопостоянства Монотонность функции Повторение далее
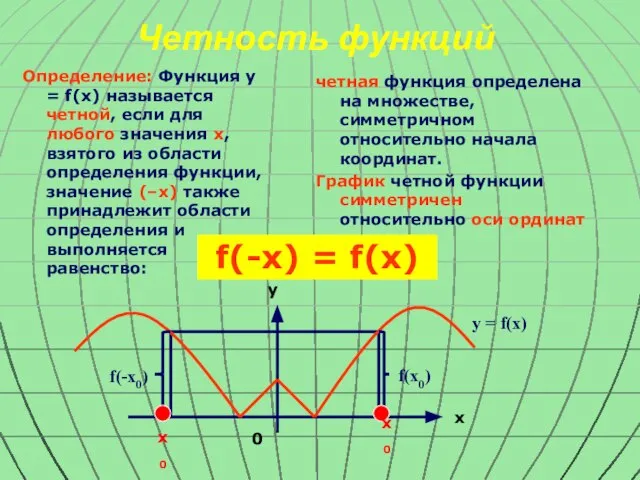
- 7. Четность функций Определение: Функция y = f(x) называется четной, если для любого значения x, взятого из
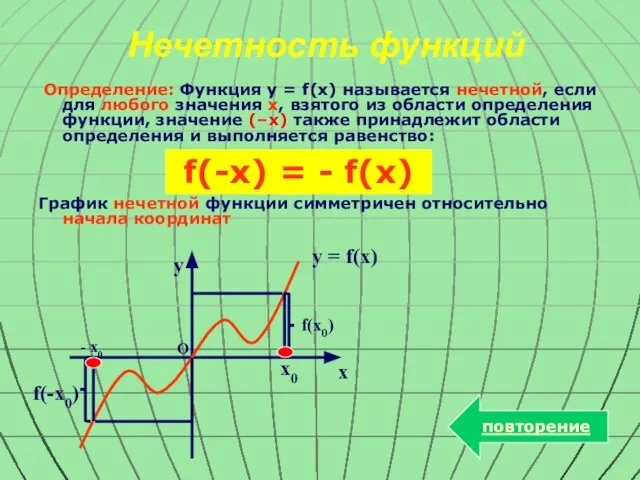
- 8. f(-x0) O y = f(x) Нечетность функций Определение: Функция y = f(x) называется нечетной, если для
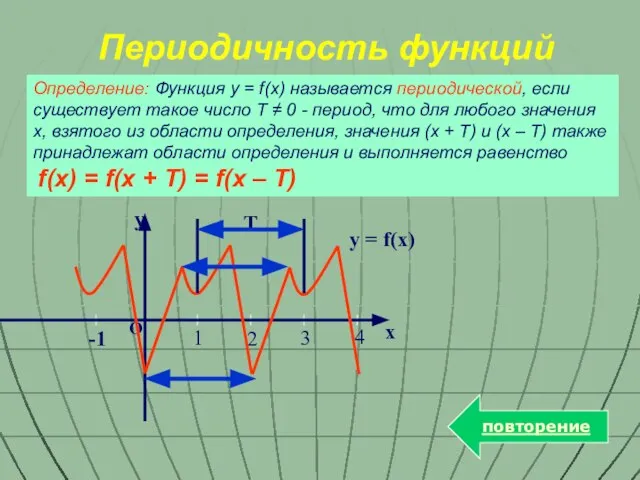
- 9. Определение: Функция y = f(x) называется периодической, если существует такое число T ≠ 0 - период,
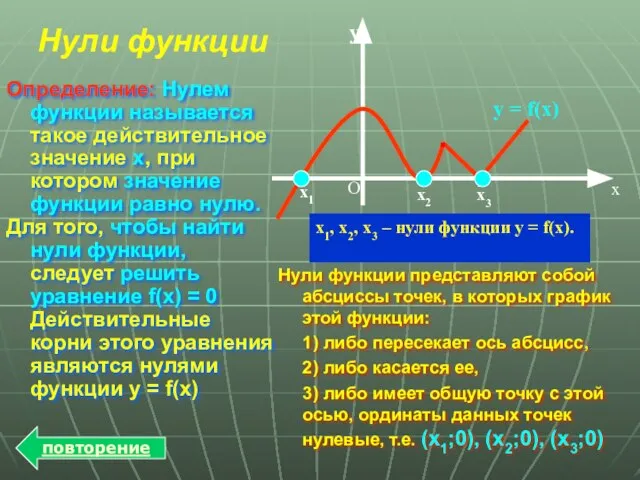
- 10. х1, х2, х3 – нули функции у = f(x). Нули функции Определение: Нулем функции называется такое
- 11. Промежутки знакопостоянства Определение: Числовые промежутки, на которых непрерывная функция сохраняет свой знак и не обращается в
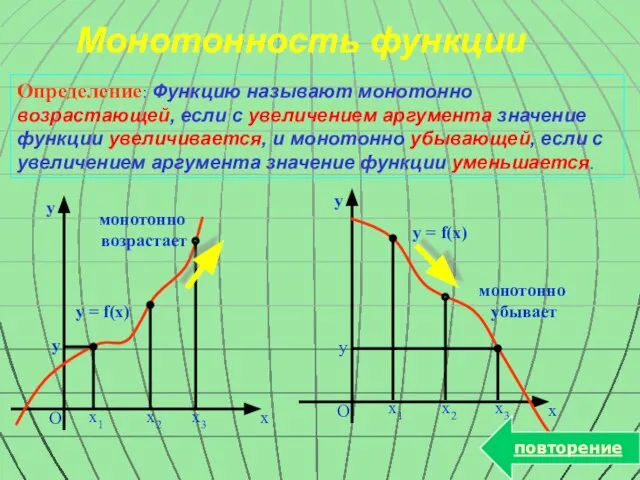
- 12. Монотонность функции Определение: Функцию называют монотонно возрастающей, если с увеличением аргумента значение функции увеличивается, и монотонно
- 13. Если производная функции в каждой точке некоторого промежутка положительна, то функция на этом промежутке возрастает, т.е.f’(x)>0,
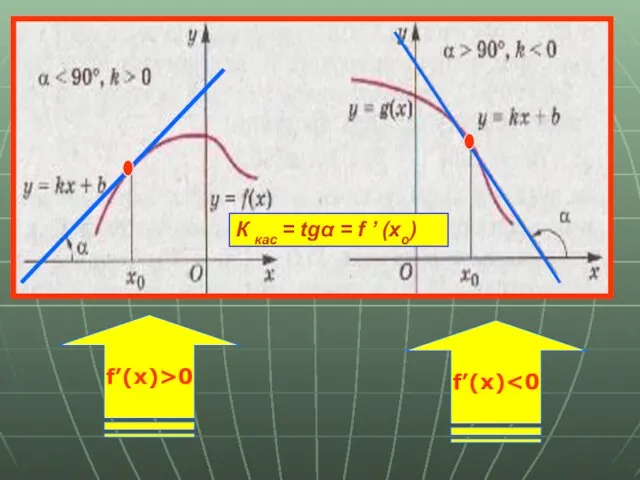
- 14. f’(x)>0 f’(x) К кас = tgα = f ’ (xo)
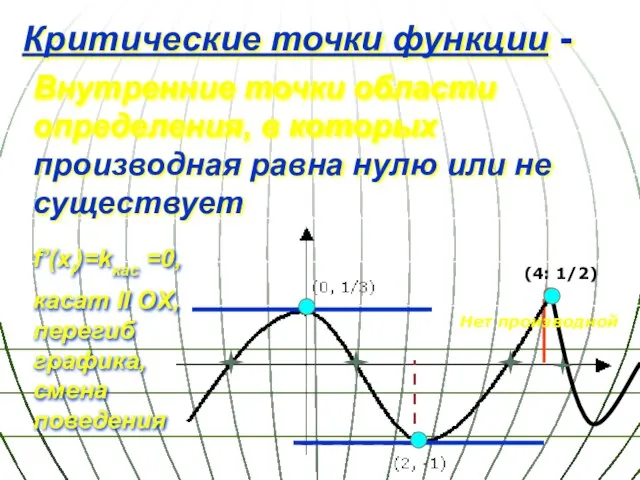
- 15. Внутренние точки области определения, в которых производная равна нулю или не существует Критические точки функции -
- 16. критические точки Достаточный признак возрастания или убывания функции Пример: Найти промежутки возрастания и убывания функции f(x)=х3
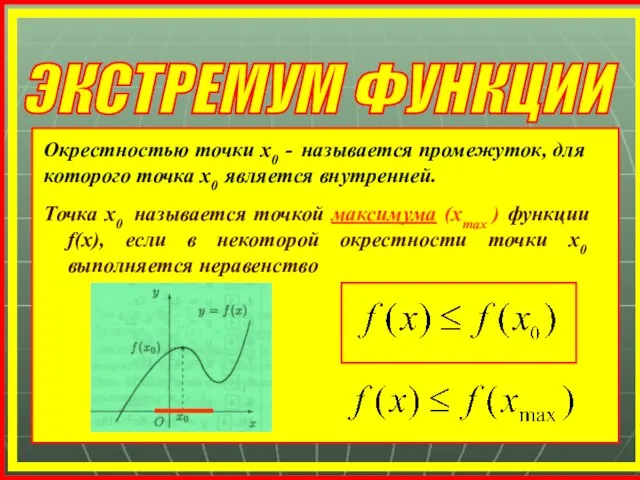
- 17. ЭКСТРЕМУМ ФУНКЦИИ Точка х0 называется точкой максимума (xmax ) функции f(x), если в некоторой окрестности точки
- 18. Точка х1 называется точкой минимума (xmin ) функции f(x), если в некоторой окрестности точки х1 выполняется
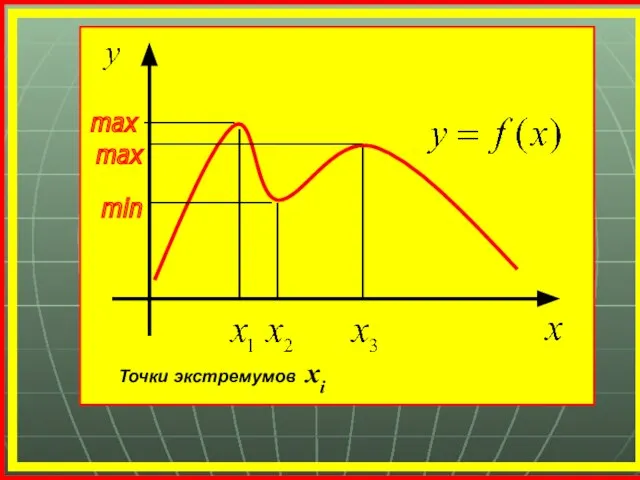
- 19. max min max Точки экстремумов хі
- 20. Обратите внимание!!! Что происходит с производной при переходе через экстремальную точку? Что происходит с самой функцией
- 21. Достаточный признак возрастания или убывания функции Если производная функции в каждой точке некоторого промежутка положительна, то
- 22. Необходимое условие существования экстремума: Точками экстремума функции могут быть только её критические точки (в которых производная
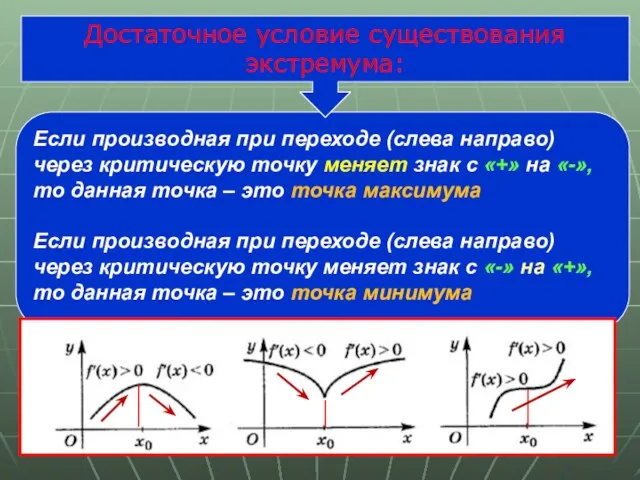
- 23. Если производная при переходе (слева направо) через критическую точку меняет знак с «+» на «-», то
- 25. Найти точки экстремумов функции: Решение различных типов задач
- 26. Найти точки экстремумов функции и экстремальные значения:
- 28. Найти промежутки убывания и возрастания функции:
- 29. Найти критические точки функции:
- 32. Скачать презентацию


















 Паспорт объекта сети Харьковская региональная дирекция
Паспорт объекта сети Харьковская региональная дирекция Презентация на тему Средства для борьбы с насекомыми
Презентация на тему Средства для борьбы с насекомыми Задачи и методы современной психологии
Задачи и методы современной психологии Подходы к моделированию ГРА
Подходы к моделированию ГРА Технология продуктивного чтения или формирование типа правильной читательской деятельности
Технология продуктивного чтения или формирование типа правильной читательской деятельности Заработать в интернете без вложений и без продаж
Заработать в интернете без вложений и без продаж Понятие стратегического менеджмента
Понятие стратегического менеджмента Ультразвуковой уровнемер на микроконтроллере PIC16F628
Ультразвуковой уровнемер на микроконтроллере PIC16F628 Роза из бумаги
Роза из бумаги ОАО «Противокарстовая и береговая защита» 606019, Нижегородская обл., г.Дзержинск, ул.Гастелло, 10/15 Тел./факс (8313) 25-98-01 E-mail:
ОАО «Противокарстовая и береговая защита» 606019, Нижегородская обл., г.Дзержинск, ул.Гастелло, 10/15 Тел./факс (8313) 25-98-01 E-mail:  Готовимся к части С
Готовимся к части С EBG Customer Training Map
EBG Customer Training Map Виды и назначение технологических карт
Виды и назначение технологических карт Учредитель: Администрация Городского округа «Город Волжск». Адрес:425000, ул. Коммунистическая, д.1.
Учредитель: Администрация Городского округа «Город Волжск». Адрес:425000, ул. Коммунистическая, д.1. Презентация на тему Русь и Золотая Орда (6 класс)
Презентация на тему Русь и Золотая Орда (6 класс) Анализ системы подготовки и аттестации кадров предприятия туризма. Задание 5
Анализ системы подготовки и аттестации кадров предприятия туризма. Задание 5 Нетрадиционная техника рисования граттаж Праздничный салют
Нетрадиционная техника рисования граттаж Праздничный салют сочинение
сочинение Проект « Профессии наших родителей»
Проект « Профессии наших родителей» Натюрморт
Натюрморт Ц у н а м и
Ц у н а м и Публичная презентация результатов педагогической деятельностии инновационной работыучителя начальных классов МКОУ «Лицей се
Публичная презентация результатов педагогической деятельностии инновационной работыучителя начальных классов МКОУ «Лицей се Психологический климат в семье (8 класс)
Психологический климат в семье (8 класс) Игры с залом PowerPoint
Игры с залом PowerPoint Кулинарный поединок
Кулинарный поединок Food rap
Food rap ЗУП КОРП: реализованная функциональность и выпуск конфигурации Докладчик: Лохтин Т.О.
ЗУП КОРП: реализованная функциональность и выпуск конфигурации Докладчик: Лохтин Т.О. Правила судейства игры Баскетбол
Правила судейства игры Баскетбол