Содержание
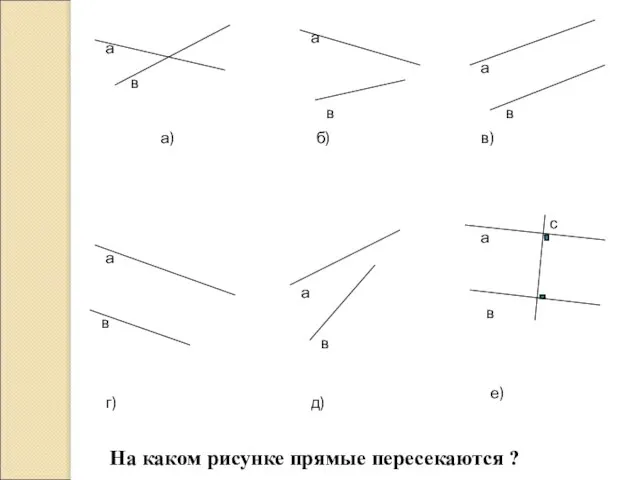
- 2. а в а) а в б) а в в) а в г) а в д) а
- 3. Пересекающиеся прямые имеют: а) не имеют общих точек; б) одну общую точку.
- 4. а в а) а в б) а в в) а в г) а в д) а
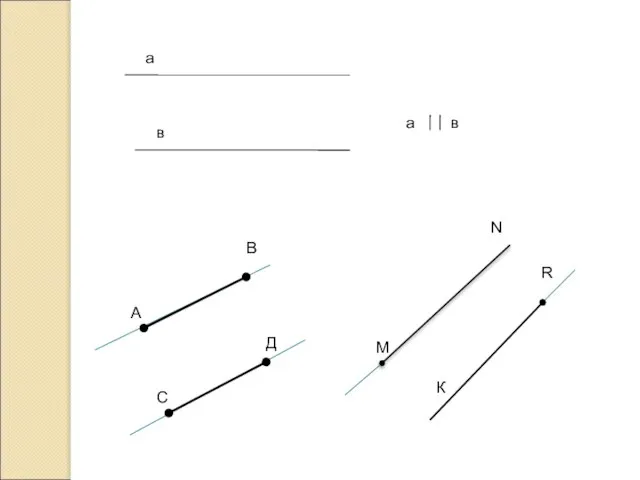
- 5. Две прямые на плоскости называются параллельными: а) если они не пересекаются; б) если они пересекаются.
- 6. а в а в А В С Д М N К R
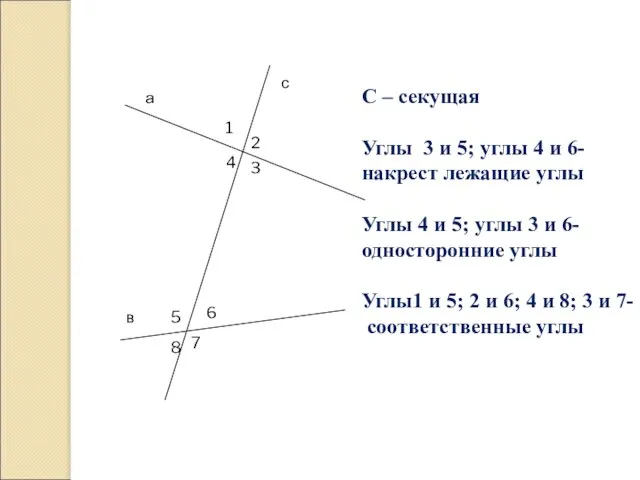
- 7. а в с 1 2 4 3 5 6 8 7 С – секущая Углы 3
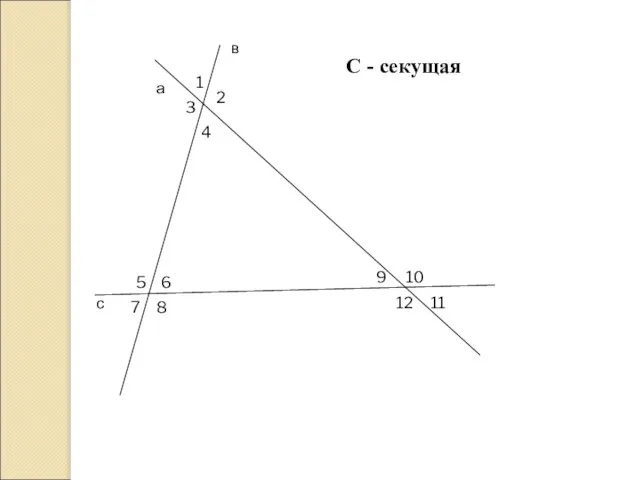
- 8. С - секущая а в с 1 2 3 4 5 6 7 8 9 10
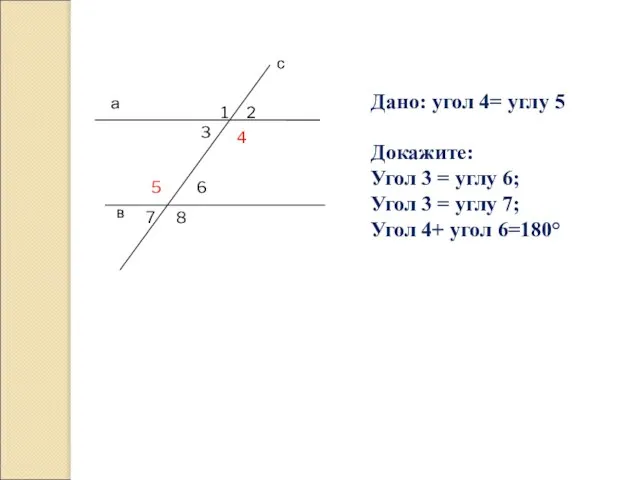
- 9. а в с 1 2 3 4 5 6 7 8 Дано: угол 4= углу 5
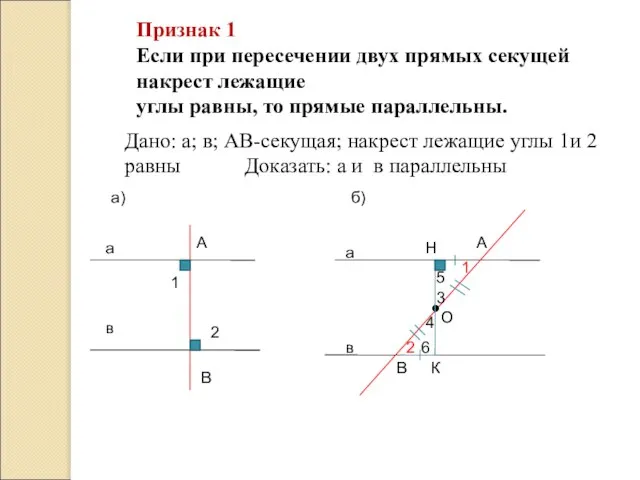
- 10. Признак 1 Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. а
- 11. Признак 2 Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Признак 3
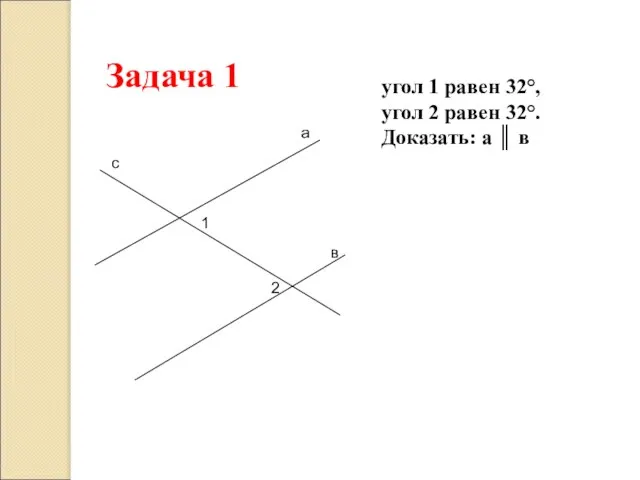
- 12. а в с 1 2 Задача 1 угол 1 равен 32°, угол 2 равен 32°. Доказать:
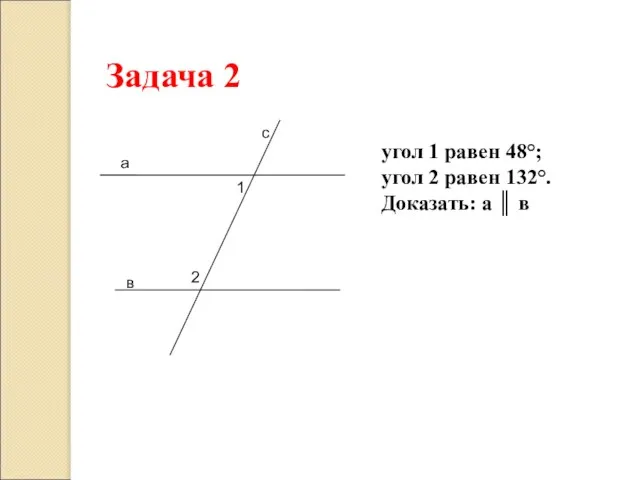
- 13. Задача 2 а в с 1 2 угол 1 равен 48°; угол 2 равен 132°. Доказать:
- 15. Скачать презентацию




 Компьютер и здоровье глаз
Компьютер и здоровье глаз Пейзаж.Времена года
Пейзаж.Времена года Организационное и информационное обеспечение фандрейзинга
Организационное и информационное обеспечение фандрейзинга Сложноподчиненное предложение. Повторение и обобщение изученного.
Сложноподчиненное предложение. Повторение и обобщение изученного. История радио и мобильной связи
История радио и мобильной связи А как ты знаешь физику?
А как ты знаешь физику? Презентация на тему Нефтяная промышленность
Презентация на тему Нефтяная промышленность  Изобразительное искусство барокко
Изобразительное искусство барокко Как начать бизнес в интернете?
Как начать бизнес в интернете? Sony Ericsson: Из VGA в HD
Sony Ericsson: Из VGA в HD Символика Краснодарского края
Символика Краснодарского края Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить.
Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить. Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020
Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020 Children's behavior and its influence on their future acts
Children's behavior and its influence on their future acts РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС
РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС Слова-паразиты, или экология речи
Слова-паразиты, или экология речи Иммунная система и канцерогенез
Иммунная система и канцерогенез  Подарки AI Journey. Предложения. Сберклауд
Подарки AI Journey. Предложения. Сберклауд Философские теории неврозов
Философские теории неврозов Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel)
Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel) Деструктивность учащегося и образовательной среды: точки соприкосновения
Деструктивность учащегося и образовательной среды: точки соприкосновения БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ
БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ Подготовка граждан к военной службе
Подготовка граждан к военной службе Ультразвуковые накладные расходомеры Flexim
Ультразвуковые накладные расходомеры Flexim Презентация для заказных проектов
Презентация для заказных проектов Поступление на государственную службу
Поступление на государственную службу Оценка достижений учащихся в разновозрастной группе
Оценка достижений учащихся в разновозрастной группе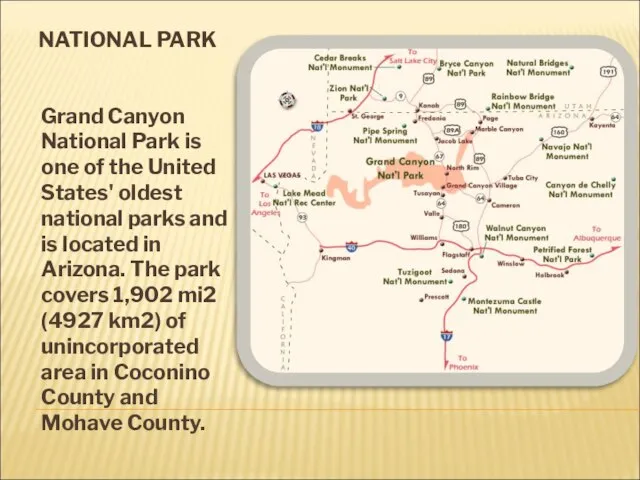 Grand Canyon National Park
Grand Canyon National Park