Продольные и поперечные деформации, закон Гука

Продольная сила. Гипотеза плоских сечений.
Нормальные напряжения в поперечныx
сеченияx бруса.
Центральным растяжением или
сжатием называется такой вид деформации,
при котором в любом поперечном сечении
бруса возникает только продольная
(нормальная) сила N, а все остальные силовые
факторы равны 0. В случае растяжения
продольную силу N будем считать
положительной, при сжатии – отрицательной.
Изменение продольной силы по длине стержня
удобно представить в виде диаграммы, которая
называется эпюрой продольныx сил.

ПРИМЕР №1.
Стержень закреплен одним концом
и нагружен приложенными
вдоль оси силами.
Построить эпюру продольных
сил для этого стержня.
РЕШЕНИЕ:
В защемлённом сечении
возникают реакции Н,
которые можно определить
из уравнения равновесия.

Разделим стержень
на участки, границы
приложения внешних сил.
Пользуясь методом сечений,
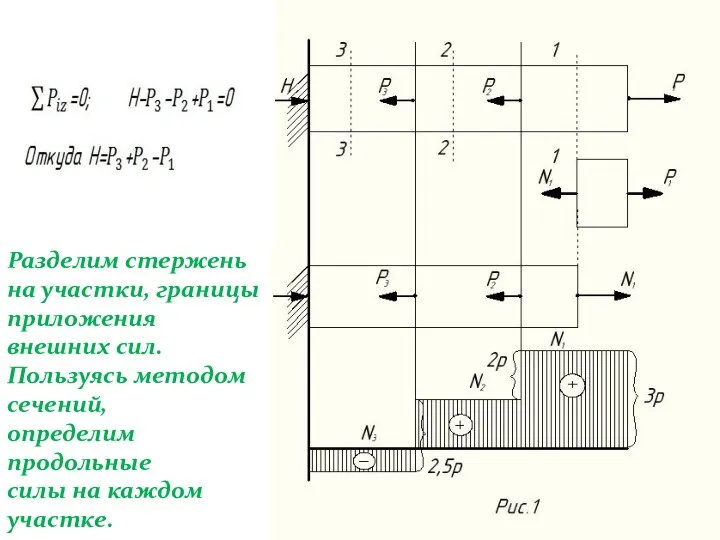
определим продольные
силы на каждом участке.

Нормальное напряжение в поперечныx сеченияx бруса.
На основании гипотез Бернулли
можно заключить, что все точки
какого-либо поперечного стержня
находятся в одинаковых условиях, и,
условно, напряжения распределяются
по сечению равномерно. Эти напряжения параллельны продольной силе, т.е перпендикулярны поперечному сечению, а значит являются нормальными напряжениями.

Для большинства
конструктивныx
материалов существует
прямо пропорциональная
зависимость. Приведенная
зависимость называется
законом Гука (английский
физик 1660 г.) и является основным
законом сопротивления материалов.

Линейная деформация прямо
пропорциональна
соответствующему
нормальному напряжению.
Е – модуль продольной упругости
– одна из важнейших физических
постоянных в материале. Она
характеризует его жесткость,
т.е способность сопротивляться
упругому деформированию
(такие называют модулем Юнга.)

Закон Гука в графической форме δпц–предел пропорциональности.Перемещением поперечного
сечения бруса наз. изменение
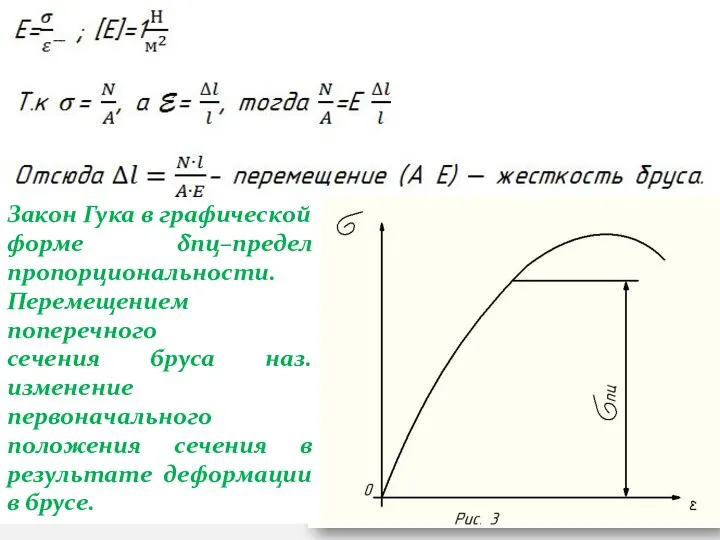
первоначального положения сечения в результате деформации в брусе.

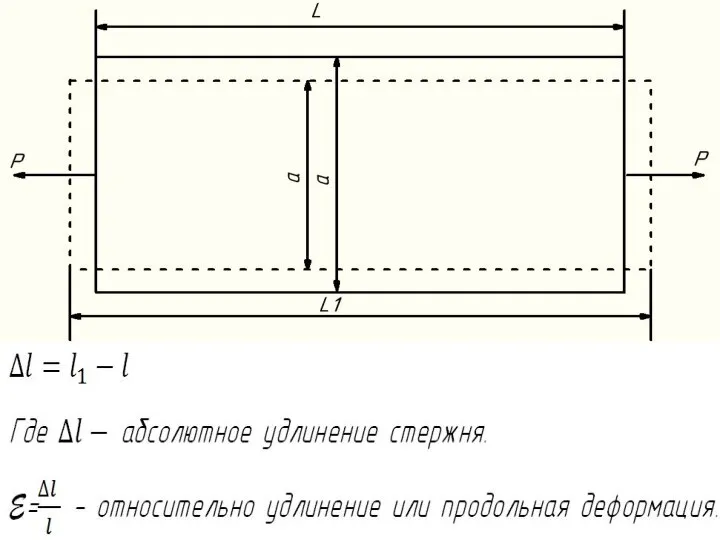
3. Жесткость сечения бруса при
растяжении и сжатии.
Поперечная деформация.
Коэффициент Пуассона