Проект Казино – шанс или обман

Паспорт проекта
Цель исследования:
Углубление в такие разделы математики как теория игр, комбинаторика, теория вероятности на примере азартных игр.
Задачи исследования:
Изучение соответствующих разделов математики (комбинаторика, теория вероятности, теория игр).
Изучение вероятности и коэффициентов выигрышей на основе казино и лотереи.
Анализ шансов на успешную игру и подведение итоговой оценки этому методу заработка.
Разработка и проведение мини-игры по типу лотереи.
Нахождение дополнительных применений теории игр, комбинаторике и теории вероятности.

Гипотеза:
Вне зависимости от удачи, смысла пытаться обогатиться таким способом, нет.
Продукт проекта: анкетирование учащихся девятых классов на тему азартных игр
Актуальность:
Простота азартных игр так и тянет опробовать их. Однако люди все проигрывают и проигрывают свои кровно заработанные. И ведь кого-то это не останавливает: «Им не повезло, но я особенный». Но этот проект попробует объективно разобраться в возможности заработка таким путем.

Создатели
Джон фон Нейман
Оскар Моргенштерн

Введение в теорию игр
Игра – процесс, в котором участвуют две или более сторон, ведущих борьбу за реализацию своих интересов.
Теория игр — это раздел математической экономики, изучающий различные игры с точки зрения нахождения оптимальной стратегии и тактики.

Одна задача об односторонней ладье

Рулетка

Математическое ожидание
- формула математического ожидания, где x – событие, p – вероятность этого события.
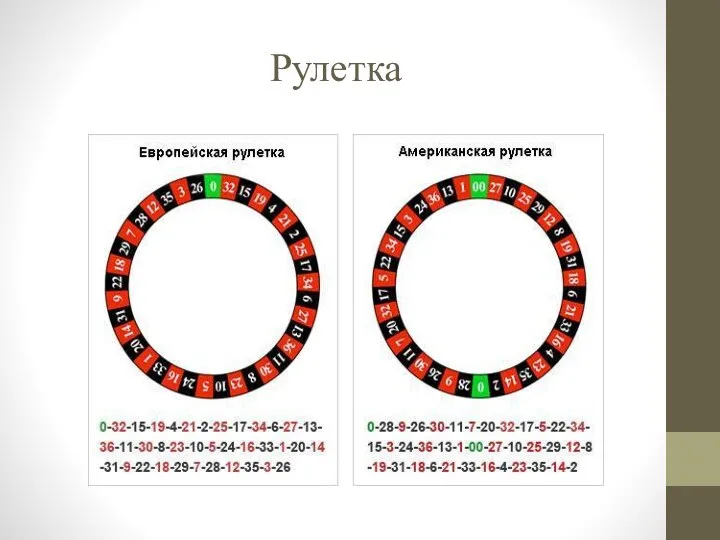
Для стандартной рулетки математическое ожидание рассчитывается как M(X) =18/37 + (-19/37) = -1/37