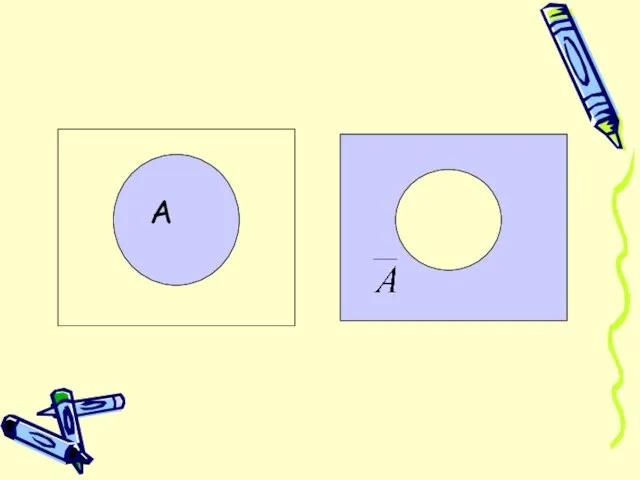
Слайд 2Событие
противоположное
событию А,
обозначают .

Слайд 3Пример: Бросают игральную кость . Рассмотрим событие А «выпало число, большее 4».

Слайд 4Р(А)+Р( )=1
Сумма вероятностей
взаимно противоположных
событий равна единице.

Слайд 5Задания.
1.В некотором случайном опыте может произойти событие А. Найдите вероятность события ,

если вероятность события А равна:
А)0,4 Б) 0,85 В) 0,13 Г)р
2.Докажите , что события А и В не могут быть противоположными , если Р(А)=0,7 Р(В)=0,44.
3.Могут ли быть противоположными событиями А и В, если
А) Р(А)=0,12 Р(В)=0,78.
Б) Р(А)=0,86 Р(В)=0,14.
В) Р(А)=0,5+р Р(В)=0,5-р.
Г) Р(А)= Р(В)=
Слайд 6Соотношения и связи между
событиями можно изобразить
с помощью схематических
рисунков. Такие рисунки
называются диаграммами
Эйлера.

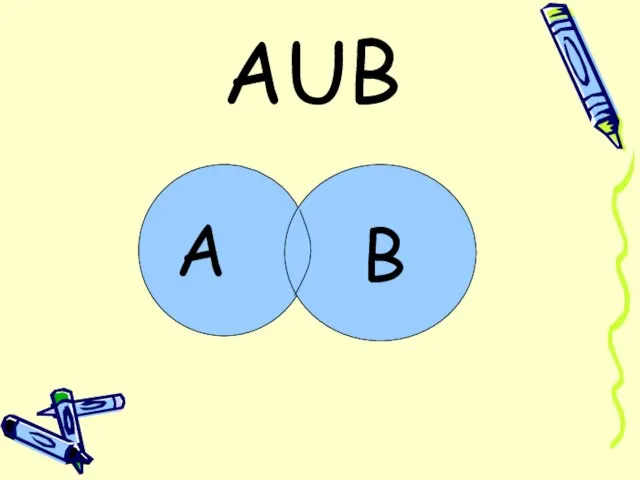
Слайд 10 Наступает либо А, либо В, либо А и В вместе.

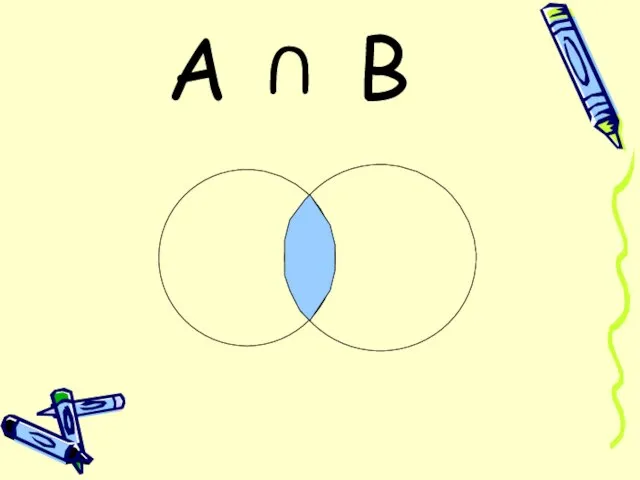
Слайд 13 Наступает если наступают оба события А и В.

Слайд 14Задание №1
Бросают одну игральную кость. Событие А – «выпало четное число

очков». Событие В – «выпало число очков кратное 3». Выпишите все элементарные события, благоприятствующие событию АUВ
Слайд 15Задание №2
Бросают одну игральную кость. Событие А – «выпало четное число очков».

Событие В – «выпало нечетное число очков». Выпишите все элементарные события, благоприятствующие событию АUВ











 НазванияХимическихЭлементов
НазванияХимическихЭлементов Акты применения права. Характеристика и классификация
Акты применения права. Характеристика и классификация САМЫЕ-САМЫЕ
САМЫЕ-САМЫЕ Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году
Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году Невидимые нити (2 класс)
Невидимые нити (2 класс) НИКОЛАЯ ДМИТРИЕВИЧА ПАПАЛЕКСИ
НИКОЛАЯ ДМИТРИЕВИЧА ПАПАЛЕКСИ Реализация принципов нормативно-подушевого финансирования на муниципальном уровне
Реализация принципов нормативно-подушевого финансирования на муниципальном уровне Верейская по деньгам - ИТОГ
Верейская по деньгам - ИТОГ Дизайнер в отечественном ИТ бизнесе: многообразие деятельности, недооцененные компоненты профессионализма, стратегия роста Сер
Дизайнер в отечественном ИТ бизнесе: многообразие деятельности, недооцененные компоненты профессионализма, стратегия роста Сер Симметрия в архитектуре
Симметрия в архитектуре Презентация на тему Основные типы задач на проценты
Презентация на тему Основные типы задач на проценты  Вопросы внедрения национальной Интернет-адресации (IDN) .КАЗ
Вопросы внедрения национальной Интернет-адресации (IDN) .КАЗ Шаблон. Название темы
Шаблон. Название темы Презентация на тему Деревья
Презентация на тему Деревья  Учимся рисовать синичку (1)
Учимся рисовать синичку (1) Ох, уж эта функция
Ох, уж эта функция ЕДИНАЯ СИСТЕМА КЛАССИФИКАТОРОВ АНАЛИТИЧЕСКИХ ДАННЫХ
ЕДИНАЯ СИСТЕМА КЛАССИФИКАТОРОВ АНАЛИТИЧЕСКИХ ДАННЫХ Основы программирования промышленных роботов
Основы программирования промышленных роботов Образ матери в искусстве
Образ матери в искусстве Исследование опорно-двигательного аппарата учащихся Кугультинской средней школы
Исследование опорно-двигательного аппарата учащихся Кугультинской средней школы Шар ( сфера )
Шар ( сфера ) Школа нумерологии Светланы Сорокиной. Основы нумерологии. Базовый курс. Урок 2
Школа нумерологии Светланы Сорокиной. Основы нумерологии. Базовый курс. Урок 2 С Новым годом поздравляю
С Новым годом поздравляю Презентация на тему Книжная миниатюра Востока
Презентация на тему Книжная миниатюра Востока  О ДОЛГОСРОЧНОМ РЕГУЛИРОВАНИИ ТАРИФОВ НА УСЛУГИ ПО ПЕРЕДАЧЕ ТЕПЛОВОЙ ЭНЕРГИИ ООО «СВЕРДЛОВСКАЯ ТЕПЛОСНАБЖАЮЩАЯ КОМПАНИЯ»
О ДОЛГОСРОЧНОМ РЕГУЛИРОВАНИИ ТАРИФОВ НА УСЛУГИ ПО ПЕРЕДАЧЕ ТЕПЛОВОЙ ЭНЕРГИИ ООО «СВЕРДЛОВСКАЯ ТЕПЛОСНАБЖАЮЩАЯ КОМПАНИЯ» Начало Второй Мировой Войны
Начало Второй Мировой Войны Понятие психологии
Понятие психологии Страховые фонды Понятие, сущность, основные формы
Страховые фонды Понятие, сущность, основные формы