Слайд 210110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Актуальность проблемы
Распознавание образов — один из важнейших разделов информатики и кибернетики. Этот

раздел связан с решением широкого круга задач науки и техники на основе общей логической концепции классификации.
Актуальность проблемы распознавания образов постоянно возрастает. Это обусловлено усложнением технологии и организации производства, необходимостью переработки больших потоков информации, расширением круга плохо формализуемых задач принятия решений.
Большие трудности связаны с моделированием нестационарных и плохо определенных процессов, расплывчатых целей, нечетких ограничений.
Слайд 310110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Цель преддипломной практики
Анализ современных методов распознавания образов
Задачи преддипломной практики:
Провести аналитический обзор

научной литературы;
Сравнить методы распознавания;
Выбрать оптимальный метод распознавания образов и решить задачи данным методом;
Слайд 410110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Формулировка задач распознавания образов
Задачи распознавания образов как задачи автоматизации получения и обработки

данных, анализа закономерностей в массивах информации могут быть разбиты на три группы:
выделение, формирование и оценка существенных признаков (факторов), преобразование пространства признаков;
анализ закономерностей размещения элементов конечного множества в многомерном фазовом пространстве;
разбиение пространства на классы эквивалентности, отнесение элементов пространства к классам.
Слайд 510110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Основные определения
Образ - это некоторое структурированное приближенное описание (эскиз) изучаемого объекта, явления

или процесса.
При построении математических моделей распознавания образов под образом мы будем понимать просто некоторое множество объектов, сходных друг с другом в определенном отношении.
Классы - это объединения объектов (явлений), отличающиеся общими свойствами, интересующими человека.
Система распознавания образов – это построение на основе систематических теоретических и экспериментальных исследований эффективных вычислительных средств для отнесения описаний с объектов, явлений, процессов к соответствующим классам.
Слайд 610110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
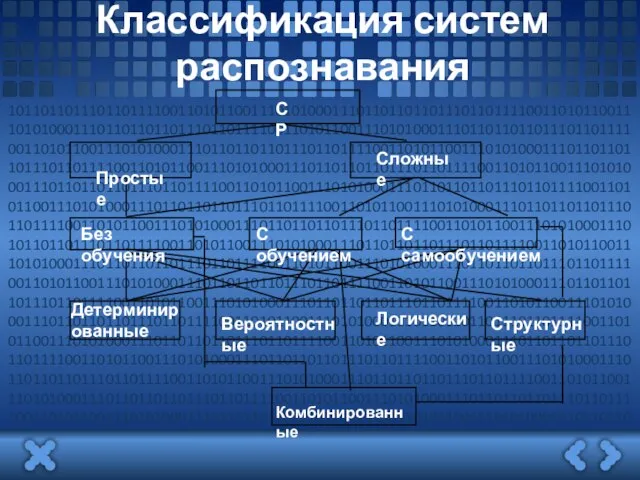
Классификация систем распознавания
Слайд 710110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Пример
Пусть задано множество объектов или явлений W ={w1 , w2 ,....,wl };
Введем

множество из r возможных вариантов разбиения этих объектов W на классы (варианты алфавита классов) A ={A1, A2, ..., Ar}
Таким образом, с учетом возможного отказа от решений в каждом варианте множество объектов W подразделяется на свое число классов:
в варианте A1 - на (m1 +1) классов;
в варианте A2 - на (m2 +1) классов;
...........................................................
в варианте Ar - на (mr +1) классов.
Иными словами здесь мы располагаем r алфавитами классов.
В соответствии с вариантом алфавита классов (As) исходные объекты (явления) разбиваются на ms "решающих" классов
Слайд 810110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Пример
W = {W(1/As ), W(2/As ), W(3/As ),....... , W(ms /As )},

где естественно "1", "2",..... - номера классов; As - вариант алфавита классов, где s=1,2,....,r.
Например: W(1/As ) = {W1 ,W2 ,..Wk }; W(2/As ) = { Wk+1 ,Wk+2 ,..,Wl } и т.д.
Таким образом, мы располагаем подмножествами классифицированных объектов. Если при этом располагаем априорным словарем признаков X = { x1 , x2 , ..., xn },
и притом размеры указанных подмножеств классифицированных объектов таковы, что соответствующие выборки признаков представительны (в каждом классе достаточное в статистическом смысле число объектов),то тогда тем или иным способом может быть проведено описание каждого из классов на языке этого словаря.
Слайд 910110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Пример
В детерминированном случае это достаточно просто. Каждый класс имеет свои эталоны со

своими характеристиками как наборами параметров, представляющих собой признаки распознавания:
Xik [W(j/As )], где i = 1,n - число признаков распознавания;
j = 1,m - число классов; k = 1,Nэj - число эталонов в j-том классе.
При статистическом подходе (вероятностные признаки и вероятностная СР) описание это:
- априорные вероятности классов P[W(i/As )];
- функции условных ПРВ f{X/[W(i/As )]};
Наличие описаний классов уже позволяет определять решающие правила (решающие границы), использование которых обеспечивает минимизацию ошибок при распознавании неизвестных объектов.
Слайд 1010110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Пример
Если бы не было ограничений на величину ресурсов, ассигнуемых на построение СР,

а именно на создание измерительных средств, предназначенных для определения признаков, то можно было бы считать, что как алфавит классов, так и словарь признаков определены и можно приступать к построению системы.
Реально при создании сложных систем не бывает без указанных ограничений. При этом, когда речь идет об ограничениях, это не обязательно финансовые ограничения. Достаточно часто в качестве таковых могут выступать ограничения на быстродействие, память и т.п.
Слайд 1110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Методы распознавания образов
1 Метод МГУА
2 Интенсиональные методы
2.1 Методы основанные на оценках

плотностей распределения значений признаков
2.2 Методы основанные на предложениях о классе решающих функций
3 Логические методы
4 Лингвистические (структурные) методы
5 Экстенсиональные методы
5.1 Метод сравнения с прототипом
5.2 Метод k-ближайших соседей
6 Метод потенциалов
7 Метод проекций
Слайд 1210110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
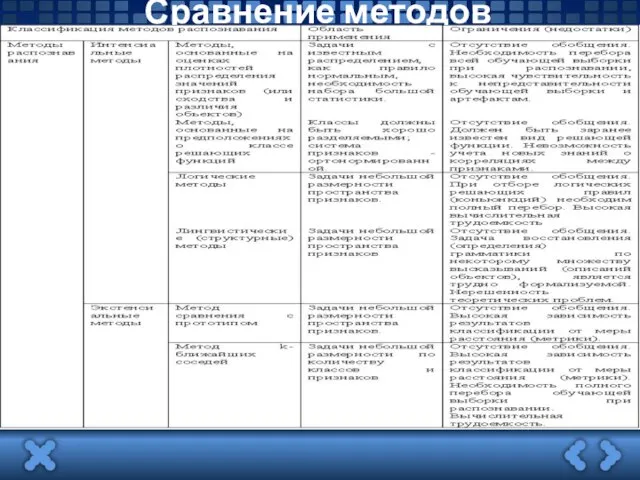
Сравнение методов
Слайд 1310110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Сравнение методов

Слайд 1410110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Метод комитетов
Комитетом системы ограничений называется конечное множество элементов такое, что каждому ограничению

удовлетворяют более половины (простое большинство) элементов этого множества.
Комитетные конструкции позволяют получать практически приемлемые решения и других видов плохо формализуемых задач планирования, управления, прогнозирования и распознавания образов.
Комитетные конструкции как некоторое направление обобщения понятия решения на случае несовместных систем соотношений — один из основных подходов в распознавании образов.
Слайд 1510110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Метод комитетов
Интерес к комитетным конструкциям объясняется как их полезностью в теории принятия

решений, приложениями в несобственных задачах оптимизации, так и следующими важными в решении задач распознавания образов характеристиками:
— комитетная дискриминантная функция, безошибочно разделяющая
объекты материала обучения, строится при весьма слабых и легко контролируемых требованиях к обучающему множеству;
— при построении комитетов можно ограничиться определенным
фиксированным классом функций и на его основе наращивать сложность
решающего правила до той степени, которая отвечает сложности решаемой
задачи классификации.
Слайд 1610110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
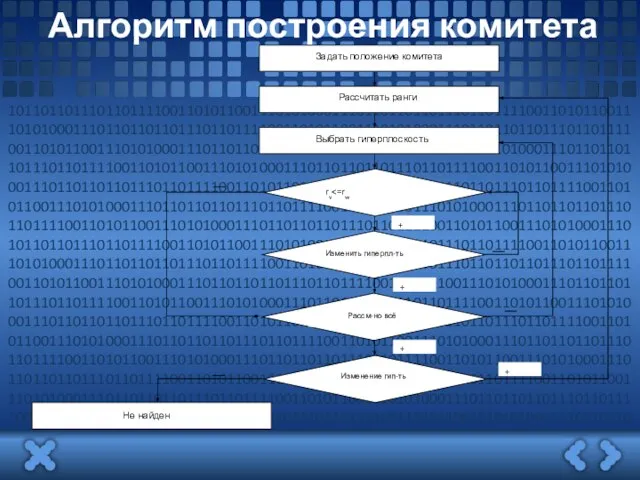
Алгоритм построения комитета
Слайд 1710110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Результаты работы
Мною был проведен аналитический обзор научной литературы, докладов, статей по распознаванию

образов. Выделены основные определения и методы распознавания.
Сформулированы и решены основные задачи распознавания образов.
На основе анализа выявлен оптимальный метод распознавания – Метод комитетов. Выделены основные определения и алгоритм построения комитета.
Слайд 1810110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110
10110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010001110110110
Перспективы
Продолжением работы будет рассмотрение выбранного метода комитетов.
Построение метода, решение задач данным

методом и сравнение с другими методами распознавания.

















 Этапы принятия решения
Этапы принятия решения Викторина Iч 2022 26.10
Викторина Iч 2022 26.10 Режущий инструмент лущильных станков
Режущий инструмент лущильных станков Презентация на тему На пути к индустриальной эре
Презентация на тему На пути к индустриальной эре  Транспортно-пересадочные узлы в рамках реализации комплексного инвестиционного проекта «Реконструкция и развитиеМалого кольца
Транспортно-пересадочные узлы в рамках реализации комплексного инвестиционного проекта «Реконструкция и развитиеМалого кольца Презентация (2)
Презентация (2) Петрович. Моя корзина
Петрович. Моя корзина Бер өн менән генә айырылған һүҙҙәр уйла
Бер өн менән генә айырылған һүҙҙәр уйла Источники и системы теплоснабжения
Источники и системы теплоснабжения Природный стиль. Драма
Природный стиль. Драма Уильям Шекспир
Уильям Шекспир Как усовершенствовать учебную деятельность
Как усовершенствовать учебную деятельность Декларация о правах ребенка
Декларация о правах ребенка Ташкент – столица Узбекистана
Ташкент – столица Узбекистана История становления СПО НИКА УралГУФК
История становления СПО НИКА УралГУФК Месяц безопасности
Месяц безопасности Презентация на тему Родная природа в стихотворениях русских поэтов 19 века
Презентация на тему Родная природа в стихотворениях русских поэтов 19 века Рельеф Южной Америки
Рельеф Южной Америки Yarema Zyelyk
Yarema Zyelyk Еко-туризм в селі Дмитрівка, Одеській області
Еко-туризм в селі Дмитрівка, Одеській області Правила проведения аварийно-спасательных работ при обрушении зданий и сооружений
Правила проведения аварийно-спасательных работ при обрушении зданий и сооружений Карьера
Карьера Акционерный капитал
Акционерный капитал Стилистическая эволюция в творчестве Матиса Готхарта-Нитхарта
Стилистическая эволюция в творчестве Матиса Готхарта-Нитхарта ПРЕДВАРИТЕЛЬНЫЕ ИТОГИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ ОМСКОЙ ОБЛАСТИ В 2010 ГОДУ
ПРЕДВАРИТЕЛЬНЫЕ ИТОГИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ ОМСКОЙ ОБЛАСТИ В 2010 ГОДУ Самообразование педагога
Самообразование педагога Олимпийские игры. Где и когда проходили первые Олимпийские игры
Олимпийские игры. Где и когда проходили первые Олимпийские игры Таёжная область Северного Урала
Таёжная область Северного Урала