Районный конкурс «Юные лидеры образования»

«Три великих задачи древности»

Здравствуйте. Спасибо, что позволили мне поделится с вами своими мыслями. Сегодня я расскажу вам о трёх задачах древности, над которыми ломали головы многие великие люди.
1. Квадратура круга
2. Трисекция угла
3. Удвоение куба
Сразу оговорюсь, что в моей работе нет ни актуальности, ни новизны, ни кокой - либо практической значимости. Ведь задачам этим по четыре тысячи лет.
И так я начну…

"Квадратура круга"

Задача заключается в том, чтобы построить сторону квадрата равновеликому данному кругу.
Для решения этой задачи я воспользовалась свойствами плоской кинематической кривой – эвольвентой.

Эвольвента (развёртка) данной кривой АВ, кривая PQ , описываемая концом М гибкой нерастяжимой нити (закреплённой в некоторой точке), сматываемой с кривой АВ (см. рис.1). Сама кривая АВ называется эволютой.

Есть несколько способов построения этой кривой. Я строила её таким образом. 1. Взяла круг.
2. Намотала на него нить.
3. К свободному концу нити привязала карандаш.
4. Наметила центр круга и совместила его с точкой на листе бумаги.
5. Прижимая круг к бумаге и натягивая карандашом нить, провела кривую (см. рис.2).

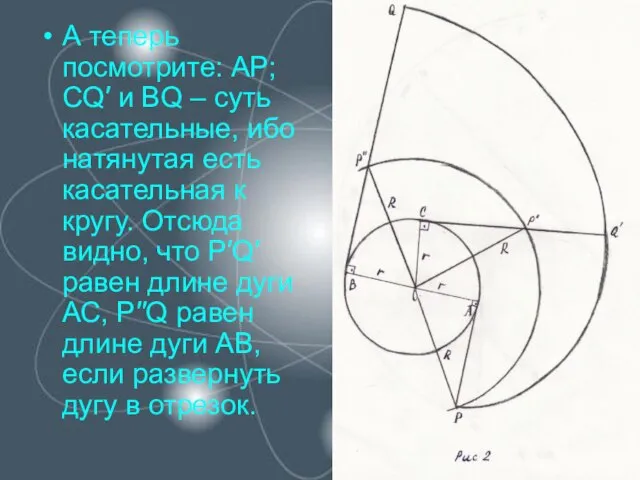
А теперь посмотрите: АР; СQ′ и BQ – суть касательные, ибо натянутая есть касательная к кругу. Отсюда видно, что P′Q′ равен длине дуги АС, P′′Q равен длине дуги АВ, если развернуть дугу в отрезок.

Пусть нам дан круг радиуса r .
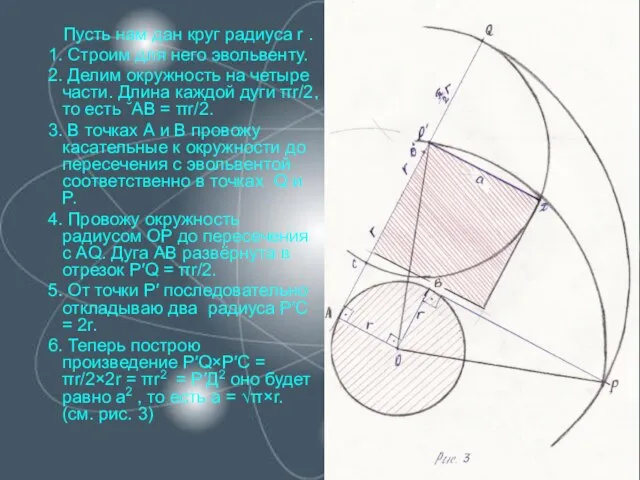
1. Строим для него эвольвенту.
2. Делим окружность на четыре части. Длина каждой дуги πr/2, то есть ˘АВ = πr/2.
3. В точках А и В провожу касательные к окружности до пересечения с эвольвентой соответственно в точках Q и P.
4. Провожу окружность радиусом ОР до пересечения с АQ. Дуга АВ развёрнута в отрезок P′Q = πr/2.
5. От точки P′ последовательно откладываю два радиуса P′C = 2r.
6. Теперь построю произведение P′Q×P′C = πr/2×2r = πr2 = P′Д2 оно будет равно а2 , то есть а = √π×r. (см. рис. 3)

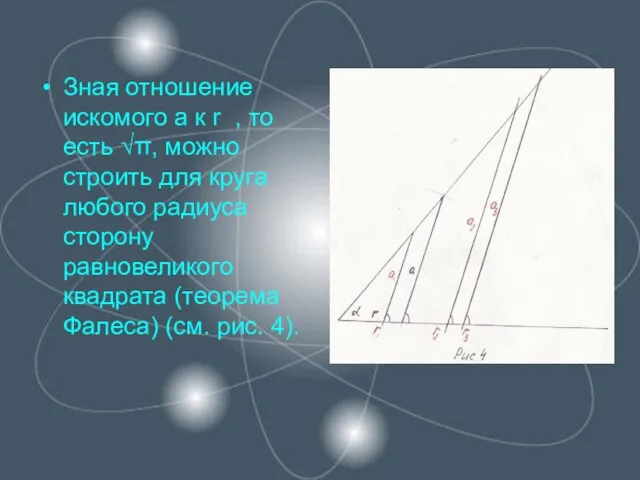
Зная отношение искомого а к r , то есть √π, можно строить для круга любого радиуса сторону равновеликого квадрата (теорема Фалеса) (см. рис. 4).

"Трисекция угла"

Задача заключается в делении угла на три равные части. Для этого я снова использовала эвольвенту.

Пусть дан угол АОВ.(см. рис. 5)
1. Размещаем его в окружности таким образом, чтобы он был центральным (А′О′В′) . Перенести угол не проблема. Эвольвенту можно использовать однажды вычерченную.
2. В точках А′ и В′ проводим касательные А′Д и В′Н до пересечения с эвольвентой.
3. Из точки О′ провожу окружность радиусом О′Н до пересечения с А′Д. Дуга А′В′ развернётся в отрезок СД.
4. Отрезок СД делю на три равные части (можно разделить на n частей). Для этого провожу под углом к СД СЕ и откладываю на нём три равных отрезка (СF′=F′G′=G′E). Точку Е соединяю с точкой Д и параллельно ей провожу G′G и F′F. Отрезок СF является третьей частью отрезка СД.
5. Провожу окружность из О′ радиусом O′F до пересечения с эвольвентой в точке N.
6. Провожу касательную МN к окружности. Для этого О′N делю пополам и как на диаметре строю полуокружность. Точка пересечения окружности и полуокружности даст мне точку касания М. Угол О′МN прямой, так как он опирается на диаметр О′N.
7. Угол МО′В′ - искомый, так как дуга МВ′ = N′N = CF = ⅓ ˘ A′B′.

Таким образом угол можно разделить на n частей. Вы скажете, что я забыла про основное условие задач: построение можно производить только с помощью циркуля, линейки без делений и карандаша. Я реалистка и, если было доказано, что построение при помощи указанных инструментов невозможно, я спорить не буду. Это кумир моих сверстников поёт о том, что «знает то, что невозможное возможно». Меня его откровения не трогают. Не может же человек при нормальных условиях ходить по потолку или, скажем, идти по воде, аки по суху. Но ведь создаются условия, при которых становится возможными подобные действия. Так вот, эвольвента, а точнее диск с нитью, помогли мне сделать невозможное возможным. Многие горячие головы подвинулись рассудком, решая эти задачи, но, с другой стороны, много открытий было совершено при попытках их решения. Одно из них предложенное Диностратом квадратриса. Согласна, с её помощью решаются обе задачи, но сама кривая неестественная и трудноисполнимая. Эвольвента намного проще и её можно начертить по точкам, используя аналитическое уравнение. Но вернёмся к нашим задачам.

"Удвоение куба"

Я решила использовать конические сечения, для этого мне пришлось брать уроки начертательной геометрии.
Известно:
1. Сечение конуса плоскостью перпендикулярной оси симметрии даёт окружность.
2. Сечение конуса плоскостью параллельной образующей даёт параболу.
3. В остальных случаях либо эллипс, либо гипербола.
Пусть дан конус с углом 90º между образующими (см. рис. 6).

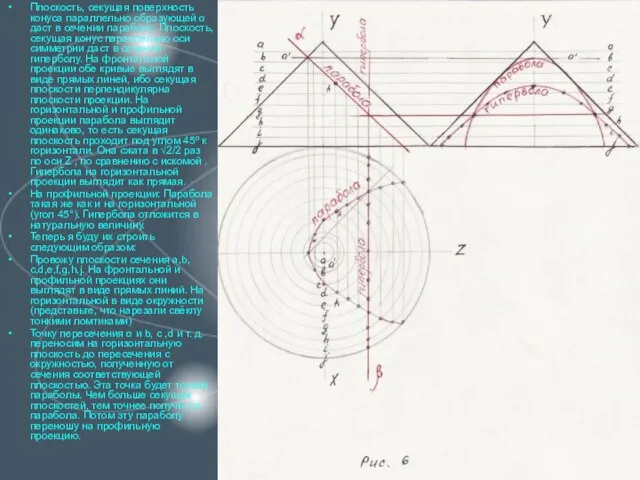
Плоскость, секущая поверхность конуса параллельно образующей α даст в сечении параболу. Плоскость, секущая конус параллельно оси симметрии даст в сечении гиперболу. На фронтальной проекции обе кривые выглядят в виде прямых линей, ибо секущая плоскости перпендикулярна плоскости проекции. На горизонтальной и профильной проекции парабола выглядит одинаково, то есть секущая плоскость проходит под углом 45º к горизонтали. Она сжата в √2/2 раз по оси Z , по сравнению с искомой . Гипербола на горизонтальной проекции выглядит как прямая.
На профильной проекции: Парабола такая же как и на горизонтальной(угол 45°). Гипербола отложится в натуральную величину.
Теперь я буду их строить следующим образом:
Провожу плоскости сечения a,b,с,d,e,f,g,h,j. На фронтальной и профильной проекциях они выглядят в виде прямых линий. На горизонтальной в виде окружности(представьте, что нарезали свёклу тонкими ломтиками)
Точку пересечения α и b, c ,d и т. д. переносим на горизонтальную плоскость до пересечения с окружностью, полученную от сечения соответствующей плоскостью. Эта точка будет точкой параболы. Чем больше секущих плоскостей, тем точнее получится парабола. Потом эту параболу переношу на профильную проекцию.

Итак, я с достаточной точностью, с помощью циркуля и линейки могу построить и параболу и гиперболу, следовательно я могу графически решить x2 = 1/x → x 3 = 1 и x2 = 2/x → x 3 = 2, то есть извлечь кубический корень из двух, а это и есть ключ к решению задачи. Однако, и параболу и гиперболу надо строить в единой системе координат, для этого надо одну из них повернуть на 45°, ибо в данной системе гипербола имеет совсем другое аналитическое выражение (см рис. 7).