Слайд 2 Три пути ведут к знанию:
путь размышления – это путь
самый
благородный, путь
подражания – это путь самый
легкий и путь опыта – это
путь самый горький.
Конфуций
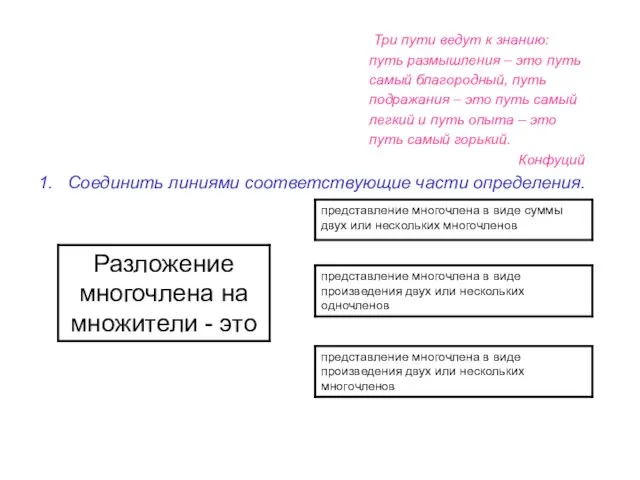
1. Соединить линиями соответствующие части определения.
Слайд 3 Три пути ведут к знанию:
путь размышления – это путь
самый
благородный, путь
подражания – это путь самый
легкий и путь опыта – это
путь самый горький.
Конфуций
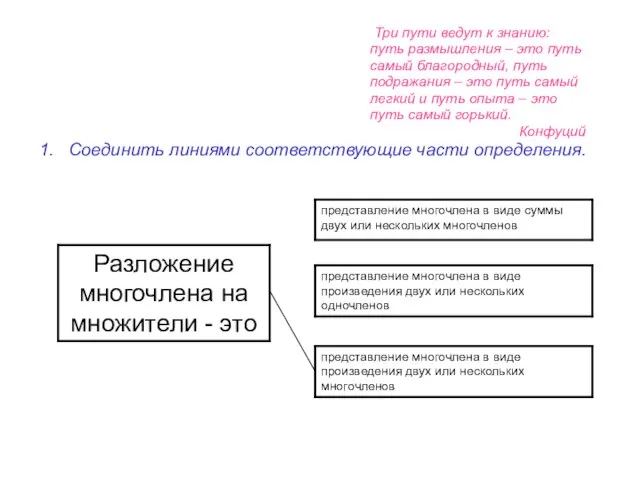
1. Соединить линиями соответствующие части определения.
Слайд 42. Завершить утверждение.
Представление многочлена в виде произведения одночлена и многочлена называется

Слайд 52. Завершить утверждение.
Представление многочлена в виде произведения одночлена и многочлена называется вынесением

общего множителя за скобки.
Слайд 63. Восстановить порядок выполнения действий при разложении многочлена на множители способом группировки.
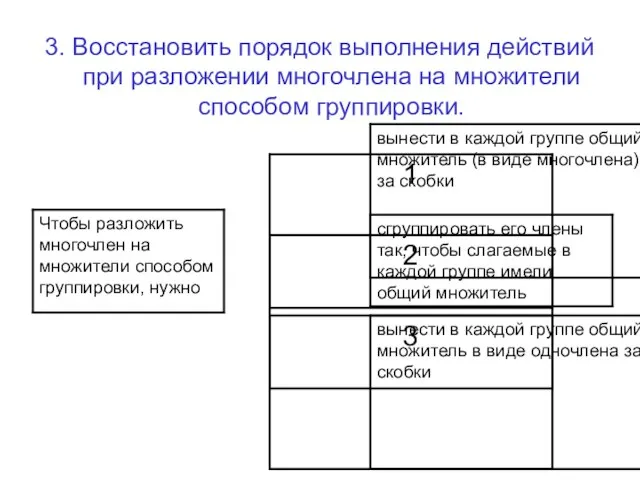
Слайд 73. Восстановить порядок выполнения действий при разложении многочлена на множители способом группировки.
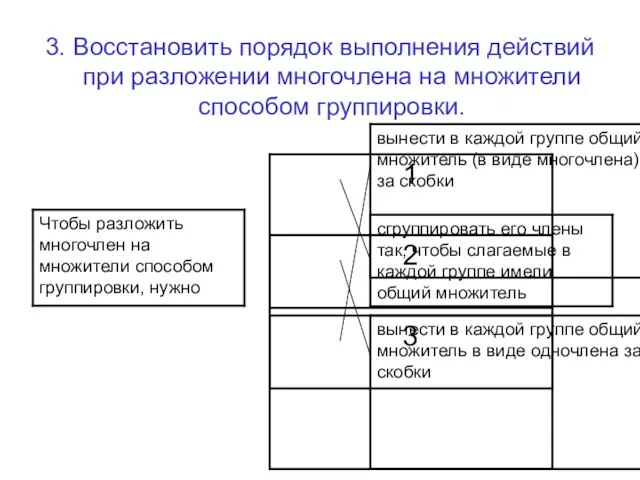
Слайд 84. Отметить знаком «+» верные выражения.

Слайд 94. Отметить знаком «+» верные выражения.

Слайд 10Работа по вариантам
Задание. Провести классификацию данных многочленов по способу разложения на множители:
вынесение

общего множителя за скобки;
формула сокращенного умножения;
не раскладывается на множители;
способ группировки.
1 вариант 2 вариант
Слайд 12Задание. Разложите многочлен на множители и укажите, какие приемы использовались при этом.
1)
2)
3)

Слайд 13Решение:
1)
Комбинировали два приема:
вынесение общего множителя за скобки;
использование формул сокращенного умножения.
2)
Комбинировали два приема:
группировку;
использование

формул сокращенного умножения.
3)
Комбинировали три приема:
группировку;
формулы сокращенного умножения;
вынесение общего множителя за скобки.
Слайд 14Прием предварительного преобразования.
Некоторый член многочлена раскладывается на необходимые слагаемые или дополняется путем

прибавления к нему некоторого слагаемого. В последнем случае, чтобы многочлен не изменился, от него отнимается такое же слагаемое.
Слайд 15Разложение на множители
Решение:
Комбинировали три приема:
вынесение общего множителя за скобки;
предварительное преобразование;
группировку.

Слайд 16 Решить уравнение:
Вывод: при разложении многочлена на
множители мы «увидели» полный квадрат
и

таким образом применили еще один прием разложения на
множители: метод выделения полного квадрата.
Слайд 17Самостоятельная работа.
Вариант 1 Вариант 2
Разложить на множители,
используя различные способы.

Слайд 18Ответы к самостоятельной работе:
Вариант 1 Вариант 2


















 Инвестиции в номерной фонд апарт-отеля
Инвестиции в номерной фонд апарт-отеля Викторина по истории изобразительного искусства Древняя Русь
Викторина по истории изобразительного искусства Древняя Русь Оценка пространственных внешних эффектов для России
Оценка пространственных внешних эффектов для России В.Терешкова – первая женщина-космонавт
В.Терешкова – первая женщина-космонавт Я – ребёнок, я - человек!
Я – ребёнок, я - человек! Зоя Космодемьянская
Зоя Космодемьянская История психологии
История психологии Грабли Как мы наступали на грабли…
Грабли Как мы наступали на грабли… Интеллектуада ВУЗОВ Санкт-Петербурга
Интеллектуада ВУЗОВ Санкт-Петербурга Заводські дефекти лакофарбного покриття(ЛФП) тепловозів серії ТЕ33АС
Заводські дефекти лакофарбного покриття(ЛФП) тепловозів серії ТЕ33АС Внешнеполитические интересы
Внешнеполитические интересы Вазоренальная артериальная гипертензия
Вазоренальная артериальная гипертензия И
И Новогодняя вечерника в Хокку
Новогодняя вечерника в Хокку Презентация на тему Что такое функция (7 класс)
Презентация на тему Что такое функция (7 класс) У каждого из нас в жизни случаются трудности
У каждого из нас в жизни случаются трудности Государство и налоги
Государство и налоги Химия - страна чудес
Химия - страна чудес х
х Lifestyle of students in St. Petersburg
Lifestyle of students in St. Petersburg Информация по реализации 83-ФЗ
Информация по реализации 83-ФЗ Олимпийская гордость Санкт-Петербурга. Лондон 2012
Олимпийская гордость Санкт-Петербурга. Лондон 2012 Преобразование рациональных выражений.
Преобразование рациональных выражений. ФИРМА RESPECT Представляет проект: «Деловой школьник!»
ФИРМА RESPECT Представляет проект: «Деловой школьник!» АО Транснефть-Сибирь. Оптимизация передачи документов через КИС ЭХД
АО Транснефть-Сибирь. Оптимизация передачи документов через КИС ЭХД Административно-территориальное деление РФ (1)
Административно-территориальное деление РФ (1) Периметр Площадь
Периметр Площадь Банковский депозит
Банковский депозит