развертки координат

Основные положения
Развертыванием называется такое преобразование, при котором все точки поверхности совмещаются с плоскостью.
Развертка - плоская фигура, получаемая в результате данного преобразования.
Поверхности делятся на развертываемые и неразвертываемые.
Развертываемые совмещаются с плоскостью без разрывов и складок
Для неразвертываемых строятся условные развертки

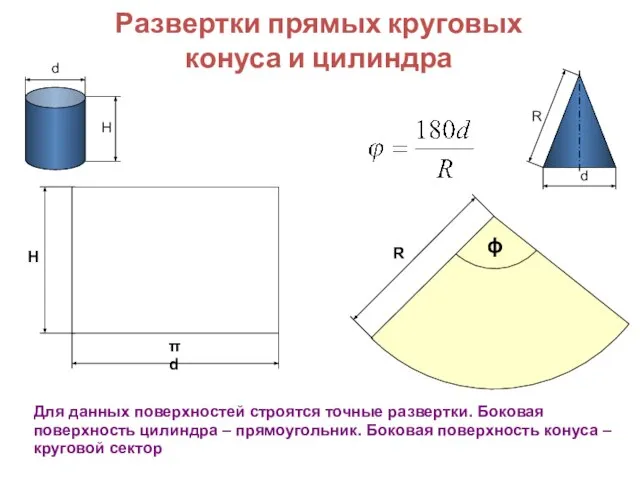
Развертки прямых круговых
конуса и цилиндра
Н
d
Н
d
Для данных поверхностей строятся точные развертки. Боковая поверхность цилиндра – прямоугольник. Боковая поверхность конуса – круговой сектор


Способ нормального сечения
Определяются натуральные величины образующих, если они заданы в общем положении.
Строится нормальное сечение (там, где образующие имеют истинную величину)
Определяется натуральная величина нормального сечения
Строится развертка: периметр нормального сечение «развертывается» в прямую; через его вершины перпендикулярно линии проводятся образующие
Применяется для призматических и цилиндрических поверхностей. Нормальное сечение перпендикулярно образующим и определяет расстояние между ними

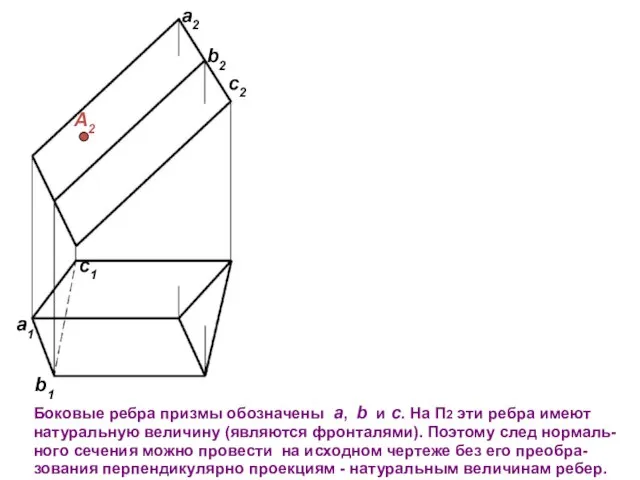
a2
b2
c2
А2
Боковые ребра призмы обозначены a, b и c. На П2 эти ребра имеют натуральную величину (являются фронталями). Поэтому след нормаль-ного сечения можно провести на исходном чертеже без его преобра-зования перпендикулярно проекциям - натуральным величинам ребер.
c1
b1
a1

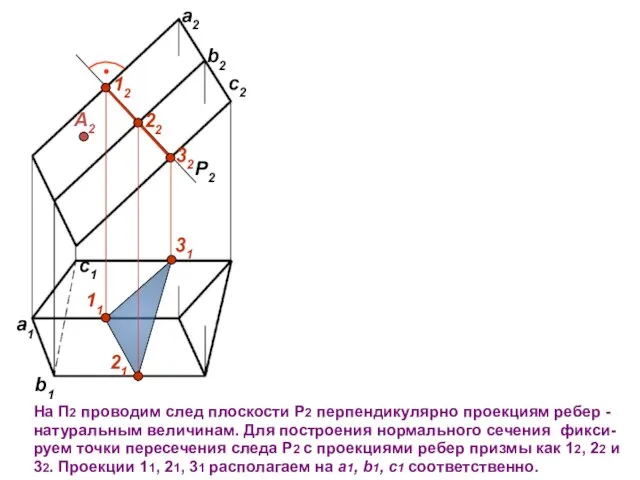
А2
На П2 проводим след плоскости Р2 перпендикулярно проекциям ребер - натуральным величинам. Для построения нормального сечения фикси- руем точки пересечения следа Р2 с проекциями ребер призмы как 12, 22 и 32. Проекции 11, 21, 31 располагаем на a1, b1, c1 соответственно.
b1
a1
c1

P2
12
22
32
А2
Для построения развертки призмы необходима натуральная величина нормального сечения, которой нет на исходном чертеже. Применив способ плоско-параллельного перемещения, найдем проекцию треугольника - натуральную величину 112131.
c1
b1
a1

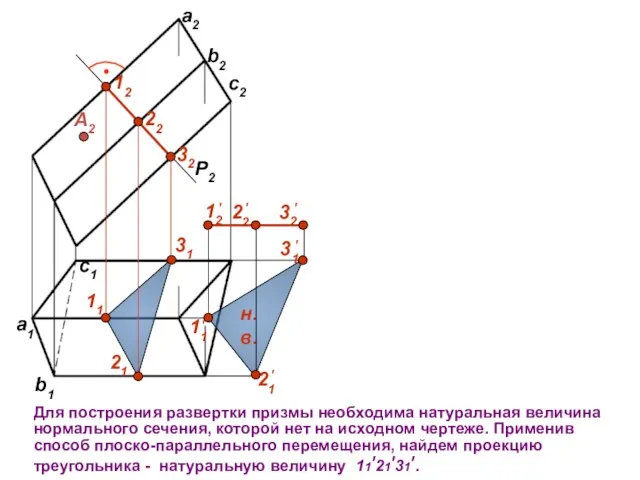
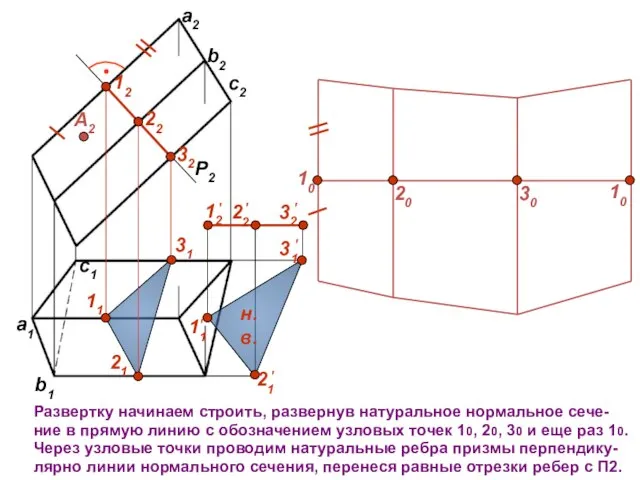
c1
b1
a1
P2
12
22
32
11
31
21
А2
Развертку начинаем строить, развернув натуральное нормальное сече- ние в прямую линию с обозначением узловых точек 10, 20, 30 и еще раз 10. Через узловые точки проводим натуральные ребра призмы перпендику- лярно линии нормального сечения, перенеся равные отрезки ребер с П2.
н.в.

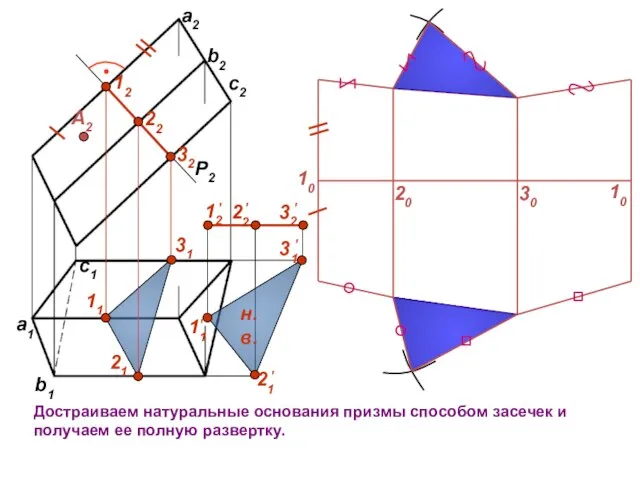
c1
b1
a1
P2
12
22
32
11
31
21
А2
Достраиваем натуральные основания призмы способом засечек и получаем ее полную развертку.
н.в.