Содержание
- 2. Цель: Задачи: изучить и применить бином Ньютона и полиномиальную формулу к решению некоторых комбинаторных задач 1)
- 3. Язык перечислительной комбинаторики
- 4. Бином Ньютона и его свойства 1.Число всех членов разложения на единицу больше показателя степени бинома, т.е.
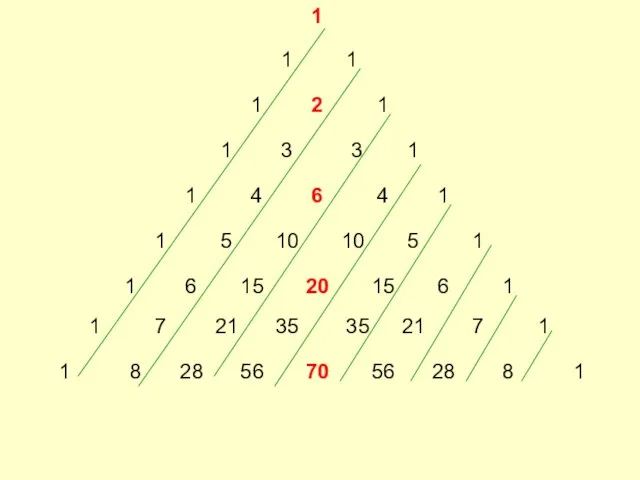
- 5. Треугольник Паскаля ……………………………………………………..
- 6. 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
- 7. Некоторые соотношения для биномиальных коэффициентов Полиномиальная формула
- 8. Задача № 1 Доказать, что делится нацело на 64 при любом натуральном n. Доказательство. Обозначив выражение
- 9. Доказать неравенство Бернулли Задача № 2 c > 1 + n (c – 1), где с
- 10. Задача № 3 Найти разложение степени бинома Решение. Задача № 4 Найти разложение степени тринома
- 12. Скачать презентацию








 Рыба и рыбные продукты
Рыба и рыбные продукты NEFCO Целевые экологические программы
NEFCO Целевые экологические программы Основы законодательства РФ об охране здоровья гражданина
Основы законодательства РФ об охране здоровья гражданина 3.Essen und trinken
3.Essen und trinken Оценка эффективности проекта
Оценка эффективности проекта Анализ материалов
Анализ материалов Отчет по рекламе для студии воздушного фитнеса и йоги Притяжение за март 2019
Отчет по рекламе для студии воздушного фитнеса и йоги Притяжение за март 2019 Cистемная сорганизация бизнес-процессов
Cистемная сорганизация бизнес-процессов муниципальное бюджетное общеобразовательное учреждение "Начальная общеобразовательная школа № 41"
муниципальное бюджетное общеобразовательное учреждение "Начальная общеобразовательная школа № 41" Проектное бюро 3D плюс. Строительство зданий на основе визуализации в 3D формате объемнопланировочных решений
Проектное бюро 3D плюс. Строительство зданий на основе визуализации в 3D формате объемнопланировочных решений Внутреннее и внешнее устройство храма и правила поведения в храме
Внутреннее и внешнее устройство храма и правила поведения в храме Электроустановочные устройства квартиной электросети
Электроустановочные устройства квартиной электросети Рассказ А.И.Солженицына «Один день из жизни Ивана Денисовича»
Рассказ А.И.Солженицына «Один день из жизни Ивана Денисовича» Коза-заяц
Коза-заяц Виды кормов Ландор для кошек
Виды кормов Ландор для кошек Новая линейка мелкой бытовой техники Анна Фендрих Октябрь, 2 2009
Новая линейка мелкой бытовой техники Анна Фендрих Октябрь, 2 2009 Опорные схемы учебно – воспитательного курса «Основы религиозных культур и светской этики».
Опорные схемы учебно – воспитательного курса «Основы религиозных культур и светской этики».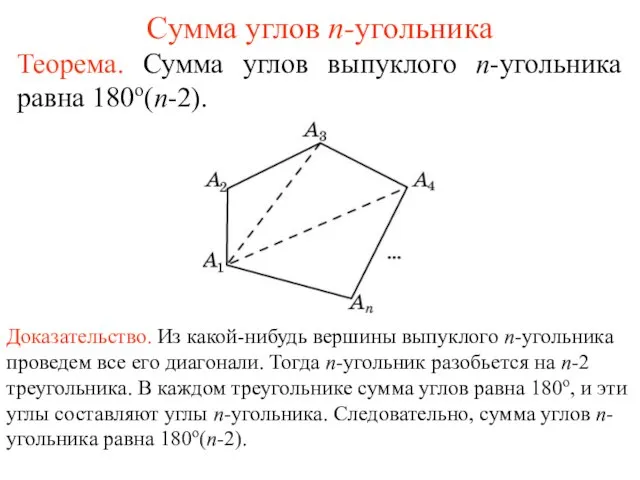 Сумма углов n-угольника
Сумма углов n-угольника Презентация группы компаний «НД»: «Автоматический платежный терминал для АЗС» «Холодная» АЗС в украинских реалиях: законодатель
Презентация группы компаний «НД»: «Автоматический платежный терминал для АЗС» «Холодная» АЗС в украинских реалиях: законодатель Ручная художественная вышивка
Ручная художественная вышивка УП «РЕКЛАМНАЯ КУХНЯ»
УП «РЕКЛАМНАЯ КУХНЯ» Презентация на тему Восклицательные предложения
Презентация на тему Восклицательные предложения Храмы России
Храмы России Картина изохром
Картина изохром Самый лучший спортсмен. Федор Чудинов
Самый лучший спортсмен. Федор Чудинов Игры к празднику Масленицы
Игры к празднику Масленицы Упражнения для мозга
Упражнения для мозга Последний император Николай II
Последний император Николай II