Содержание
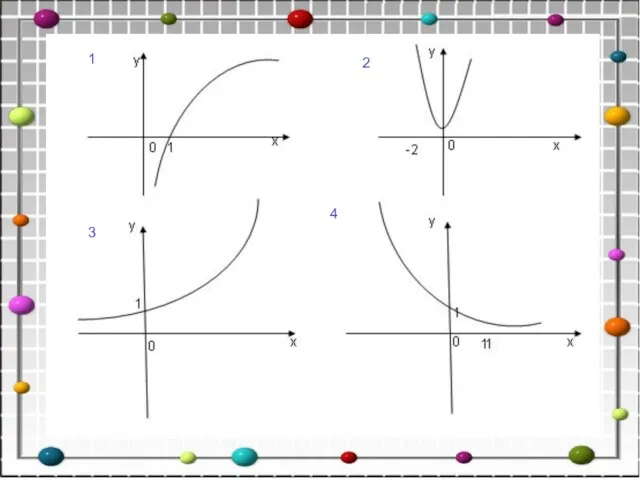
- 2. 1 1 2 3 4
- 3. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ Уравнения вида af(x)=ag(x),где a - положительное число , отличное от 1,и уравнения , сводящиеся
- 4. 1. Решаемые переходом к одному основанию. 2. Решаемые переходом к одному показателю степени. 3. Решаемые вынесением
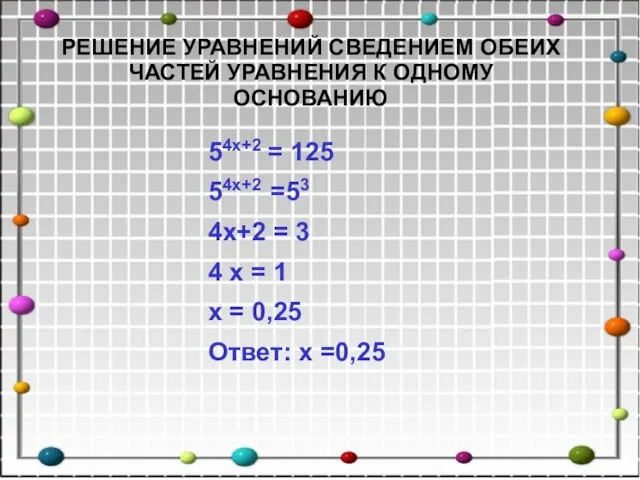
- 5. 54x+2 = 125 54x+2 =53 4x+2 = 3 4 x = 1 x = 0,25 Ответ:
- 6. Решение путем деления Если обе части уравнения степени с равными показателями , то уравнение решают делением
- 7. 3х=2х разделим обе части на 2х 3х: 2х=2х: 2х (1,5)х=1 (1,5)х=(1,5)0 х =0 Пример показательного уравнения,
- 8. Решение разложением на множители Если одна из частей уравнения содержит алгебраическую сумму с одинаковыми основаниями ,
- 9. Пример показательного уравнения, одна из частей которого содержит алгебраическую сумму 3х+1-2*3х-2=25 3х-2*(3х+1-(х-2)-2)=25 3х-2*(33-2)=25 3х-2*25=25 3х-2=1 3х-2=30
- 10. Сведение показательных уравнений к квадратным Одним из наиболее распространенных методов решения уравнений (в том числе и
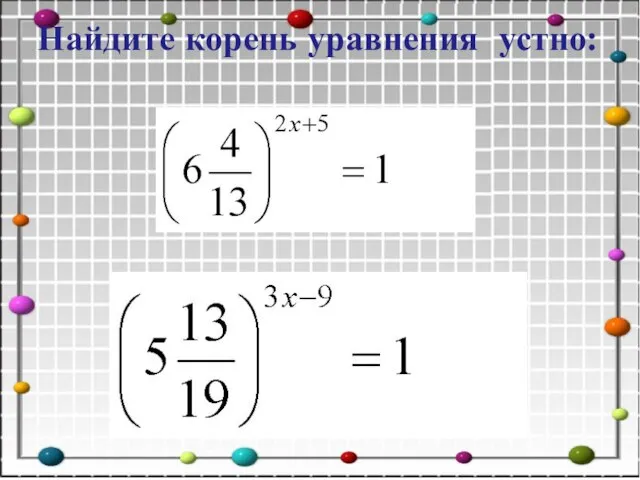
- 11. Найдите корень уравнения устно:
- 12. Найдите корень уравнения устно:
- 14. Скачать презентацию






 Почтовая открытка 23 февраля
Почтовая открытка 23 февраля Изомерия. Классификация органических веществ.
Изомерия. Классификация органических веществ. Обыкновенные дроби (5 класс)
Обыкновенные дроби (5 класс) Проектно- исследовательская деятельность младших школьников
Проектно- исследовательская деятельность младших школьников Стили речи. Введение в стилистику
Стили речи. Введение в стилистику Конкурс как способ организации досугового мероприятия
Конкурс как способ организации досугового мероприятия 1. Oppitunti (2)
1. Oppitunti (2) Разработка рекламных мероприятий по продвижению компании «Горячие туры» в социальных сетях Дипломный проект Рябиги О.С Группа Р
Разработка рекламных мероприятий по продвижению компании «Горячие туры» в социальных сетях Дипломный проект Рябиги О.С Группа Р 20141105_voronezh_segodnya
20141105_voronezh_segodnya Экосистема. Структура экосистемы
Экосистема. Структура экосистемы Славяне в древности
Славяне в древности 29.11.2011г.Студенты группы Ф -22 совместно с кураторомпосетили
29.11.2011г.Студенты группы Ф -22 совместно с кураторомпосетили Презентация 3
Презентация 3 9 «В» Февраль 2012
9 «В» Февраль 2012 дата проведения: 11.01.10Провела:Учитель информатики и ВТХрусцелевская Н.В.Прослушал:5 класс
дата проведения: 11.01.10Провела:Учитель информатики и ВТХрусцелевская Н.В.Прослушал:5 класс Тема: «Великий художник природы – вода».
Тема: «Великий художник природы – вода». Vox – Технология будущего
Vox – Технология будущего Architecture Styles in America
Architecture Styles in America  План проведения педагогического совета 1. Вступление. Анализ выполнения решений предыдущего педагогического совета. 2. Доклад «Сти
План проведения педагогического совета 1. Вступление. Анализ выполнения решений предыдущего педагогического совета. 2. Доклад «Сти Загадочная смерть Маяковского
Загадочная смерть Маяковского Учебное исследование и проектная работа. Основные понятия
Учебное исследование и проектная работа. Основные понятия ЯПОНИЯ
ЯПОНИЯ Характеристика и особенности оформления справок, докладных и объяснительных записок
Характеристика и особенности оформления справок, докладных и объяснительных записок Религиозная толерантность
Религиозная толерантность Презентация на тему Динамика материальной точки. Работа и энергия
Презентация на тему Динамика материальной точки. Работа и энергия
 IT Construct ООО «Ай Ти Констракт»
IT Construct ООО «Ай Ти Констракт» РАЗРАБОТКА И ВНЕДРЕНИЕ УЧЕБНИКОВ ПО БАЙКАЛОВЕДЕНИЮ В ШКОЛЬНОЕ ОБРАЗОВАНИЕ БАЙКАЛЬСКОГО РЕГИОНА
РАЗРАБОТКА И ВНЕДРЕНИЕ УЧЕБНИКОВ ПО БАЙКАЛОВЕДЕНИЮ В ШКОЛЬНОЕ ОБРАЗОВАНИЕ БАЙКАЛЬСКОГО РЕГИОНА Верховный суд США
Верховный суд США