Содержание
- 2. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 3. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 4. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 5. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 6. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 7. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 8. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 9. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 10. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 11. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 12. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 13. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 14. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 15. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 16. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 17. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 18. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 19. 2.1 Решение полиномов Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k =1…n расположены в
- 21. Скачать презентацию
Слайд 22.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
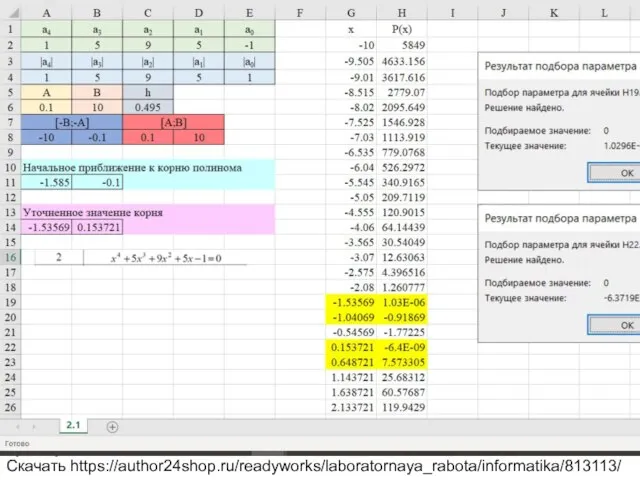
Вариант 2 Уравнение x^4+5x^3+9x^2+5x-1=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813113/
Слайд 32.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
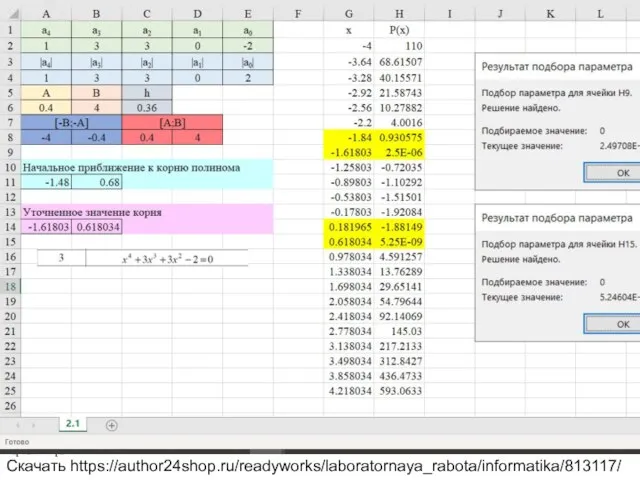
Вариант 3 Уравнение x^4+3x^3+3x^2-2=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813117/
Слайд 42.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
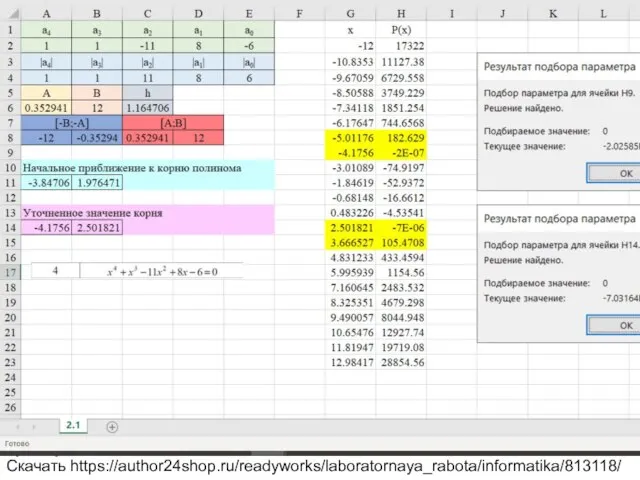
Вариант 4 Уравнение x^4+x^3-11x^2+8x-6=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813118/
Слайд 52.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
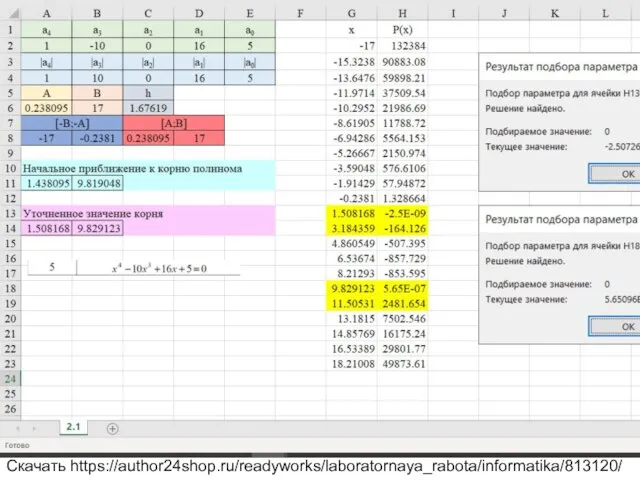
Вариант 5 Уравнение x^4-10x^3+16x+5=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813120/
Слайд 62.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
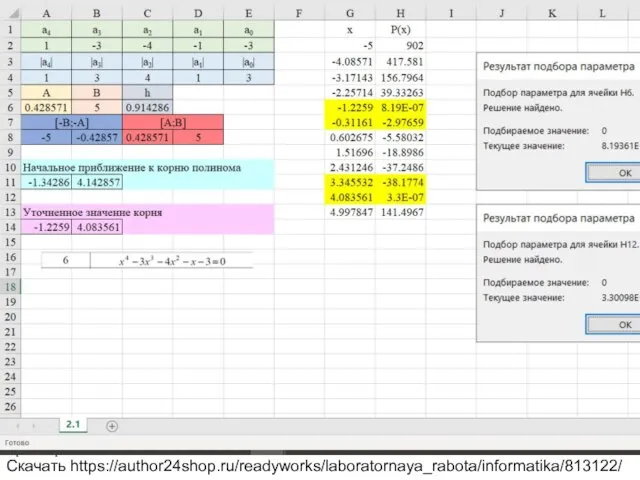
Вариант 6 Уравнение x^4-3x^3-4x^2-x-3=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813122/
Слайд 72.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
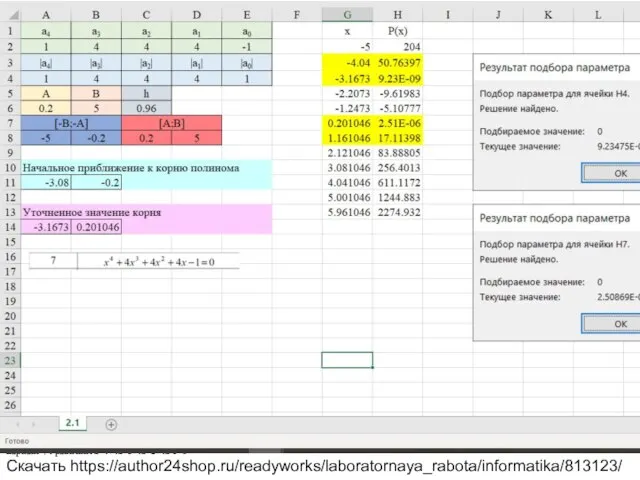
Вариант 7 Уравнение x^4+4x^3+4x^2+4x-1=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813123/
Слайд 82.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
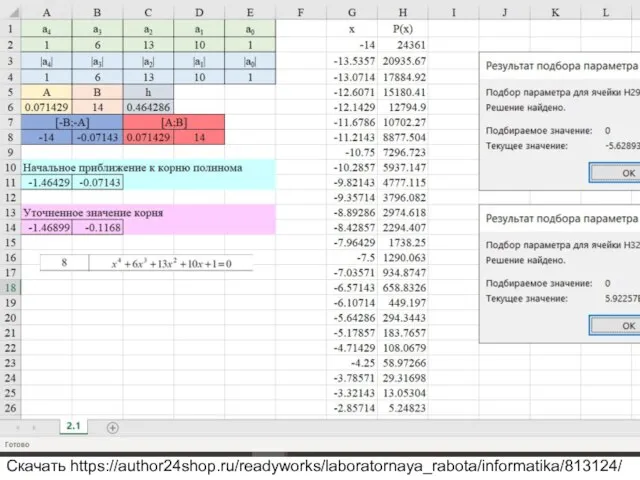
Вариант 8 Уравнение x^4+6x^3+13x^2+10x+1=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813124/
Слайд 92.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
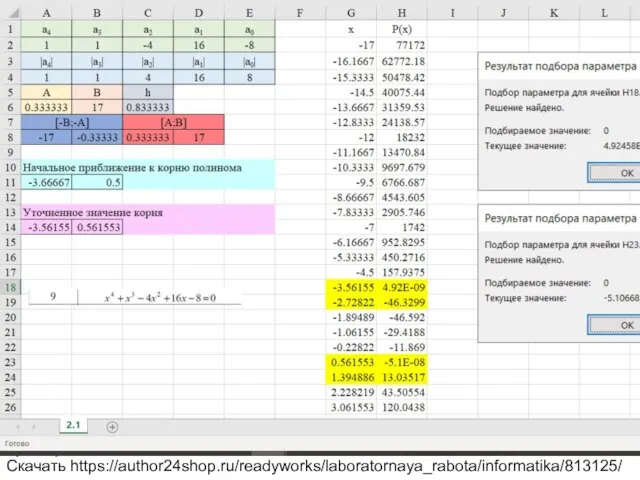
Вариант 9 Уравнение x^4+x^3-4x^2+16x-8=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813125/
Слайд 102.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
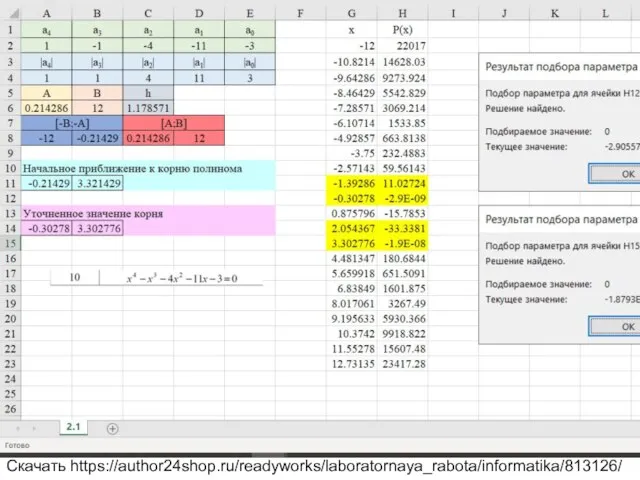
Вариант 10 Уравнение x^4-x^3-4x^2-11x-3=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813126/
Слайд 112.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
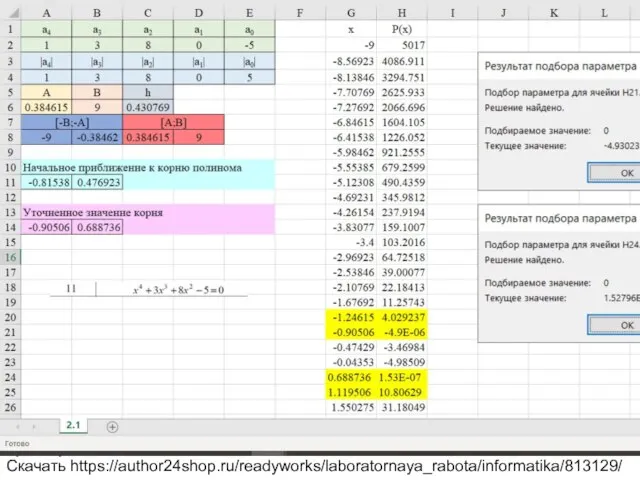
Вариант 11 Уравнение x^4+3x^3+8x^2-5=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813129/
Слайд 122.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
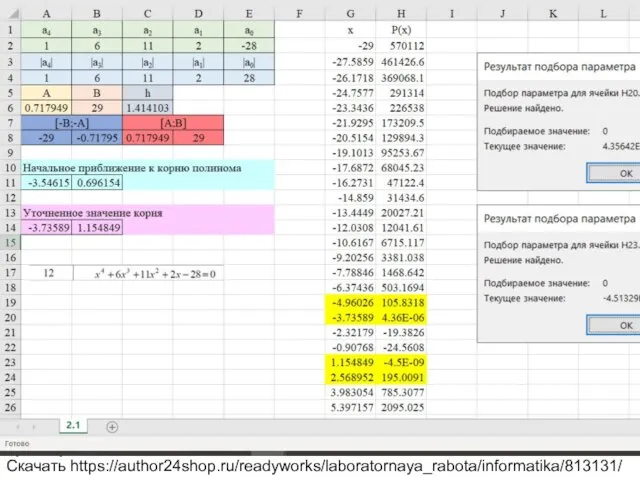
Вариант 12 Уравнение x^4+6x^3+11x^2+2x-28=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813131/
Слайд 132.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
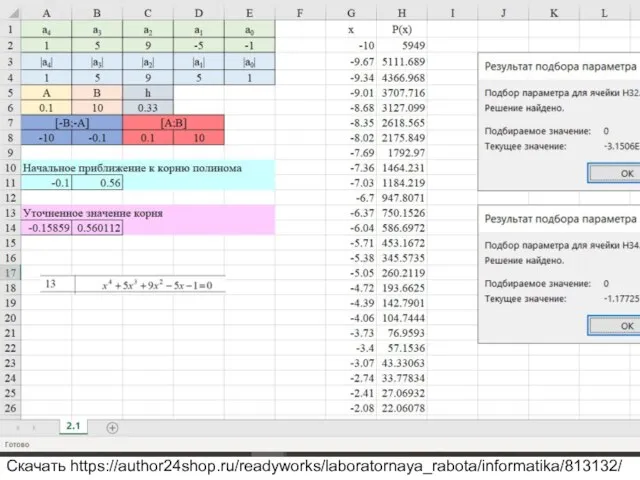
Вариант 13 Уравнение x^4+5x^3+9x^2-5x-1=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813132/
Слайд 142.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
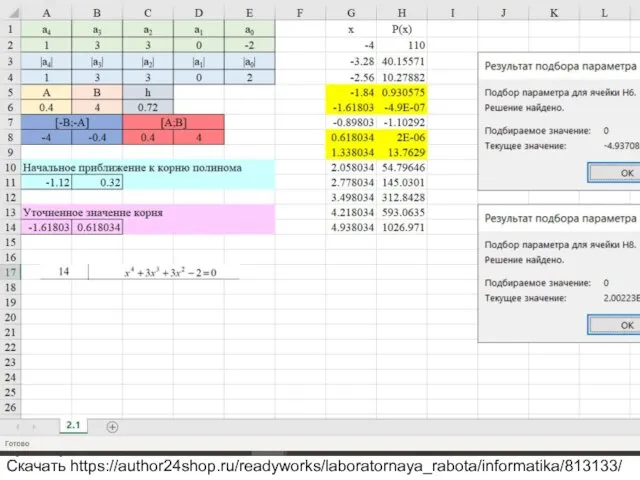
Вариант 14 Уравнение x^4+3x^3+3x^2-2=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813133/
Слайд 152.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
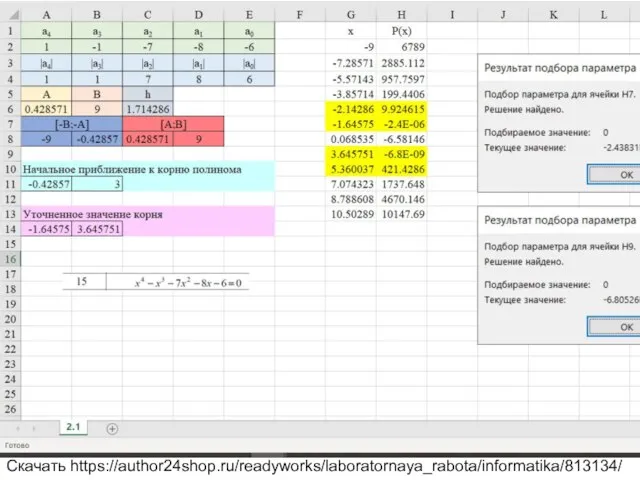
Вариант 15 Уравнение x^4-x^3-7x^2-8x-6=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813134/
Слайд 162.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
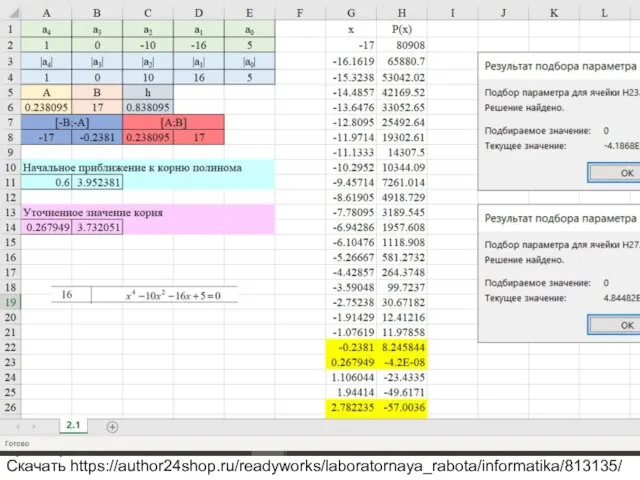
Вариант 16 Уравнение x^4-10x^2-16x+5=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813135/
Слайд 172.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
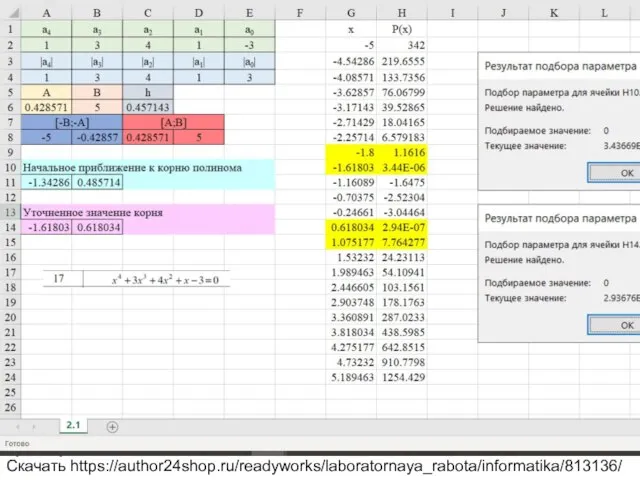
Вариант 17 Уравнение x^4+3x^3+4x^2+x-3=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813136/
Слайд 182.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
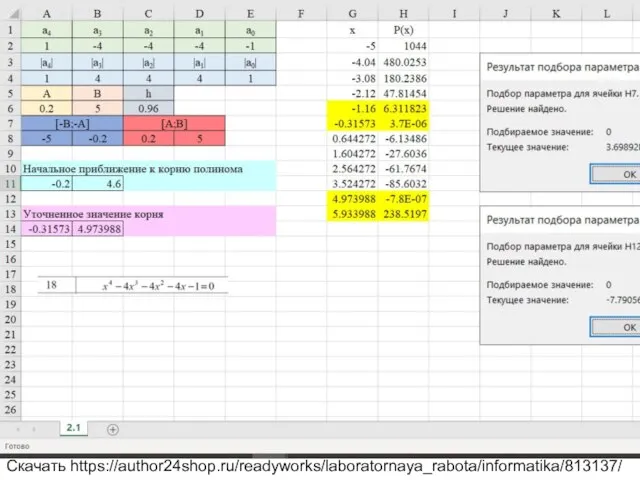
Вариант 18 Уравнение x^4-4x^3-4x^2-4x-1=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813137/
Слайд 192.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
2.1 Решение полиномов
Для полиномов Pn(x)=an^n+an-1x^n-1+…+a1x+a0 модули всех действительных корней xk , k
B=1+max{|an-1|,|an-2|,…,|a0|}/|an|
Следовательно, все действительные положительные корни лежат в интервале [A, B], а все действительные отрицательные корни — в интервале [-B, -A].
Задание 2.1. Корни полинома Найти корни полинома с заданной точностью ε.
Предлагается следующий алгоритм.
1. В диалоговом окне Параметры Excel задать относительную погрешность вычислений корней ε = 0,00001: Файл | Параметры | Формулы | Относительная погрешность.
2. Определить A и B по формуле (2.1), разместив предварительно на листе Excel таблицу коэффициентов выбранного полинома (табл. 2.1).
3. Составить таблицу {x,P(x)}, табулируя полином в найденных интервалах, например с шагом h = (B-A)/10 (см. п. 1.7.2 лабораторной работы 1).
4. Определить две соседние ячейки столбца x , где функция меняет свой знак, и выделить их цветом. Одно из значений, для которого значение функции ближе к нулю, принять за начальное приближение к корню полинома.
5. Уточнить значение корня с помощью сервисной команды Подбор параметра (Данные | Анализ «что если» | Подбор параметра) (рис. 2.1). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома, соответствующее выбранному начальному приближению. В поле Значение ввести 0 (т. е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, где находится начальное приближение к корню полинома.
Рис. 2.1 — Диалоговое окно Подбор параметра
Примечание. В этой ячейке (D3 на рис. 2.1) должно содержаться числовое значение, а не формула, его вычисляющая. Для того чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 2.2). В появившемся диалоговом окне отметить Вставить значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.
Рис. 2.2 — Специальная вставка 44
6. После подбора параметра (нажать ОК) получит значение корня с заданной ранее степенью точности. Процесс повторяется для всех найденных начальных приближений в диапазонах, определяемых формулой (2.1).
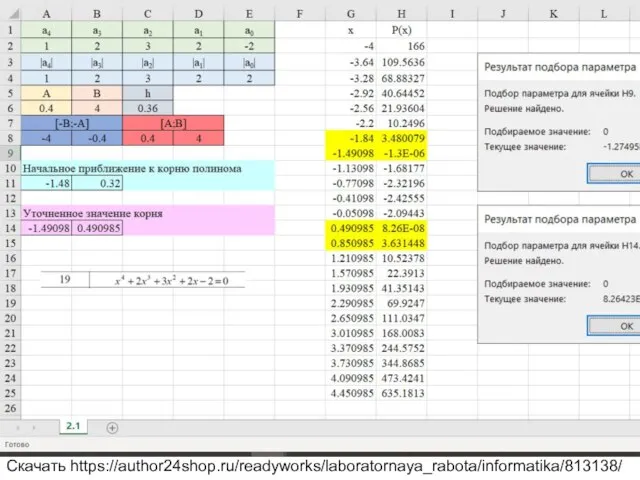
Вариант 19 Уравнение x^4+2x^3+3x^2+2x-2=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813138/
 Структурно-функциональные особенности мозгового кровообращения
Структурно-функциональные особенности мозгового кровообращения ОпытПроекты выполнялись для следующих Заказчиков(часть на субподряде у системных интеграторов)
ОпытПроекты выполнялись для следующих Заказчиков(часть на субподряде у системных интеграторов) История космических побед
История космических побед Таблица единиц времени
Таблица единиц времени ИНДЕКС ПОТРЕБИТЕЛЬСКИХ ЦЕН теория и практика
ИНДЕКС ПОТРЕБИТЕЛЬСКИХ ЦЕН теория и практика Презентация на тему Викторина по ПДД
Презентация на тему Викторина по ПДД О чем говорят устаревшие слова?
О чем говорят устаревшие слова? Высший колледж. Успеваемость обучающихся 1 курса
Высший колледж. Успеваемость обучающихся 1 курса Образование как процесс, основные элементы образования
Образование как процесс, основные элементы образования Попутный газ
Попутный газ 9_5_Grazhdanskaya_Oborona_kak_sostavlyayuschaya_chast_natsionalnoy_bezopasnosti
9_5_Grazhdanskaya_Oborona_kak_sostavlyayuschaya_chast_natsionalnoy_bezopasnosti Виды, разрезы, сечения
Виды, разрезы, сечения Mayr Antriebstechnik i Mayr Polska – Германия, Польша.
Mayr Antriebstechnik i Mayr Polska – Германия, Польша. Сергей А. ЦыгановРоссийский фонд фундаментальных исследований
Сергей А. ЦыгановРоссийский фонд фундаментальных исследований Нестандартные двигатели
Нестандартные двигатели Устройство гранаты
Устройство гранаты Правовые основы физической культуры и спорта
Правовые основы физической культуры и спорта Яды в продуктах питания
Яды в продуктах питания Об особенностях ЕГЭ 2011года
Об особенностях ЕГЭ 2011года Мать – это женщина, которая...
Мать – это женщина, которая... Программа информатизации «Современная информационная среда гимназии как условие обеспечения преемственности дошкольного и нач
Программа информатизации «Современная информационная среда гимназии как условие обеспечения преемственности дошкольного и нач Литература 5 класс «Через урок - к правовому просвещению» Учитель Решетова Светлана Александровна
Литература 5 класс «Через урок - к правовому просвещению» Учитель Решетова Светлана Александровна “Роботизированный автодром”
“Роботизированный автодром” «ШАГ за ШАГом» МОУ средняя школа №4
«ШАГ за ШАГом» МОУ средняя школа №4 MIRRA PRO
MIRRA PRO Академическая гребля
Академическая гребля Предлоги 1
Предлоги 1 5 раунд
5 раунд