Слайд 2 Определение
Уравнение, содержащее переменную под знаком логарифма или в основании логарифма,

называется логарифмическим
Например, или
Если в уравнении содержится переменная не под знаком логарифма, то оно не будет являться логарифмическим.
Например,
Слайд 3 Самостоятельная работа № 1
Определите уравнения являющиеся логарифмическими и не являющимися

логарифмическими:
Слайд 4 Проверка самостоятельной работы
Являются логарифмическими
Не являются логарифмическими

Слайд 5 Найти х в следующих уравнениях (прокомментировать решение с места)

Слайд 6Самостоятельная работа № 2
Решить логарифмические уравнения:

Слайд 7 Проверка
самостоятельной работы № 2
Проверка:
4).Не является логарифмическим
Проверка:







 Money, Banking, and Financial Institutions
Money, Banking, and Financial Institutions Немой кинематограф. Вклад Александра Петровича Довженко
Немой кинематограф. Вклад Александра Петровича Довженко Проектирование и экспертиза образовательных систем
Проектирование и экспертиза образовательных систем Грибы-паразиты и меры борьбы с ними
Грибы-паразиты и меры борьбы с ними Права людини
Права людини Дизайн
Дизайн Управление собственностью. Стратегический менеджмент
Управление собственностью. Стратегический менеджмент культуры клеток
культуры клеток Перспективы ядерной энергетики
Перспективы ядерной энергетики Геометрические тела и окружающий мир
Геометрические тела и окружающий мир Творчество Евгения Рачёва
Творчество Евгения Рачёва Презентация на тему Промышленные загрязнения
Презентация на тему Промышленные загрязнения  Аналитика: Управленческая отчетность руководителя
Аналитика: Управленческая отчетность руководителя Здравствуй, школа!
Здравствуй, школа! Строевая подготовка
Строевая подготовка Мониторинг здоровья у занимающихся физической культурой − путь к успеху
Мониторинг здоровья у занимающихся физической культурой − путь к успеху Palkin_G_A_novaya
Palkin_G_A_novaya Пушкин "У лукоморья дуб зеленый"
Пушкин "У лукоморья дуб зеленый" Структура комплекса энтомофагов опыленной сливово-злаковой тли (Hyalopterus pruni) в условиях Беларуси
Структура комплекса энтомофагов опыленной сливово-злаковой тли (Hyalopterus pruni) в условиях Беларуси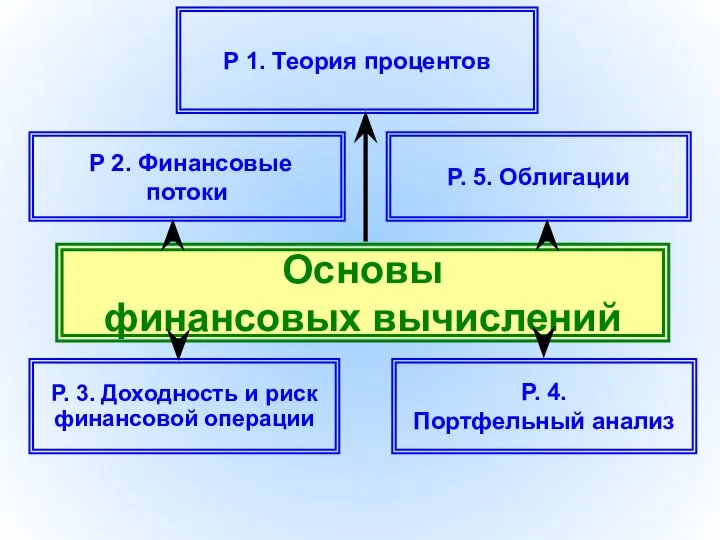 Основы финансовых вычислений
Основы финансовых вычислений Обучение работе с Microsoft Excel
Обучение работе с Microsoft Excel Буллинг в школе
Буллинг в школе Сокращение дробей
Сокращение дробей НАШИ БЛИЖАЙШИЕ СОСЕДИ
НАШИ БЛИЖАЙШИЕ СОСЕДИ Квалификационные требования к специалистам и проектным организациям в
Квалификационные требования к специалистам и проектным организациям в  Презентация на тему Стили речи
Презентация на тему Стили речи Косметическая линейка ватной продукции и влажных салфеток
Косметическая линейка ватной продукции и влажных салфеток Галактики. Многообразие галактик
Галактики. Многообразие галактик