Решение простейших тригонометрических уравнений

*
Чтобы успешно решать простейшие тригонометрические
уравнения необходимо следующее:
2) уметь определять значения синуса, косинуса,
тангенса и котангенса для точек числовой
окружности;
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и уметь отмечать их
на числовой окружности.
1) уметь отмечать точки на числовой
окружности;
3) знать свойства основных
тригонометрических функций;

Арксинусом числа
а называют такое число из отрезка
[- П/2; П/2], синус которого равен а.
arcsin а
П/2
- П/2
а
arcsin (-a)=-arcsin a
-а
-arcsin а
Арксинус и решение уравнений sin t=a.

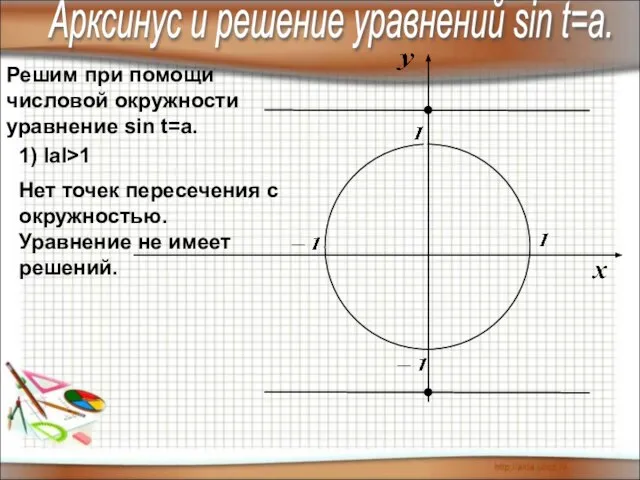
Решим при помощи
числовой окружности
уравнение sin t=a.
Арксинус и решение уравнений sin t=a.
1) IаI>1
Нет точек пересечения с окружностью.
Уравнение не имеет решений.

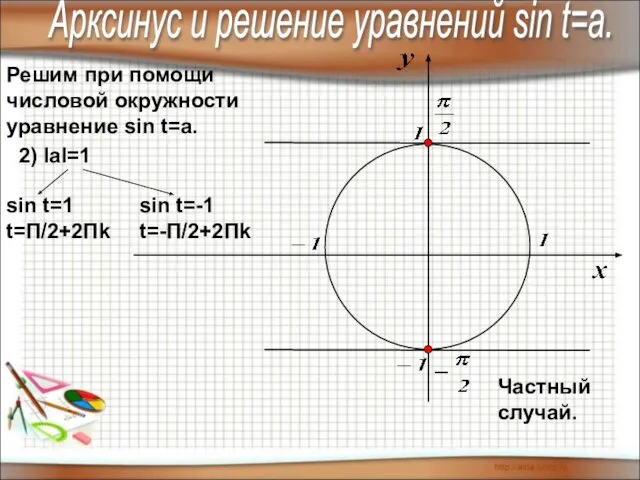
Решим при помощи
числовой окружности
уравнение sin t=a.
Арксинус и решение уравнений sin t=a.
2) IаI=1
sin t=1
t=П/2+2Пk
sin t=-1
t=-П/2+2Пk
Частный случай.

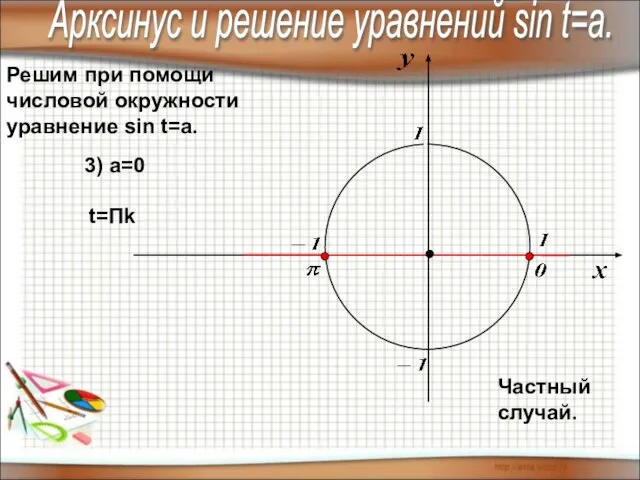
Решим при помощи
числовой окружности
уравнение sin t=a.
Арксинус и решение уравнений sin t=a.
3) а=0
t=Пk
Частный случай.

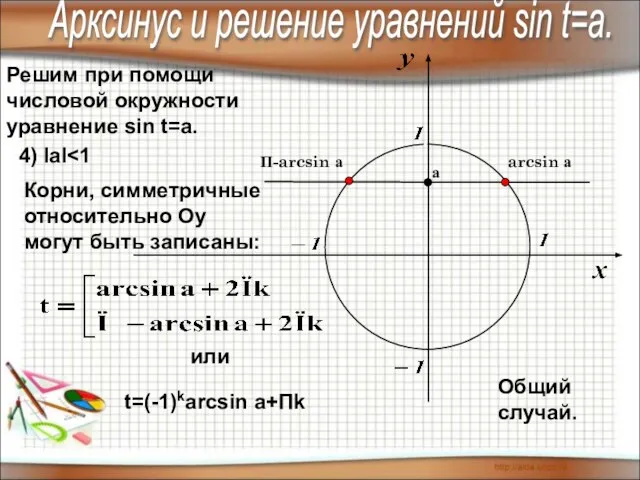
Решим при помощи
числовой окружности
уравнение sin t=a.
Арксинус и решение уравнений sin t=a.
4) IаI<1
Общий случай.
arcsin а
П-arcsin а
Корни, симметричные относительно Оу могут быть записаны:
t=(-1)karcsin a+Пk
или
а

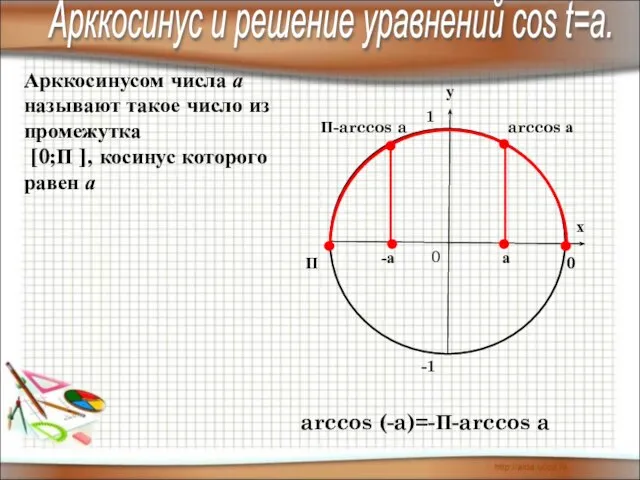
П
0
arccos а
Арккосинусом числа а называют такое число из промежутка
[0;П ], косинус которого равен а
а
arccos (-a)=-П-arccos a
-а
П-arccos a
Арккосинус и решение уравнений соs t=a.

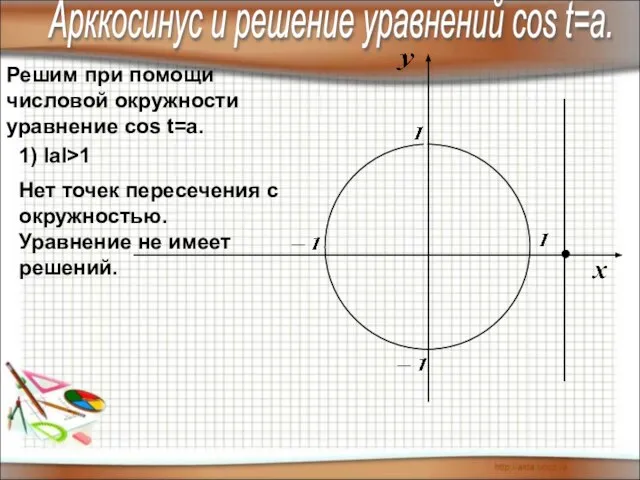
Решим при помощи
числовой окружности
уравнение cos t=a.
1) IаI>1
Нет точек пересечения с окружностью.
Уравнение не имеет решений.
Арккосинус и решение уравнений соs t=a.

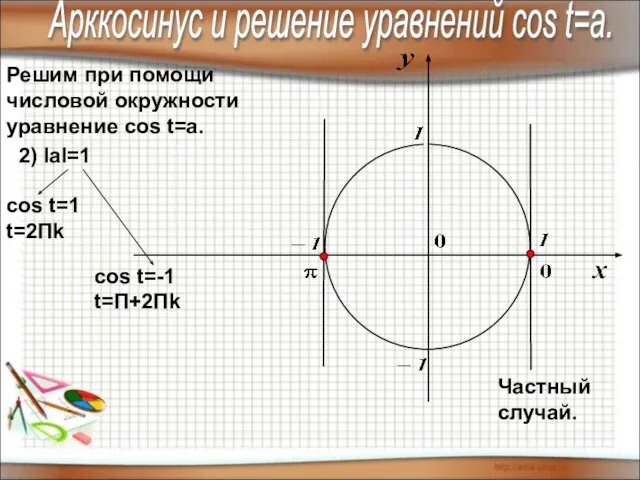
Решим при помощи
числовой окружности
уравнение cos t=a.
2) IаI=1
cos t=1
t=2Пk
cos t=-1
t=П+2Пk
Частный случай.
Арккосинус и решение уравнений соs t=a.

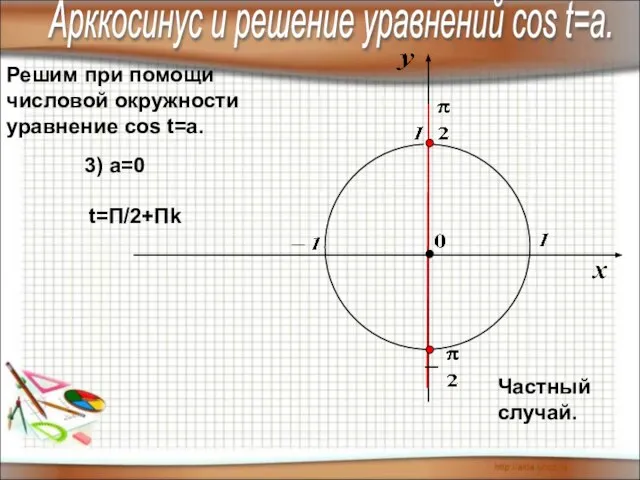
Решим при помощи
числовой окружности
уравнение cos t=a.
3) а=0
t=П/2+Пk
Частный случай.
Арккосинус и решение уравнений соs t=a.

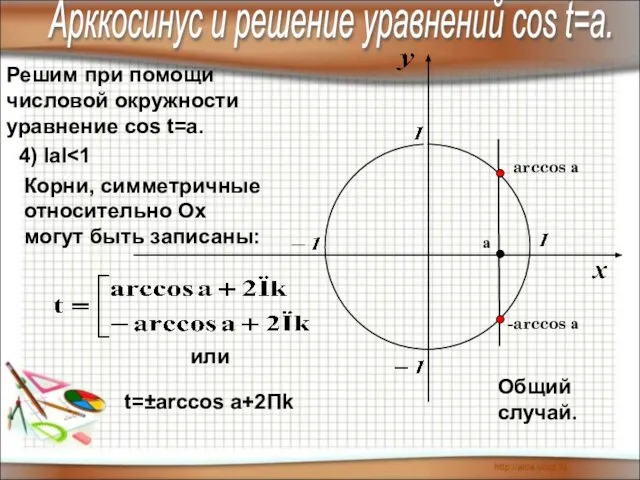
Решим при помощи
числовой окружности
уравнение cos t=a.
4) IаI<1
Общий случай.
arccos а
-arccos а
Корни, симметричные относительно Оx могут быть записаны:
t=±arccos a+2Пk
или
а
Арккосинус и решение уравнений соs t=a.

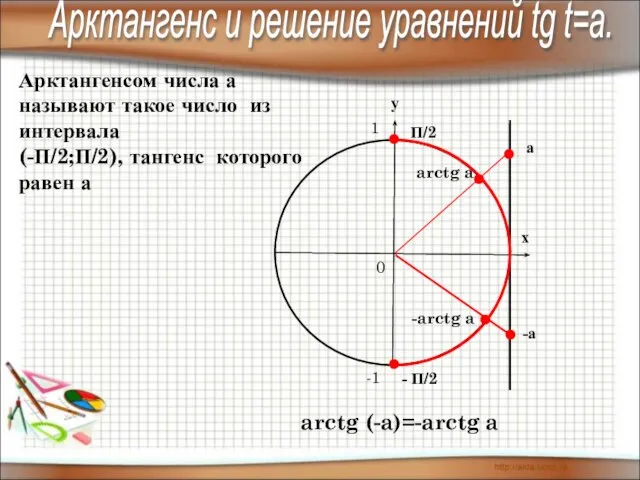
Арктангенсом числа а называют такое число из интервала
(-П/2;П/2), тангенс которого равен а
arctg a
а
П/2
- П/2
arctg (-a)=-arctg a
-а
-arctg a
Арктангенс и решение уравнений tg t=a.

*
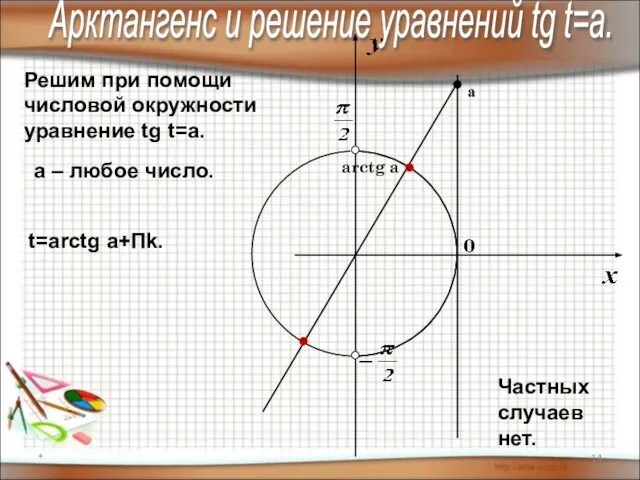
Арктангенс и решение уравнений tg t=a.
Решим при помощи
числовой окружности
уравнение tg t=a.
arctg a
а
a – любое число.
Частных случаев нет.
t=arctg a+Пk.

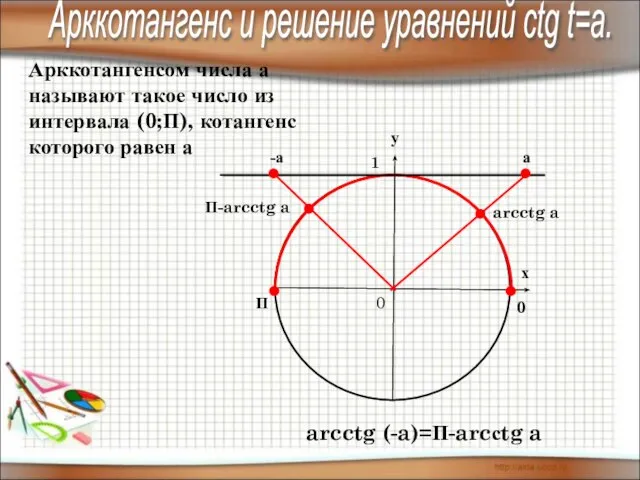
у
х
0
1
П
0
Арккотангенсом числа а называют такое число из интервала (0;П), котангенс которого равен а
-а
arcctg a
arcctg (-a)=П-arcсtg a
а
П-arcctg a
Арккотангенс и решение уравнений сtg t=a.

*
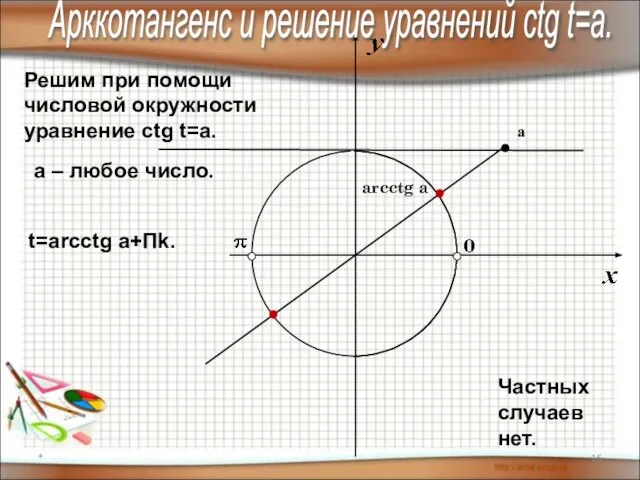
Решим при помощи
числовой окружности
уравнение сtg t=a.
arcctg a
а
a – любое число.
Частных случаев нет.
t=arcctg a+Пk.
Арккотангенс и решение уравнений сtg t=a.

Наша задача:
свести любое тригонометрическое уравнение
к простейшему виду.

Примеры уравнений.
Уравнение уже имеет простейший
вид , однако можно
применить формулы приведения и упростить его.
Это частный вид
уравнения cos t=a
a=0
Разделим обе части на 4.
О:
t
t

Характерная ошибка
Учащиеся делят обе части на 4
и получают следующее:
Грубая ошибка.

Уравнение переносом слагаемого и делением обеих частей легко сводится к простейшему.
Разделим обе части на 4.
О:
t
Примеры уравнений.

О:
Уравнение уже имеет простейший
вид
Это частный вид
уравнения cos t=a
a=0
Примеры уравнений.

О:
Уравнение уже имеет простейший
вид , однако,
можно использовать четность функции cos, применить формулы приведения и упростить его.
Примеры уравнений.

О:
Здесь уместно использовать формулу косинуса разности
аргументов:
Теперь уравнение
имеет простейший вид.
Решение удобнее разбить на два.
Примеры уравнений.

1 вариант
2 вариант
Потренируйся.