Содержание
- 2. Решение тригонометрических уравнений. МОУ СОШ №256 Г.Фокино sin x = 1 cos x = 0 sin
- 3. Проверочная работа. Каково будет решение уравнения cos x = a при а > 1
- 4. Проверочная работа. 5. В каком промежутке находится arccos a ? 5. В каком промежутке находится arcsin
- 5. Проверочная работа. 9. Каким будет решение уравнения cos x = 0? 9. Каким будет решение уравнения
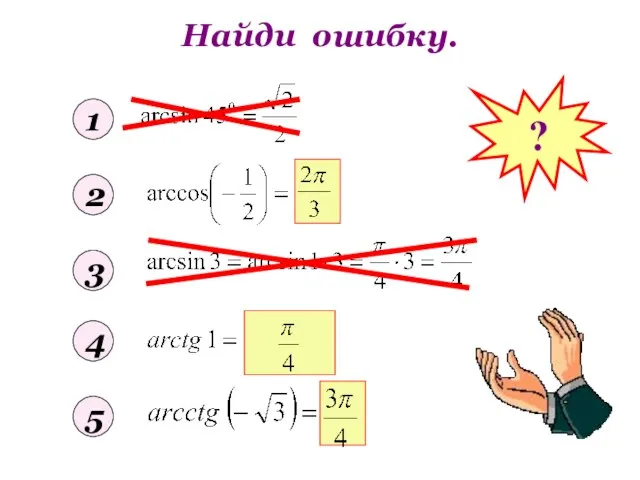
- 7. Найди ошибку. 1 2 3 4 5 ?
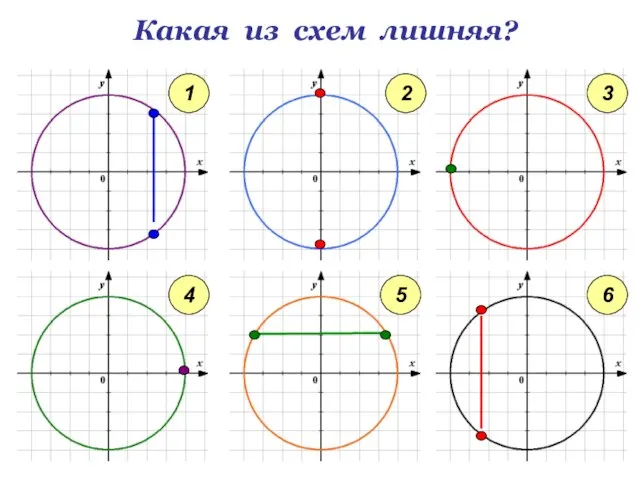
- 8. Какая из схем лишняя? 1 2 3 4 5 6
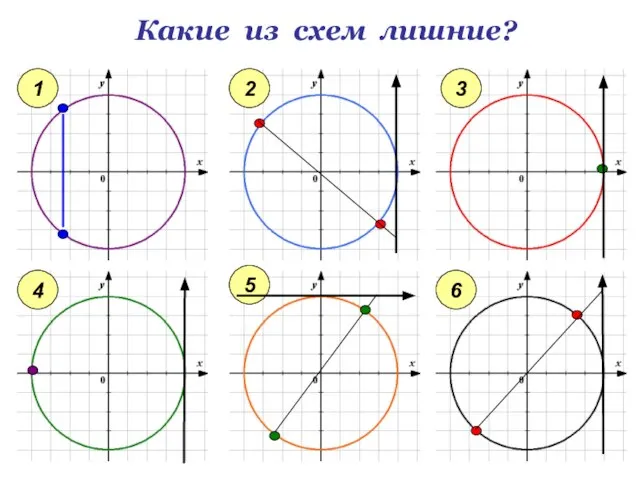
- 9. Какие из схем лишние? 1 2 3 4 5 6
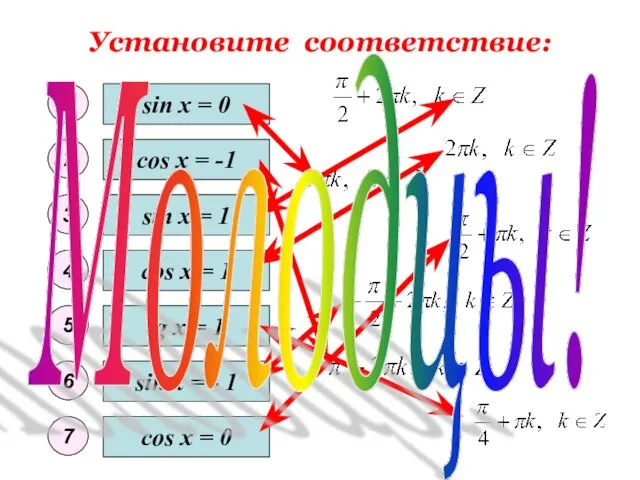
- 10. Установите соответствие: sin x = 0 sin x = - 1 sin x = 1 cos
- 11. Установите соответствие: sin x = 0 sin x = - 1 sin x = 1 cos
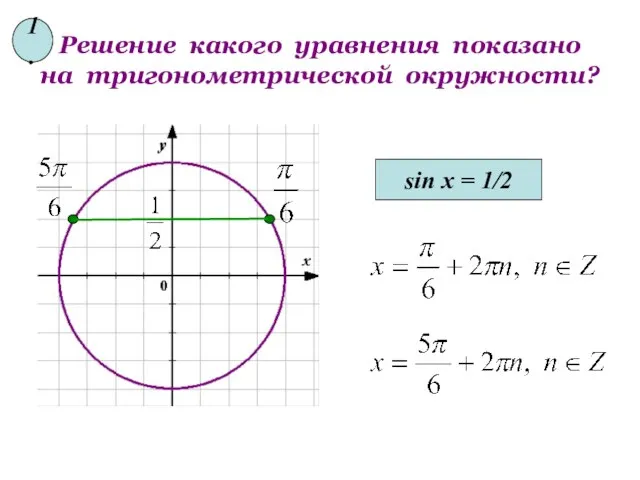
- 12. Решение какого уравнения показано на тригонометрической окружности? sin x = 1/2 1.
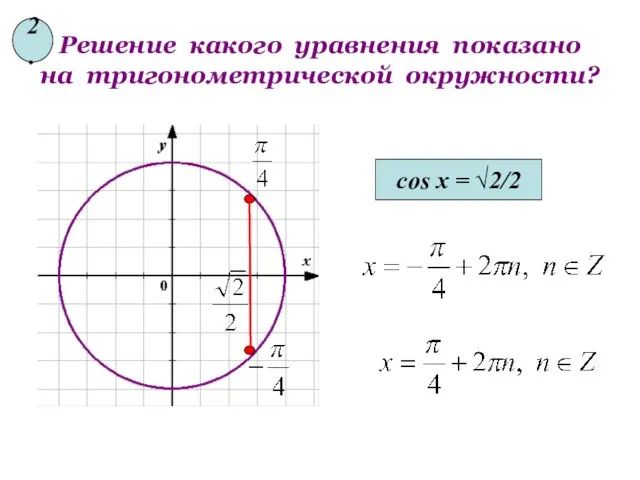
- 13. Решение какого уравнения показано на тригонометрической окружности? cos x = √2/2 2.
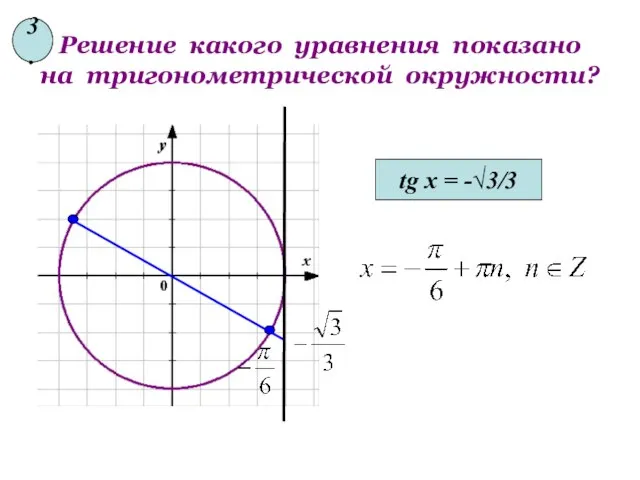
- 14. Решение какого уравнения показано на тригонометрической окружности? tg x = -√3/3 3.
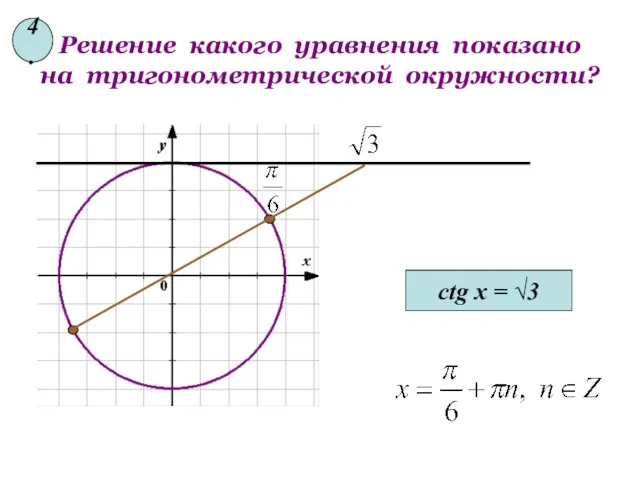
- 15. Решение какого уравнения показано на тригонометрической окружности? ctg x = √3 4.
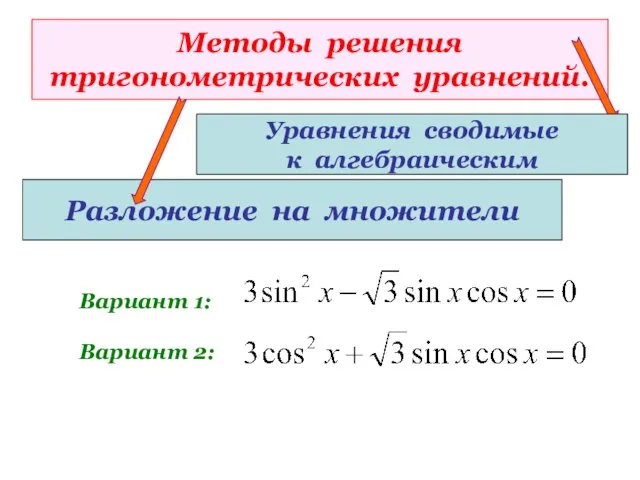
- 16. Методы решения тригонометрических уравнений. Уравнения сводимые к алгебраическим. Вариант 1: Вариант 2: Необходимо выбрать соответствующий прием
- 17. Методы решения тригонометрических уравнений. Разложение на множители Вариант 1: Вариант 2: Уравнения сводимые к алгебраическим
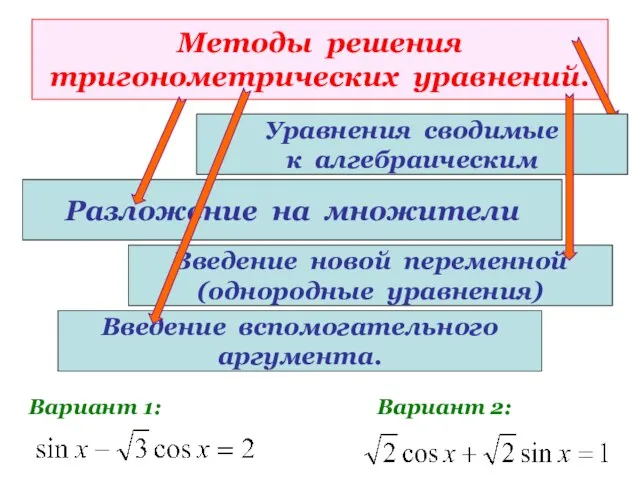
- 18. Методы решения тригонометрических уравнений. Разложение на множители Вариант 1: Вариант 2: Уравнения сводимые к алгебраическим Введение
- 19. Методы решения тригонометрических уравнений. Разложение на множители Вариант 1: Вариант 2: Уравнения сводимые к алгебраическим Введение
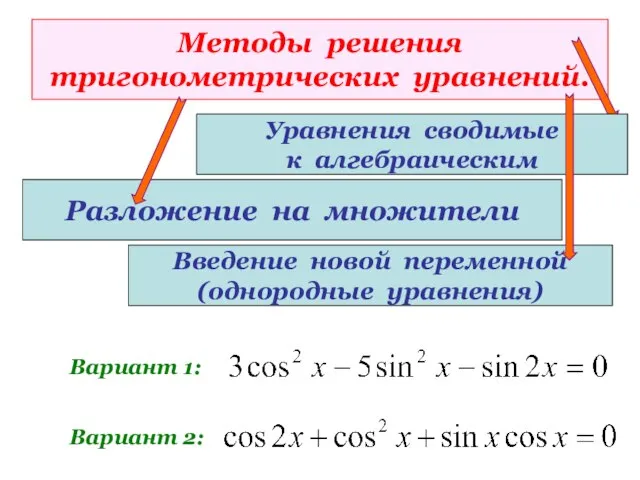
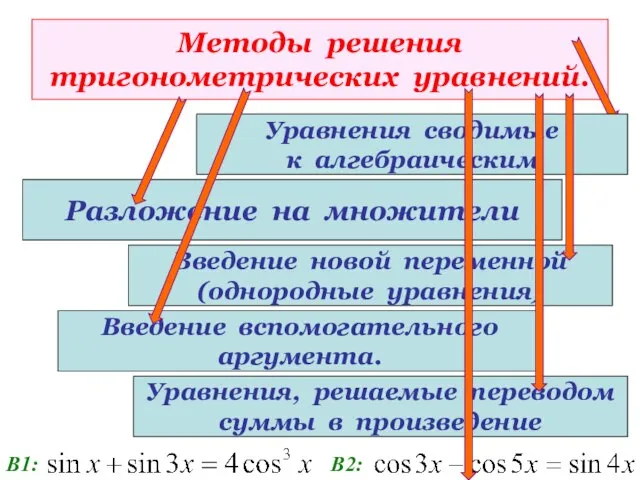
- 20. Методы решения тригонометрических уравнений. Разложение на множители Уравнения сводимые к алгебраическим Введение новой переменной (однородные уравнения)
- 21. Формулы квадрата половинных углов: Формулы понижения степени: Применение формул понижения степени. 2sin2 x + cos 4x
- 23. Скачать презентацию








 Необычный отель
Необычный отель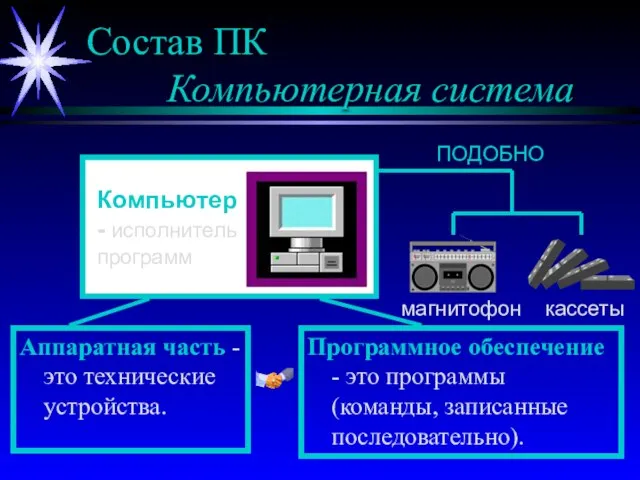 Состав ПК Компьютерная система
Состав ПК Компьютерная система 孔子学院在乌克兰和俄罗斯
孔子学院在乌克兰和俄罗斯 Places and Perspectives
Places and Perspectives Ресурси страховика
Ресурси страховика Метрическая система мер
Метрическая система мер Успешность адаптации ребенка при переходе со ступени начального образования – на основную
Успешность адаптации ребенка при переходе со ступени начального образования – на основную Istambek
Istambek Правила поведения итехники безопасности в кабинете информатики.
Правила поведения итехники безопасности в кабинете информатики. Город как среда обитания (5 класс)
Город как среда обитания (5 класс) Почему нужно чистить зубы?
Почему нужно чистить зубы? Автоматизированная система управления качеством вуза
Автоматизированная система управления качеством вуза Айдентика. Корпоративная идентификация
Айдентика. Корпоративная идентификация Повесть «Детство»
Повесть «Детство» Design Reboot
Design Reboot Клуб Алтын, доход посредством роста курса внутренней монеты
Клуб Алтын, доход посредством роста курса внутренней монеты Перспективы участия иностранных банков в развитии ритейлового бизнеса в российских регионах
Перспективы участия иностранных банков в развитии ритейлового бизнеса в российских регионах Работа с заданиями на анализ исторических версий и оценок.
Работа с заданиями на анализ исторических версий и оценок. Подготовка к ЕГЭ. (окончания глаголов и суффиксов причастий)
Подготовка к ЕГЭ. (окончания глаголов и суффиксов причастий) Проблемы начала правоприменения в сфере борьбы с картелями – опыт Бразилии
Проблемы начала правоприменения в сфере борьбы с картелями – опыт Бразилии Сложноподчиненные предложения с определительными придаточными
Сложноподчиненные предложения с определительными придаточными Фразеологическое ядро старославянского языка
Фразеологическое ядро старославянского языка План развития ЮФО 2020
План развития ЮФО 2020 Конструктивизм
Конструктивизм Мартиничка
Мартиничка Электронное портфолио ученика
Электронное портфолио ученика Магистерская программа 031100.68.20 Сопоставительное изучение культур и межкультурная коммуникация
Магистерская программа 031100.68.20 Сопоставительное изучение культур и межкультурная коммуникация Презентация на тему Украшение пасхального яйца
Презентация на тему Украшение пасхального яйца