Содержание
- 2. Содержание. Вводная часть, повторение теоретического материала. Решение тригонометрических уравнений. Проблемы, возникающие при решении тригонометрических уравнений.
- 3. ЦЕЛЬ: Повторить решение тригонометрических уравнений. 1. Знать формулы для решения простейших тригонометрических уравнений. 2. Различать типы
- 4. Устная работа. Решите уравнения А) 3 х – 5 = 7 Б) х2 – 8 х
- 5. Устная работа Упростите выражения А) (sin a – 1) (sin a + 1) Б) sin2 a
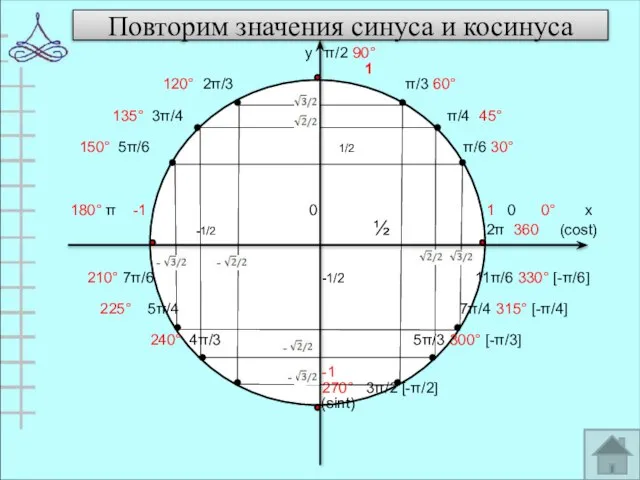
- 6. Повторим значения синуса и косинуса у π/2 90° 1 120° 2π/3 π/3 60° 135° 3π/4 π/4
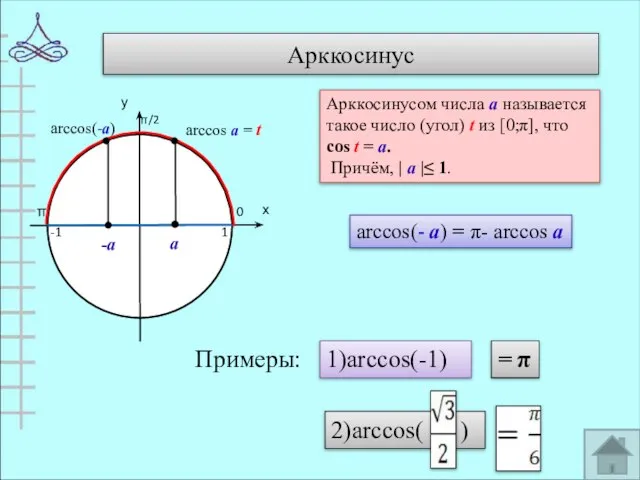
- 7. Арккосинус 0 π 1 -1 arccos(-а) Арккосинусом числа а называется такое число (угол) t из [0;π],
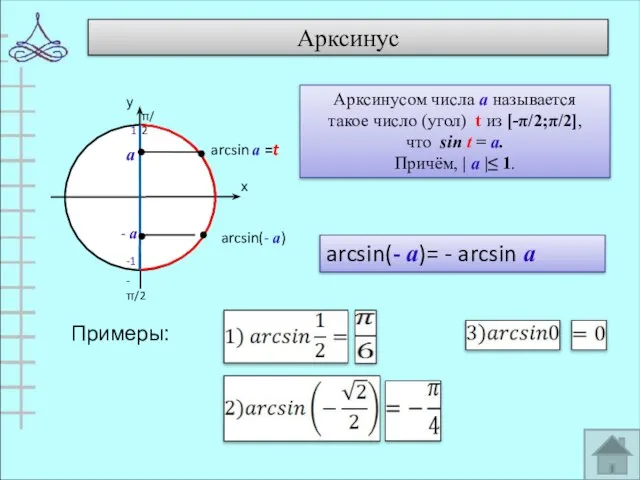
- 8. Арксинус Примеры: а - а arcsin(- а)= - arcsin а Арксинусом числа а называется такое число
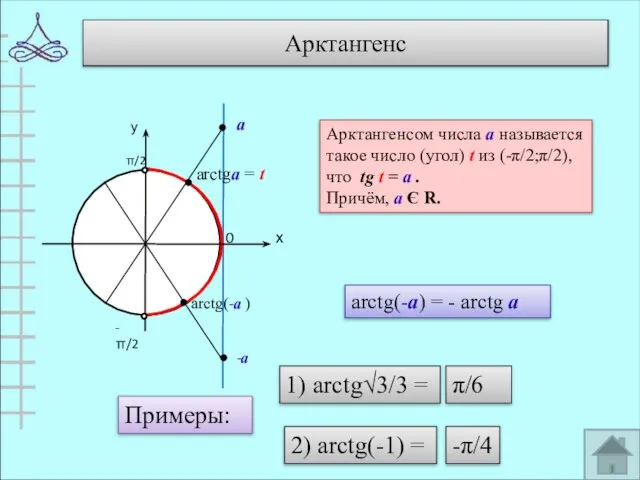
- 9. Арктангенс 0 arctgа = t Арктангенсом числа а называется такое число (угол) t из (-π/2;π/2), что
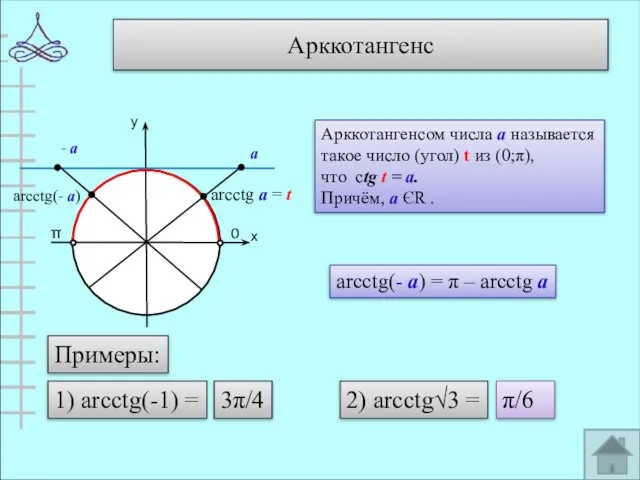
- 10. Арккотангенс у х 0 π arcctg а = t Арккотангенсом числа а называется такое число (угол)
- 11. Повторение 1 вариант sin (-π/3) cos 2π/3 tg π/6 ctg π/4 cos (-π/6) sin 3π/4 arcsin
- 12. Повторение Ответы 1 вариант - √3/2 - 1/2 √3/3 1 √3/2 √2/2 π/4 0 - π/6
- 13. Формулы корней простейших тригонометрических уравнений 1.cost = а , где |а| ≤ 1 или Частные случаи
- 14. Формулы корней простейших тригонометрических уравнений 2. sint = а, где | а |≤ 1 или Частные
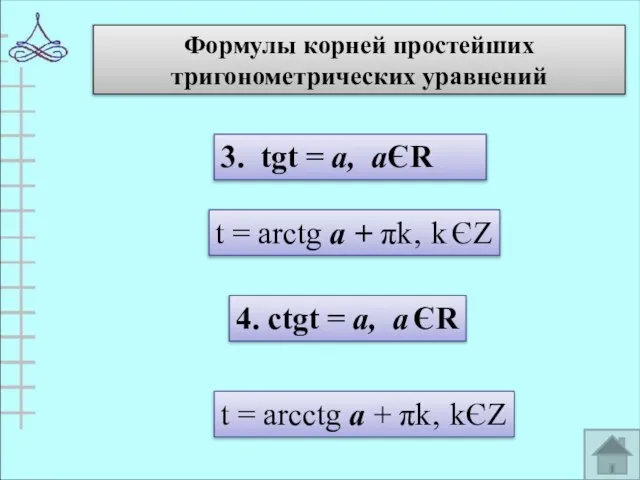
- 15. Формулы корней простейших тригонометрических уравнений 3. tgt = а, аЄR t = arctg а + πk‚
- 16. При каких значениях х имеет смысл выражение: 1.arcsin(2x+1) 2.arccos(5-2x) 3.arccos(x²-1) 4.arcsin(4x²-3x) 1) -1≤ 2х+1 ≤1 -2≤
- 17. Примеры: cost= - ; 2) sint = 0; 3) tgt = 1; t= ±arccos(-1/2)+2πk, kЄZ t=
- 18. Решение простейших уравнений tg2x = -1 2x = arctg (-1) + πk, kЄZ 2x = -π/4
- 19. Виды тригонометрических уравнений 1.Сводимые к квадратным Решаются методом введения новой переменной a∙sin²x + b∙sinx + c=0
- 20. 2.Однородные 1)Первой степени: Решаются делением на cos х (или sinx) и методом введения новой переменной. a∙sinx
- 21. 2) Однородные уравнения второй степени: Решаются делением на cos² х (или sin²x) и методом введения новой
- 22. Виды тригонометрических уравнений 3. Уравнение вида: А sinx + B cosx = C. А, В, С
- 23. Виды тригонометрических уравнений 4. Решение тригонометрических уравнений с помощью универсальной тригонометрической подстановки Решаются с помощью введения
- 24. Формулы. Универсальная подстановка. х ≠ π + 2πn; Проверка обязательна! Понижение степени. = (1 + cos2x
- 25. Правила. Увидел квадрат – понижай степень. Увидел произведение – делай сумму. Увидел сумму – делай произведение.
- 26. 1.Потеря корней: делим на g(х). опасные формулы (универсальная подстановка). Этими операциями мы сужаем область определения. 2.
- 27. Решение тригонометрических уравнений по известным алгоритмам Вариант 1. На «3» 3 sin x+ 5 cos x
- 29. Скачать презентацию




















 Математику уже затем учить надо, что она ум в порядок приводит
Математику уже затем учить надо, что она ум в порядок приводит Истинные образы. Ложные образы
Истинные образы. Ложные образы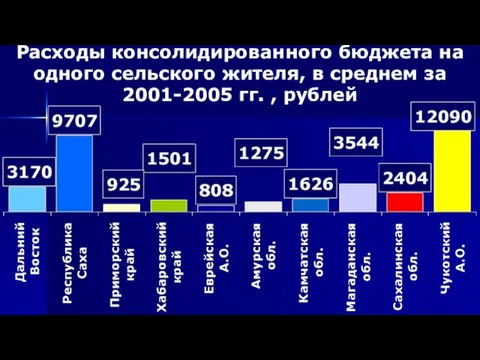 Расходы консолидированного бюджета на одного сельского жителя, в среднем за 2001-2005 гг. , рублей
Расходы консолидированного бюджета на одного сельского жителя, в среднем за 2001-2005 гг. , рублей Второй Всероссийский чемпионат по дебатамПолуфинал
Второй Всероссийский чемпионат по дебатамПолуфинал Practical Phonetics
Practical Phonetics Иҗек
Иҗек Иконопись в Древней Руси
Иконопись в Древней Руси История военной песни
История военной песни Презентация на тему Опасные места
Презентация на тему Опасные места Наука и искусство Художник и ученый
Наука и искусство Художник и ученый Philip Morris. Экспертиза, проекты, услуги
Philip Morris. Экспертиза, проекты, услуги Создай свою компьютерную сеть
Создай свою компьютерную сеть Борьба с трансграничной преступностью
Борьба с трансграничной преступностью Метрологическая надежность, поверка и калибровка средств измерений (СИ)
Метрологическая надежность, поверка и калибровка средств измерений (СИ) «ОБУЧЕНИЕ МЕЖКУЛЬТУРНОМУ ДИАЛОГУ КАК СРЕДСТВО ФОРМИРОВАНИЯ ГРАЖДАНСКОЙ СОЛИДАРНОСТИ, КУЛЬТУРЫ МИРА И СОГЛАСИЯ»
«ОБУЧЕНИЕ МЕЖКУЛЬТУРНОМУ ДИАЛОГУ КАК СРЕДСТВО ФОРМИРОВАНИЯ ГРАЖДАНСКОЙ СОЛИДАРНОСТИ, КУЛЬТУРЫ МИРА И СОГЛАСИЯ» Михаил Тимофеевич Калашников
Михаил Тимофеевич Калашников Старое и новое о круге
Старое и новое о круге SP_Osen_2022_Izh
SP_Osen_2022_Izh Племенные союзы на территории Казахстана
Племенные союзы на территории Казахстана  Контрольная работа
Контрольная работа ОАО «БАШИНФОРМСВЯЗЬ»ПРЕДСТАВЛЯЕТУСЛУГИ ИНТЕЛЛЕКТУАЛЬНОЙ СЕТИДЛЯ РАЗВИТИЯ ВАШЕГО БИЗНЕСА
ОАО «БАШИНФОРМСВЯЗЬ»ПРЕДСТАВЛЯЕТУСЛУГИ ИНТЕЛЛЕКТУАЛЬНОЙ СЕТИДЛЯ РАЗВИТИЯ ВАШЕГО БИЗНЕСА Татьяна Малева Оксана Синявская Вновь кризис пенсионной системы?
Татьяна Малева Оксана Синявская Вновь кризис пенсионной системы? Процесс транснационализации и ТНК в мировой экономике
Процесс транснационализации и ТНК в мировой экономике Коммерческое_предложение_Кедди_для_экспорта_
Коммерческое_предложение_Кедди_для_экспорта_ Ядерное, химическое и биологическое оружие
Ядерное, химическое и биологическое оружие Презентация на тему Основные инструменты формирования служебно-профессиональной морали и нравственности культуры государственн
Презентация на тему Основные инструменты формирования служебно-профессиональной морали и нравственности культуры государственн Конструирование текстов, предложений (2 класс)
Конструирование текстов, предложений (2 класс) Программа. Пушкинкая карта_инструкция
Программа. Пушкинкая карта_инструкция