Содержание
- 2. Самостоятельная работа Вариант 1 Дайте определение, что число a больше числа b Сравните: а) б) а2
- 3. Теорема 1 Если а>b, то b Если а a Теорема 2 Если а Теорема 3 Если
- 4. Если a и b положительные числа и a Пример 1 Оцените периметр квадрата со стороной a
- 5. В классе №748 № 731 № 749(г) №750 - № 754 (в,г) д/з п29 №749 -
- 6. 1. Если a > b и b > c , то a > c. Например, 6
- 7. a b 4. Если a > b и c > 0 , то ac > bc
- 8. 5. Если a > b и c > d, то a + c > b +
- 11. Скачать презентацию
Слайд 2Самостоятельная работа
Вариант 1
Дайте определение, что число a больше числа b
Сравните: а)
Самостоятельная работа
Вариант 1
Дайте определение, что число a больше числа b
Сравните: а)

Докажите неравенство (а – 3)(а + 9 ) < (а+3)(а + 5)
Вариант 2
Дайте определение, что число a меньше числа b
Сравните: а) б) а2 + 25 и 10а
Докажите неравенство (а – 2)(а + 9 ) < (а+3)(а + 4)
Слайд 3Теорема 1 Если а>b, то b Если аa
Теорема 2 Если
Теорема 1 Если а>b, то b Теорема 2 Если

Теорема 3 Если а < b и c – любое число, то a + с < b + c
Теорема 4 Если а < b и c – положительное число, то a * с < b * c
Если а < b и c – отрицательное число, то a * с > b * c
Слайд 4Если a и b положительные числа и a < b, то
Пример
Если a и b положительные числа и a < b, то
Пример
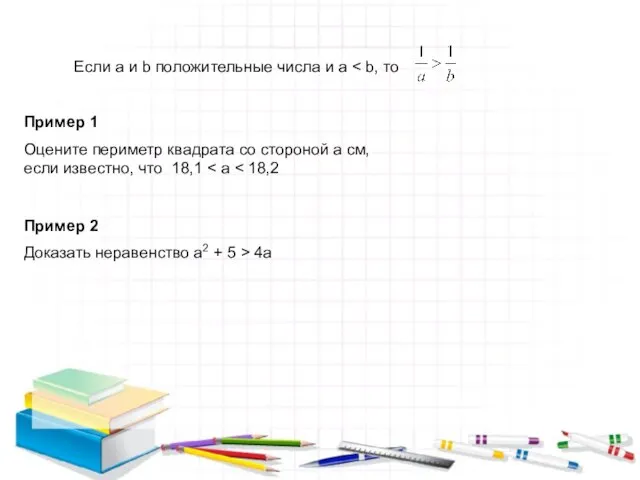
Оцените периметр квадрата со стороной a см, если известно, что 18,1 < a < 18,2
Пример 2
Доказать неравенство a2 + 5 > 4a
Слайд 61. Если a > b и b > c , то a
1. Если a > b и b > c , то a

Например, 6 > 4 и 4 > -1, тогда 6 > -1.
Аналогично, если c < b и b < a , то c < a.
2. Если a > b, то a + c > b + c.
Если к обеим частям неравенства прибавить одно и то же число
(положительное или отрицательное), то знак неравенства не
изменится.
Например, 6 > 4, тогда 6 + 3 > 4 + 3.
3. Если a + c > b, то a > b - c.
Любое слагаемое можно переносить из одной части неравенства
в другую, изменяя при этом знак слагаемого на противоположный.
Например, 5 + 10 > 4, тогда 5 > 4 – 10.
Слайд 7a b
4. Если a > b и c > 0 , то
a b
4. Если a > b и c > 0 , то

c c
Если обе части неравенства умножить или разделить на одно и
то же положительное число, то знак неравенства не изменится.
Например, 3 > 1, тогда 3 ∙ 5 > 1 ∙ 5.
7 < 21, тогда 7 : 7 < 21 : 7.
a b
Если a > b и c < 0, то ac < bc и .
c c
Если обе части неравенства умножить или разделить на одно и
то же отрицательное число, то знак неравенства изменится на
противоположный.
Например, 9 > 4, тогда 9 ∙ (-2) < 4 ∙ (-2).
12 < 30, тогда 12 : (-3) > 30 : (-3).
Слайд 85. Если a > b и c > d, то a +
5. Если a > b и c > d, то a +

При сложении неравенств одинакового знака получается
неравенство того же знака.
Например, 8 > 5 и 4 > 1, тогда 8 + 4 > 5 + 1.
6. Если для положительных чисел a, b, c, d: a > b и c > d, то
a ∙ c > b ∙ d.
При умножении неравенств одинакового знака, у которых левые и
правые части положительны, получается неравенство того же
знака.
Например, 12 > 5 и 3 > 2, тогда 12 ∙ 3 > 5 ∙ 2.


 ДЦП
ДЦП  Презентация на тему Лишайники, водоросли, мхи
Презентация на тему Лишайники, водоросли, мхи Тактика поведения в сложных ситуациях взаимодействия
Тактика поведения в сложных ситуациях взаимодействия Драма как род литературы
Драма как род литературы Презентация на тему Раскрытие скобок
Презентация на тему Раскрытие скобок  RTV 133
RTV 133 Болезни зубов
Болезни зубов Развитие орфографической зоркости у младших школьников
Развитие орфографической зоркости у младших школьников Презентация на тему Синергетика
Презентация на тему Синергетика  Черное и белое духовенство
Черное и белое духовенство Теории происхождения права
Теории происхождения права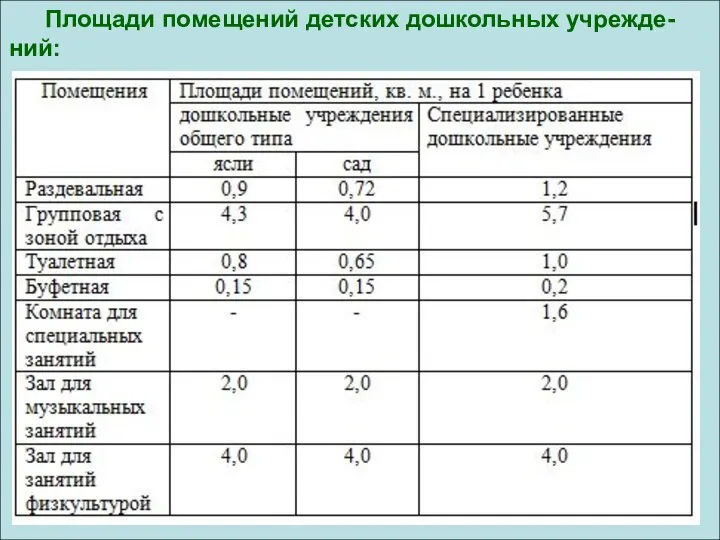 Площади помещений детских дошкольных учреждений
Площади помещений детских дошкольных учреждений Характеристика перцептивной стороны общения
Характеристика перцептивной стороны общения 1-й квест
1-й квест Курс CMS Wordpress. Практика. Выбор тематики своего сайта
Курс CMS Wordpress. Практика. Выбор тематики своего сайта Подростковые и молодежные субкультуры XXI века
Подростковые и молодежные субкультуры XXI века Мини-музей "Югра"
Мини-музей "Югра" Исследовательская краеведческая работа ученика 11 «А» класса Андреевской СОШ Судогодского района Владимирской области Воронин
Исследовательская краеведческая работа ученика 11 «А» класса Андреевской СОШ Судогодского района Владимирской области Воронин Методика Масару Ибука
Методика Масару Ибука Структура современного урока. Роль мотивации и рефлексии в учебном процессе
Структура современного урока. Роль мотивации и рефлексии в учебном процессе Как оформить инвестиции: от простого к сложному
Как оформить инвестиции: от простого к сложному Использование национально-регионального компонента в обучении химии на элективных курсах
Использование национально-регионального компонента в обучении химии на элективных курсах Дистанция в заданном направлении
Дистанция в заданном направлении Животные долгожители
Животные долгожители Здравствуй, Зимушка-Зима!
Здравствуй, Зимушка-Зима! Методы генной инженерии
Методы генной инженерии ВИРТУАЛЬНАЯ ЛЕКСИКОГРАФИЧЕСКАЯ ЛАБОРАТОРИЯ ДЛЯ ТОЛКОВЫХ СЛОВАРЕЙ VIRTUAL LEXICOGRAPHICAL LABORATORY FOR EXPLANATORY DICTIONARIES Остапова И. В. (
ВИРТУАЛЬНАЯ ЛЕКСИКОГРАФИЧЕСКАЯ ЛАБОРАТОРИЯ ДЛЯ ТОЛКОВЫХ СЛОВАРЕЙ VIRTUAL LEXICOGRAPHICAL LABORATORY FOR EXPLANATORY DICTIONARIES Остапова И. В. ( Технология проблемного обучения на уроках русского языка
Технология проблемного обучения на уроках русского языка