Содержание
- 2. При решении заданий С3 обязательным условием является создание дерева решений, а также умение сделать правильный вывод
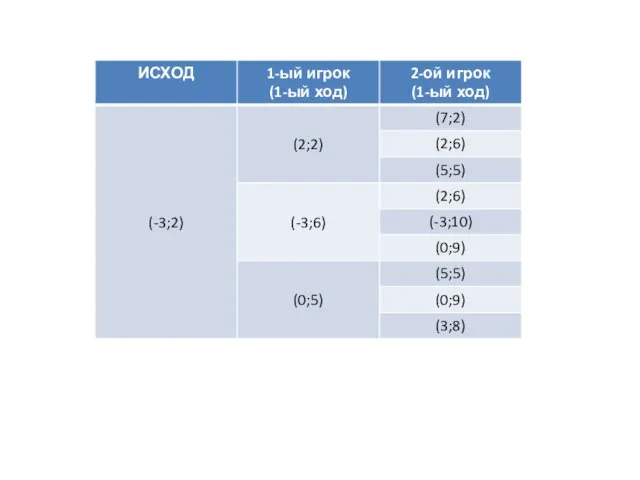
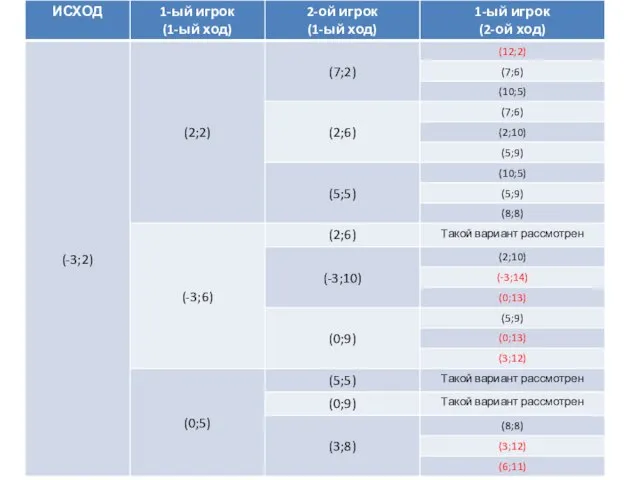
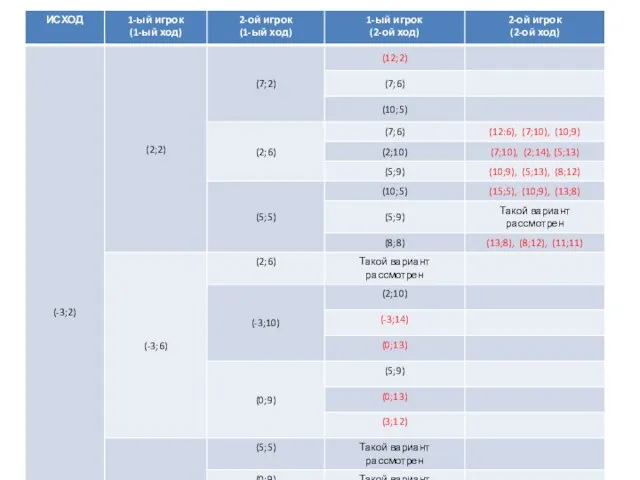
- 3. Рассмотрим задачу: Два игрока играют в игру. На координатной плоскости в точке с координатами (-3;2) стоит
- 4. Помним о том, что выигрывает игрок, после хода которого расстояние от фишки до начала координат будет
- 8. Вывод: Выиграет второй игрок при любом ходе первого игрока, если первый ход второго игрока будет (2;6)
- 9. Пример 1 Пример 2
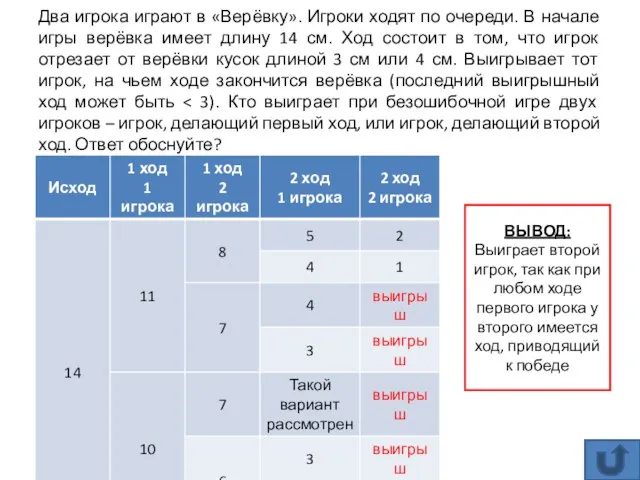
- 10. Два игрока играют в «Верёвку». Игроки ходят по очереди. В начале игры верёвка имеет длину 14
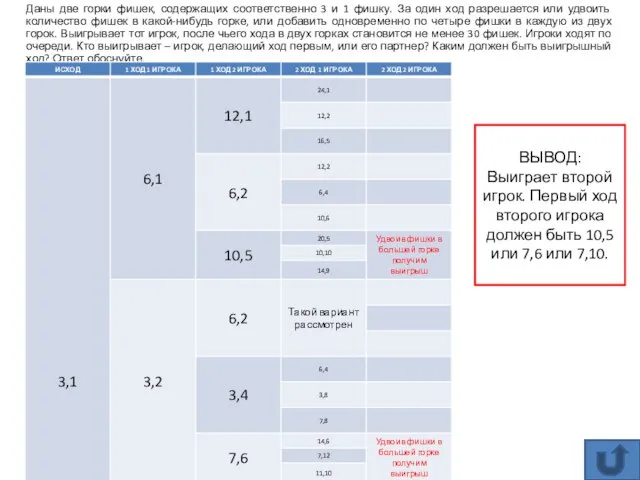
- 11. Даны две горки фишек, содержащих соответственно 3 и 1 фишку. За один ход разрешается или удвоить
- 12. Спасибо за внимание!
- 14. Скачать презентацию






 Реформа языка Карамзина
Реформа языка Карамзина Варианты расчета бонуса за два месяца
Варианты расчета бонуса за два месяца Эксплуатация автомобильного транспорта
Эксплуатация автомобильного транспорта Государство в политической системе
Государство в политической системе ИСТОРИЯ СПИЧЕК
ИСТОРИЯ СПИЧЕК Презентация на тему Растения-индикаторы
Презентация на тему Растения-индикаторы Мышление как психический процесс. Виды и формы мышления. 4 формата мышления
Мышление как психический процесс. Виды и формы мышления. 4 формата мышления Субъекты правовых отношений. Правовое положение лиц
Субъекты правовых отношений. Правовое положение лиц скульптура «Под одними звездами» ("Unter den gleichen Sternen")
скульптура «Под одними звездами» ("Unter den gleichen Sternen") Виды гимнастики
Виды гимнастики Hilton Hotels & Resorts
Hilton Hotels & Resorts Шар. Елка. Снеговик
Шар. Елка. Снеговик Обзор православной литературы Доброе слово для малых ребят
Обзор православной литературы Доброе слово для малых ребят Водные маршруты
Водные маршруты Презентация на тему Василий Тёркин
Презентация на тему Василий Тёркин  Технология приготовления пиццы
Технология приготовления пиццы Мир в свечах Выполнила: Плаксунова Людмила МОУ СОШ №4 Руководитель: Чуприна Т.В.
Мир в свечах Выполнила: Плаксунова Людмила МОУ СОШ №4 Руководитель: Чуприна Т.В. "Поле - чудес" по произведениям К.И. Чуковского
"Поле - чудес" по произведениям К.И. Чуковского PURE_THERAPY_Bezuprechnaya_idealno_ochischennaya_kozha
PURE_THERAPY_Bezuprechnaya_idealno_ochischennaya_kozha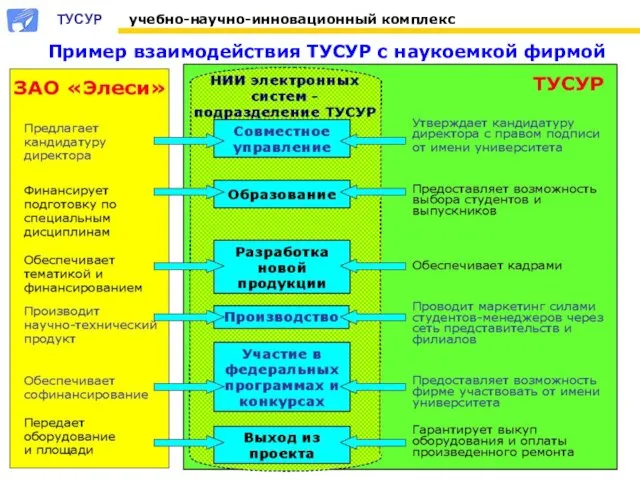 Пример взаимодействия ТУСУР с наукоемкой фирмой
Пример взаимодействия ТУСУР с наукоемкой фирмой Введение в менеджмент
Введение в менеджмент Австралия
Австралия Who should be the first ?
Who should be the first ? Велосипедный туризм
Велосипедный туризм Музей восстания машин
Музей восстания машин Презентация "Художники пореформенной России" - скачать презентации по МХК
Презентация "Художники пореформенной России" - скачать презентации по МХК Хочу отдыхать
Хочу отдыхать Сенситивные периоды человека (методика Марии Монтессори)
Сенситивные периоды человека (методика Марии Монтессори)