Счастливый случай

Применение
непрерывности и производной

Разработчик:
учитель математики МОУ СОШ №84 города Краснодара
Сивохо
Римма Васильевна

Тип урока
Урок обобщающего повторения и систематизации знаний.
Учебные задачи:
учить обобщать и систематизировать полученные знания;
учить использовать компьютерные технологии для устной самостоятельной работы с целью проверки усвоения теории по данной теме;
учить применять полученные теоретические знания для решения задач;
учить анализировать условие задачи с тем, чтобы выбрать оптимальный вариант решения;
осуществлять контроль своих знаний с помощью компьютерных тестов.

Развивающие задачи:
способствовать развитию общеучебных умений;
развивать творческую сторону мышления;
учить осуществлять исследовательскую деятельность;
развивать уверенность в себе, интерес к предмету.
Воспитательные задачи:
воспитывать потребность в знаниях;
формировать навыки умственного труда – поиск рациональных путей решения, самообразования, самовоспитания;
воспитывать культуру общения, взаимопомощь, умение слушать товарища; ответственность.
Форма урока
Урок – игра

Оборудование урока:
ПК учителя, мультимедийный проектор, персональные компьютеры учащихся.
Индивидуальные карточки для проверки домашнего задания.
Презентация, содержащая материал для повторения и закрепления теоретических знаний, для фронтального опроса по теории.
Компьютерное тестирование (самостоятельная работа на 4 варианта, автор Сивохо Р.В. с использованием VIP Test (ver.2.4)) для отработки навыков практического применения теории к решению упражнений, для самоконтроля,
Слайд, содержащий краткие исторические сведения.

« …Учиться можно только весело…
Чтобы переварить знания. Надо поглощать их с аппетитом…».
Франс А.

В данной функции от х, нареченной игреком, y = f(x)
Вы фиксируете икс, отмечая индексом. хо , f(xо )
Придаете вы ему тотчас приращение, xо + ∆x
Тем у функции самой вызвав изменение. ∆y = f(xо + ∆x) -f (xо)
Приращений тех теперь взявши отношение, ∆y : ∆x
Пробуждаете к нулю у ∆x стремление. ∆x → 0
Ответ такого отношенья вычисляется,
Он производною в науке называется. y′ = ∆y : ∆x при ∆x → 0

"Спешите видеть"
"Дальше"
"Заморочки
из бочки"
"Темная лошадка"

1. Переменная величина, значение которой зависит от изменения другой величины…
(функция)
2. Производная от координаты по времени есть … (скорость)
3. Вид числового промежутка…
(интервал)
4. Пример функции непрерывной, но не дифференцируемой в данной точке
(y = |x|)
5. Геометрический смысл производной…
( f ′(x) = tg α = k )
6. Для функции y = kx + b, k – это …
(угловой коэффициент прямой)
7. Каким по виду будет угол между касательной к графику функции в точке с абсциссой х0 и положительным направлением оси ОХ, если f ,(x) > 0?
(острый)
"Дальше"
Вопросы 1-ой команде

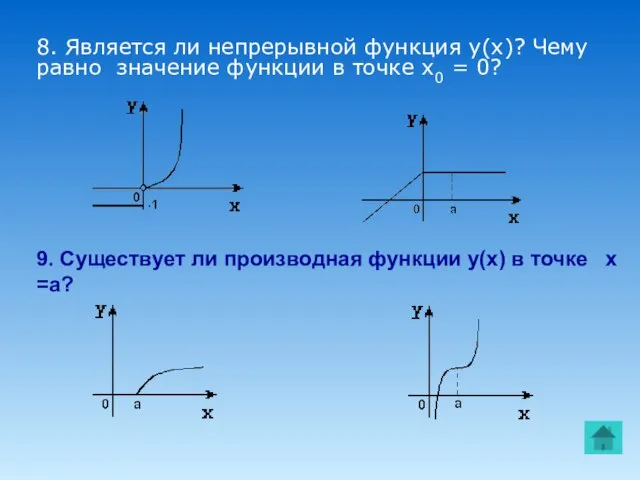
8. Является ли непрерывной функция y(x)? Чему равно значение функции в точке х0 = 0?
9. Существует ли производная функции y(x) в точке х = а?

1. Физический смысл производной в точке…
(скорость как производная от перемещения по времени)
2. Величина, которая может принимать различные значения…
(переменная)
3. Производная от скорости по времени есть …
(ускорение)
4. Если на интервале (a;b) функция f непрерывна и не обращается в нуль, то она на этом интервале …
(сохраняет знак)
5. Элемент области определения функции …
(аргумент)
6. Два алгебраических выражения, соединенных знаком > или <…
(неравенство)
7. Каким по виду будет угол между касательной к графику функции в точке с абсциссой х и положительный направлением оси ох, если f′(x) < 0?
(тупым)
"Дальше"
Вопросы 2-ой команде

9. Существует ли производная функции y(x) в точке х =а?
8. Является ли непрерывной функция y(x)? Чему равно значение функции в точке х0 = 0?

Великий немецкий ученый. Философ, математик, физик, юрист, языковед. Создатель наряду с Ньютоном математического анализа. Именно они открыли дифференциальное и интегральное исчисление. Этот ученый является основоположником большой математической школы. Его идеи оказали значительное влияние на развитие математической логики.

«Весь мир его узнал по изданным трудам,
Был даже край родной с ним вынужден считаться;
Уроки мудрости давал он мудрецам,
Он был мудрее их: умел он сомневаться…»
Вольтер
Лейбниц

Исторические сведения
Дифференциальное исчисление создано Ньютоном и Лейбницем в конце 17 столетия. Понятие производной встречалось в работах итальянского математика Тартальи ( около 1500 - 1557 гг. ) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.
В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори, а также в работах Ньютона. Учащиеся могут рассказать несколько фактов из биографии Ньютона.
Большой вклад в изучение дифференциального исчисления внесли Лейбниц, Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.
Однако у создателей дифференциального исчисления возникли проблемы, связанные с тем, что точные определения таких основных понятий как предел, непрерывность, действительное число, отсутствовали, рассуждения содержали логические пробелы, а иногда были ошибочны.

Таким образом, "новая" математика не отвечала
стандартам строгости, привычным для ученых, воспитанных на
классических образцах греческих математиков. Гениальная
интуиция таких гигантов, как Ньютон, Лейбниц, Эйлер помогала им
избегать ошибок.
Характерны 2 высказывания, относящиеся к 18-му столетию.
Известный математик М. Ролль писал, что новая наука есть коллекция
гениальных ошибок. А великий французский мыслитель - Вольтер
заметил, что это исчисление представляет собой искусство вычислять и
точно измерять вещи, существование которых не может быть доказано.
Начальный период развития новых ветвей математики, связанных с
понятиями функции, бесконечно малых величин, пределов и производных,
был охарактеризован Марксом как "мистический".
Лозунгом многих математиков 17 века был:
"Двигайтесь вперед, и вера в правильность результатов к вам придет".

Поздравляем победителей!!!

Д/з:
а) стр. 167 №3(б, г), №5(3а), №7(3а,б)
б)творческое задание: составить кроссворд по теме: «Производная и ее применение»