Содержание
- 2. Архитектурные сооружения г. Калачинска Калачинский историко-краеведческий музей. Омская область, г. Калачинск, ул. Ленина, д. 39.
- 3. Покрова Пресвятой Богородицы. Калачинский район, ул. Советская 1.
- 4. Приход православной церкви Воскресения Христова. г. Калачинск, ул. Октябрская, 8.
- 5. Театр кукол «Сказка». Г. Калачинск, ул. Калинина 3.
- 6. Верхняя и нижняя ставни окон Историка-краеведческого музея украшены резным узором . Если через центр рисунка провести
- 7. Тела обычно считают равными, те, которые совершенно одинаковы, или, точнее, которые при взаимном наложении совмещаются друг
- 8. Переносы — это перемещения вдоль прямой АВ на расстояние а. Такая операция применима лишь для объектов,
- 9. Нульмерная симметрия, как уже говорилось, присуща телам, бесконечно це вытянутым ни в одном особенном направлении. Очевидно,
- 10. Симметрия в химии. Симметрия в химии проявляется в геометрической конфигурации молекул, что сказывается на специфике физических
- 11. Симметрия в физике. Симметрия – одно из фундаментальных понятий в современной физике, играющее важнейшую роль в
- 12. Симметрия в литературе. Замечательным примером использования симметрии является человеческая деятельность, а именно – творческая – это
- 14. Скачать презентацию
Слайд 2
Архитектурные сооружения г. Калачинска Калачинский историко-краеведческий музей.
Омская область, г. Калачинск, ул.
Архитектурные сооружения г. Калачинска Калачинский историко-краеведческий музей. Омская область, г. Калачинск, ул.

Слайд 3Покрова Пресвятой Богородицы.
Калачинский район, ул. Советская 1.
Покрова Пресвятой Богородицы.
Калачинский район, ул. Советская 1.

Слайд 4Приход православной церкви Воскресения Христова.
г. Калачинск, ул. Октябрская, 8.
Приход православной церкви Воскресения Христова.
г. Калачинск, ул. Октябрская, 8.

Слайд 5Театр кукол «Сказка».
Г. Калачинск, ул. Калинина 3.
Театр кукол «Сказка».
Г. Калачинск, ул. Калинина 3.

Слайд 6Верхняя и нижняя ставни окон Историка-краеведческого музея украшены резным узором . Если
Верхняя и нижняя ставни окон Историка-краеведческого музея украшены резным узором . Если

Слайд 7Тела обычно считают равными, те, которые совершенно одинаковы, или, точнее, которые при
Тела обычно считают равными, те, которые совершенно одинаковы, или, точнее, которые при

Но наличия одних равных частей в фигуре еще недостаточно, чтобы признать фигуру симметричной: на рисунке 1, г лепестки венчика цветка расположены хаотично, незакономерно и фигура несимметрична, внизу (д) лепестки расположены однообразно, закономерно и венчик симметричен. Такое закономерное, однообразное расположение равных частей фигуры относительно друг друга и называют симметрией. Пары лепестков: а — совместимо равные; б — зеркально равные; в — и совместимо и зеркально равные. Фигуры из пяти лепестков: г — расположенных относительно друг друга хаотично; д — закономерно. Верхняя фигура асимметричная, нижняя — симметричная.
Слайд 8Переносы — это перемещения вдоль прямой АВ на расстояние а. Такая операция
Переносы — это перемещения вдоль прямой АВ на расстояние а. Такая операция

Аксиальная симметрия: а — медуза аурелия инсулинда; б — детская вертушка; в — молекула химического соединения. При повороте этих фигур на 360о равные части фигур совпадут друг с другом соответственно 4, 4, 6 раз.
Слайд 9Нульмерная симметрия, как уже говорилось, присуща телам, бесконечно це вытянутым ни в
Нульмерная симметрия, как уже говорилось, присуща телам, бесконечно це вытянутым ни в

Двусторонняя, или билатеральная, симметрия. Через середины фигур — рака, бабочки, листа растения — проходит плоскость симметрии, делящая каждую из фигур на две зеркальные половины.
Слайд 10Симметрия в химии.
Симметрия в химии проявляется в геометрической конфигурации молекул, что сказывается
Симметрия в химии.
Симметрия в химии проявляется в геометрической конфигурации молекул, что сказывается

Большинство простых молекул обладает элементами пространственной симметрии равновесной конфигурации: осями симметрии, плоскостями симметрии и т. д. Так, молекула аммиака NH3 обладает симметрией правильной треугольной пирамиды, молекула метана CH4 - симметрией тетраэдра. У сложных молекул симметрия равновесной конфигурации в целом, как правило, отсутствует, однако приближённо сохраняется симметрия отдельных её фрагментов (локальная симметрия). Наиболее полное описание симметрии как равновесных, так и неравновесных конфигураций молекул достигается на основе представлений о т. н. динамических группах симметрии - группах, включающих не только операции пространственной симметрии ядерной конфигурации, но и операции перестановки тождественных ядер в различных конфигурациях. Например, динамическая группа симметрии для молекулы NH3 включает также и операцию инверсии этой молекулы: переход атома N с одной стороны плоскости, образованной атомами Н, на другую её сторону.
Слайд 11Симметрия в физике.
Симметрия – одно из фундаментальных понятий в современной физике, играющее
Симметрия в физике.
Симметрия – одно из фундаментальных понятий в современной физике, играющее

В теоретической физике поведение физической системы описывается обычно некоторыми уравнениями. Если эти уравнения обладают какими-либо симметриями, то часто удаётся упростить их решение путём нахождения сохраняющихся величин. Например, следует, что инвариантность (неизменность) уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве – к закону сохранения импульса; инвариантность относительно вращений – к закону сохранения момента импульса.
Слайд 12Симметрия в литературе.
Замечательным примером использования симметрии является человеческая деятельность, а именно
Симметрия в литературе.
Замечательным примером использования симметрии является человеческая деятельность, а именно

В «Евгении Онегине» А.С. Пушкина мы наблюдаем симметрию положений: «Онегин, отвергнувший когда-то любовь Татьяны, сам через несколько лет вынужден испытывать горечь отвергнутой любви».
В трагедии А.С. Пушкина «Борис Годунов» прекрасно выписана симметрия образов. Убийцу царственного наследника, занявшего престол, сменяет на троне такой же умный, такой же наглый и беспощадный убийца юноши-царевича.
Рассмотрим буквы русского языка с точки зрения симметрии:
Назовите ось симметрии.
А; Д; Л; М; П; Е; Ф; Ш. (вертикальная ось симметрии) В; Е; З; К; С; Э; Ю. (горизонтальная ось симметрии) Ж; Н; О; Х. (и вертикальные и горизонтальные оси симметрии) Б; Г; И; Й; Р; У; Ц; Ч; Щ; Я. (ни вертикальные, ни горизонтальные оси)
В русском языке есть «симметричные» слова – палиндромы, которые можно читать одинаково в двух направлениях:
Шалаш, казак, радар, Алла, Анна, кок, поп, топот
Могут быть палиндромическими и предложения. Написаны тысячи таких предложений.
А роза упала на лапу Азора. (А. Фет) Я иду с мечем судия. (Т. Державин)
 Межнациональные отношения
Межнациональные отношения Тест по теме: трудовой договор
Тест по теме: трудовой договор Преподаватель физкультуры: Киселева Светлана Викторовна МОУ СОШ 9.
Преподаватель физкультуры: Киселева Светлана Викторовна МОУ СОШ 9. Приемы компрессии текста
Приемы компрессии текста  Декоративные георгины
Декоративные георгины «Разработка и апробация моделей центров сертификации профессиональных квалификаций и экспертно-методического центра в отрасли м
«Разработка и апробация моделей центров сертификации профессиональных квалификаций и экспертно-методического центра в отрасли м Значение лесов
Значение лесов Презентация+_Локально_нормативные+акты+организации_
Презентация+_Локально_нормативные+акты+организации_ Электронные таблицы 10 класс
Электронные таблицы 10 класс Статья 5. Никто не должен подвергаться пыткам или жестоким, бесчеловечным или унижающим достоинство обращению и наказанию
Статья 5. Никто не должен подвергаться пыткам или жестоким, бесчеловечным или унижающим достоинство обращению и наказанию Система экономиина масштабах для участников IT-кластера в Ярославской области
Система экономиина масштабах для участников IT-кластера в Ярославской области Народное музыкальное творчество
Народное музыкальное творчество Пионеры – герои во время Великой Отечественной войне
Пионеры – герои во время Великой Отечественной войне Реализация технологии деятельностного подхода на уроках в начальной школе
Реализация технологии деятельностного подхода на уроках в начальной школе Эксклюзив C&W
Эксклюзив C&W Модуль 4Сущность и формы познания
Модуль 4Сущность и формы познания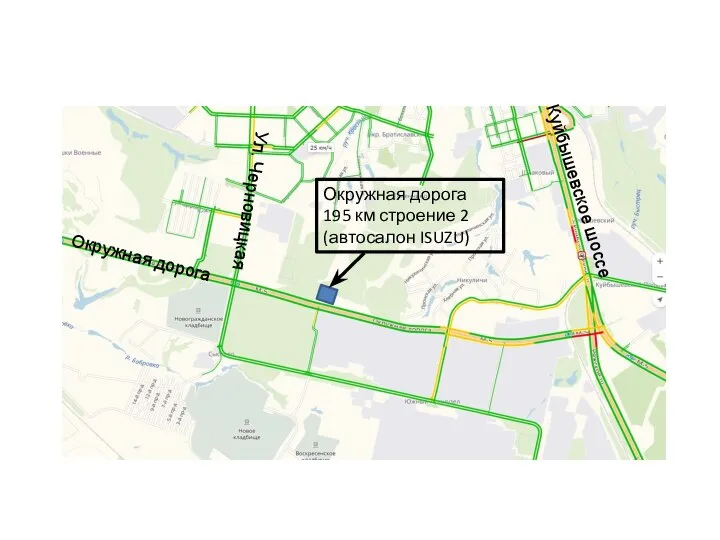 Окружная дорога 195 км строение 2 (автосалон ISUZU)
Окружная дорога 195 км строение 2 (автосалон ISUZU) Как создать эффективную схему работы финансовой службы и построить правильную систему мотивации
Как создать эффективную схему работы финансовой службы и построить правильную систему мотивации Кадровое бюро «охота»
Кадровое бюро «охота» Кабінет
Кабінет Фильтра Bosch
Фильтра Bosch Возрастные этапы становления социально-профессионального самоопределения
Возрастные этапы становления социально-профессионального самоопределения Мягконабивная игрушка Домовой
Мягконабивная игрушка Домовой Безлесные зоны юга России
Безлесные зоны юга России АДАПТАЦИЯ ПРИНЦИПОВ РЕГУЛИРОВАНИЯ К СОВРЕМЕННЫМ ЭКОНОМИЧЕСКИМ УСЛОВИЯМ
АДАПТАЦИЯ ПРИНЦИПОВ РЕГУЛИРОВАНИЯ К СОВРЕМЕННЫМ ЭКОНОМИЧЕСКИМ УСЛОВИЯМ Поклонение
Поклонение Принципи, шляхи й засоби адаптації європейської системи вищої освіти у вищу освіту України
Принципи, шляхи й засоби адаптації європейської системи вищої освіти у вищу освіту України Субъективная сторона преступления
Субъективная сторона преступления