Содержание
- 2. ПОНЯТИЕ ЛОГИЧЕСКОГО ЭЛЕМЕНТА. Логические элементы электронных схем. Синтез схем простых цифровых устройств.
- 3. Логическая функция - это функция логических переменных, которая может принимать только два значения : 0 или
- 4. Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными,
- 5. Бинарные операции (16шт, интересны 10) Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B) 2И "1" тогда и
- 6. Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера) Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса) "1" тогда
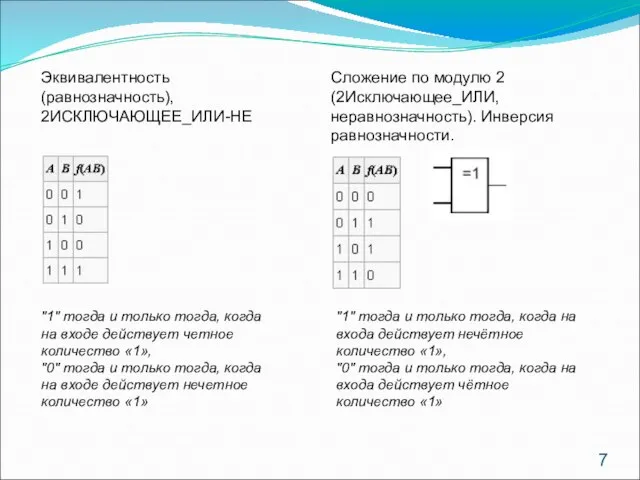
- 7. Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности. "1" тогда и только тогда,
- 8. Импликация от A к B (инверсия декремента) Импликация от B к A (инверсия инкремента) "0" тогда
- 9. Декремент. Запрет импликации по B. Инверсия импликации от A к B Инкремент. Запрет импликации по A.
- 10. Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции.
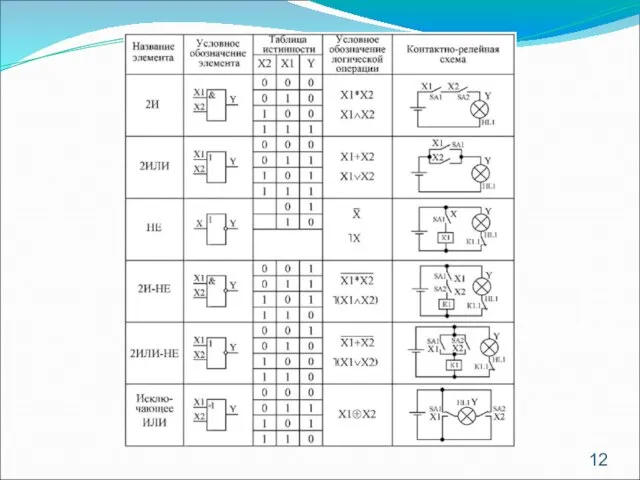
- 11. Физические реализации логических элементов Физические реализации одной и той же логической функции в разных системах электронных
- 13. Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию. Логическими элементами
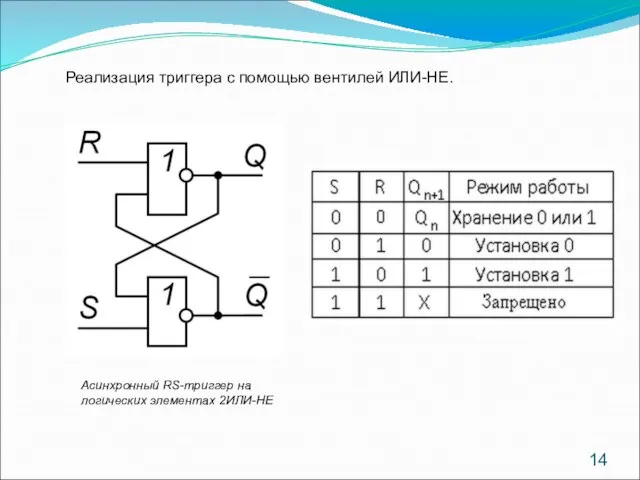
- 14. Реализация триггера с помощью вентилей ИЛИ-НЕ. Асинхронный RS-триггер на логических элементах 2ИЛИ-НЕ
- 15. Асинхронный триггер изменяет своё состояние непосредственно в момент появления соответствующего информационного сигнала(ов), с некоторой задержкой равной
- 16. Одноступенчатые триггеры состоят из одной ступени представляющей собой элемент памяти и схему управления, делятся на триггеры
- 17. Шифратор – это комбинационное устройство, преобразующее десятичные числа в двоичную систему счисления, причем каждому входу может
- 18. Дешифратором называется комбинационное устройство, преобразующее n-разрядный двоичный код в логический сигнал, появляющийся на том выходе, десятичный
- 19. Мультиплексором называют комбинационное устройство, обеспечивающее передачу в желаемом порядке цифровой информации, поступающей по нескольким входам на
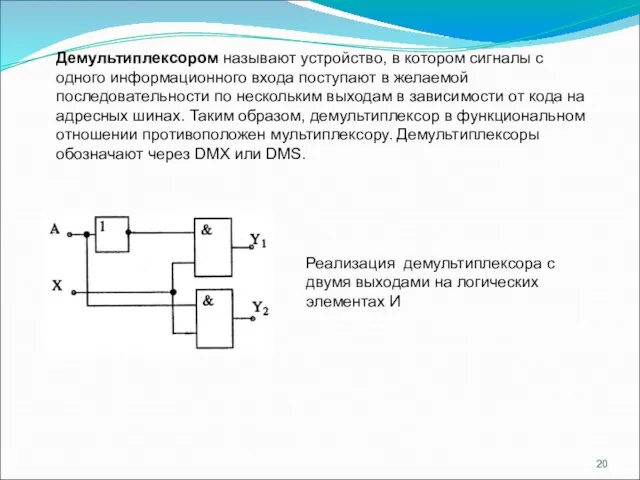
- 20. Демультиплексором называют устройство, в котором сигналы с одного информационного входа поступают в желаемой последовательности по нескольким
- 22. Скачать презентацию















 Декларирование товаров
Декларирование товаров CRAZY ENGLISH
CRAZY ENGLISH  Налоговый контроль. (Лекция 4)
Налоговый контроль. (Лекция 4) Доступ к среде передачи
Доступ к среде передачи Овердрафт
Овердрафт Представление инвестиционной группы QBF (часть 1)
Представление инвестиционной группы QBF (часть 1) Исследовательская работа школьников
Исследовательская работа школьников  Презентация на тему Спряжение глаголов
Презентация на тему Спряжение глаголов Внешняя политика Александра III
Внешняя политика Александра III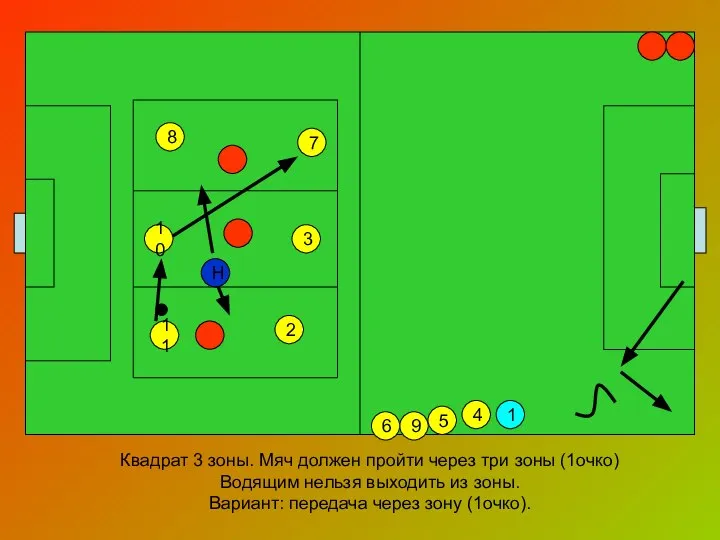 2 действия атакующих полузащитников 1-4-3-3
2 действия атакующих полузащитников 1-4-3-3 Спутниковая автоматизированная система мониторинга, охраны, диспетчерского управления транспортными средствами и стационарными
Спутниковая автоматизированная система мониторинга, охраны, диспетчерского управления транспортными средствами и стационарными КОНЦЕПЦИЯ ПРОВЕДЕНИЯ ПРАЗДНИКА «ДЕНЬ ГОРОДА 2007»
КОНЦЕПЦИЯ ПРОВЕДЕНИЯ ПРАЗДНИКА «ДЕНЬ ГОРОДА 2007» Научный руководитель О.Н.Сметанина Выполнила маг-ка гр.КАИД-511 Ахиярова Л.Н.
Научный руководитель О.Н.Сметанина Выполнила маг-ка гр.КАИД-511 Ахиярова Л.Н. Ошибки восприятия в деловом общении
Ошибки восприятия в деловом общении О признании иностранных (российских) дипломов в Латинской Америке
О признании иностранных (российских) дипломов в Латинской Америке Индивидуальная рефлексия Re*
Индивидуальная рефлексия Re* Презентация на тему Иван Сергеевич Тургенев «Вся моя биография в моих сочинениях»
Презентация на тему Иван Сергеевич Тургенев «Вся моя биография в моих сочинениях» Вопросы местного значения поселений в сфере жилищных отношений Закон № 131-ФЗ, ст. 14 (поселения), 16 (гор. округа): 1. К вопросам местно
Вопросы местного значения поселений в сфере жилищных отношений Закон № 131-ФЗ, ст. 14 (поселения), 16 (гор. округа): 1. К вопросам местно Кальцинированная сода
Кальцинированная сода Основные вопросы и задачи формирования электронного правительства в субъектах Российской Федерации
Основные вопросы и задачи формирования электронного правительства в субъектах Российской Федерации ggg
ggg ХЛЕБ-ВСЕМУ ГОЛОВА!
ХЛЕБ-ВСЕМУ ГОЛОВА! ДолгожителиМосквы
ДолгожителиМосквы проведение здоровьесберегающего урока
проведение здоровьесберегающего урока Взаимопревращение основных питательных веществ
Взаимопревращение основных питательных веществ  Московское предприятие. Требуется на постоянную работу
Московское предприятие. Требуется на постоянную работу Работаем с папой
Работаем с папой Российская автомобильная отрасль в условиях глобального экономического кризиса
Российская автомобильная отрасль в условиях глобального экономического кризиса