Содержание
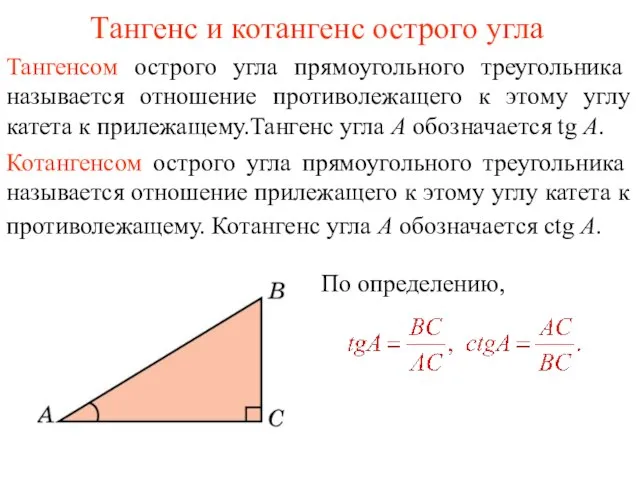
- 2. Тангенс и котангенс острого угла Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу
- 3. Тригонометрические функции Синус, косинус, тангенс и котангенс называют тригонометрическими функциями острого угла. Из определения тригонометрических функций
- 4. Вопрос 1 Что называется синусом острого угла прямоугольного треугольника? Ответ: Синусом острого угла прямоугольного треугольника называется
- 5. Вопрос 2 Как обозначается синус угла A? Ответ: Синус угла А обозначается sin A.
- 6. Вопрос 3 Что называется косинусом острого угла прямоугольного треугольника? Ответ: Косинусом острого угла прямоугольного треугольника называется
- 7. Вопрос 4 Как обозначается косинус угла A? Ответ: Косинус угла А обозначается cos A.
- 8. Вопрос 5 Что называется тангенсом острого угла прямоугольного треугольника? Ответ: Тангенсом острого угла прямоугольного треугольника называется
- 9. Вопрос 6 Как обозначается тангенс угла A? Ответ: Тангенс угла А обозначается tg A.
- 10. Вопрос 7 Что называется котангенсом острого угла прямоугольного треугольника? Ответ: Котангенсом острого угла прямоугольного треугольника называется
- 11. Вопрос 8 Как обозначается котангенс угла A? Ответ: Котангенс угла А обозначается ctg A.
- 12. Вопрос 9 Что называется тригонометрическими функциями острого угла? Ответ: Тригонометрическими функциями острого угла называются синус, косинус,
- 13. Вопрос 10 Чему равен катет, лежащий против угла в 30о? Ответ: Катет, лежащий против угла в
- 14. Упражнение 1 Найдите значения тригонометрических функций угла в 30о.
- 15. Упражнение 2 Найдите значения тригонометрических функций угла в 45о.
- 16. Упражнение 3 Найдите значения тригонометрических функций угла в 60о.
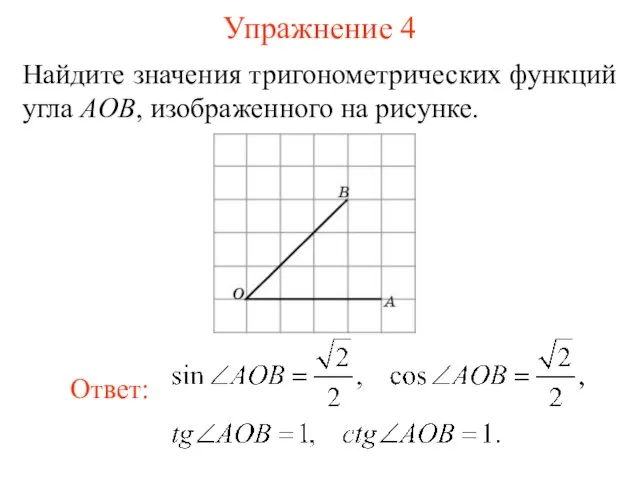
- 17. Упражнение 4 Найдите значения тригонометрических функций угла AOB, изображенного на рисунке.
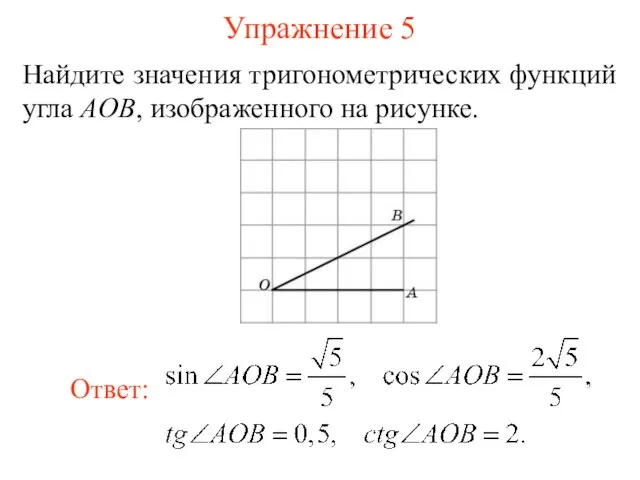
- 18. Упражнение 5 Найдите значения тригонометрических функций угла AOB, изображенного на рисунке.
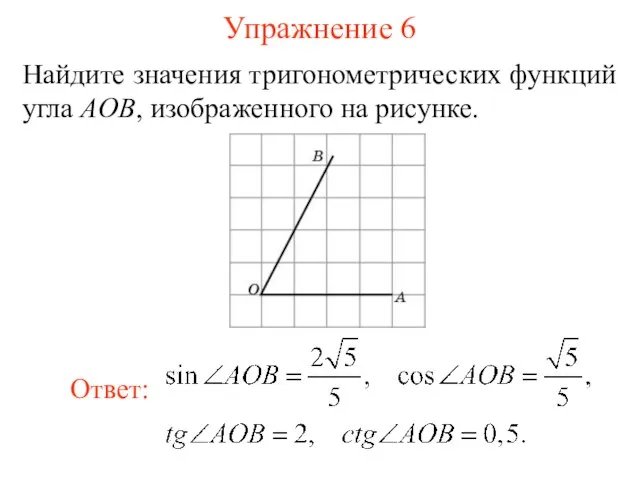
- 19. Упражнение 6 Найдите значения тригонометрических функций угла AOB, изображенного на рисунке.
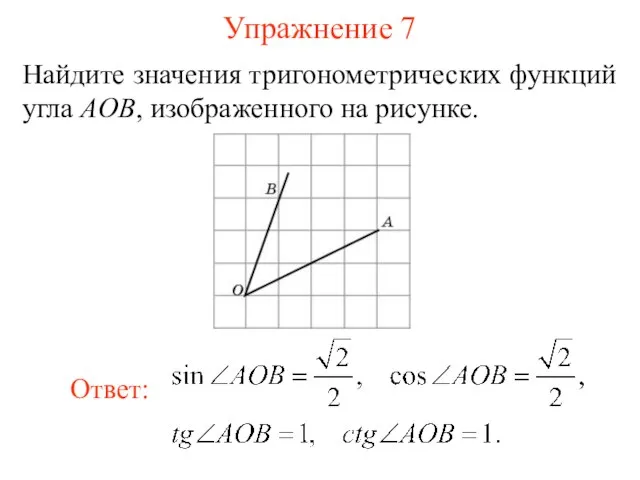
- 20. Упражнение 7 Найдите значения тригонометрических функций угла AOB, изображенного на рисунке.
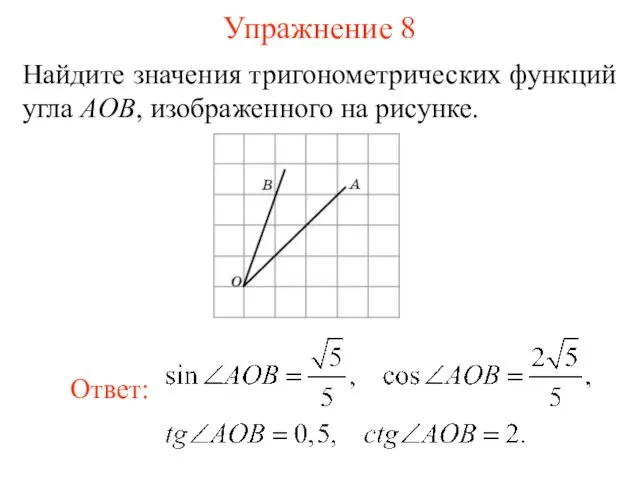
- 21. Упражнение 8 Найдите значения тригонометрических функций угла AOB, изображенного на рисунке.
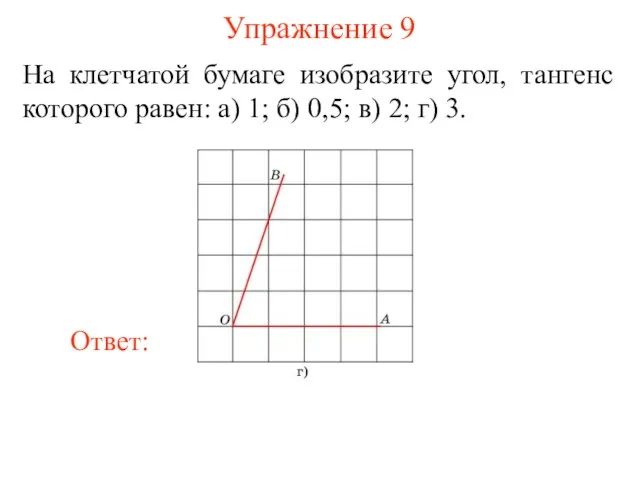
- 22. Упражнение 9 На клетчатой бумаге изобразите угол, тангенс которого равен: а) 1; б) 0,5; в) 2;
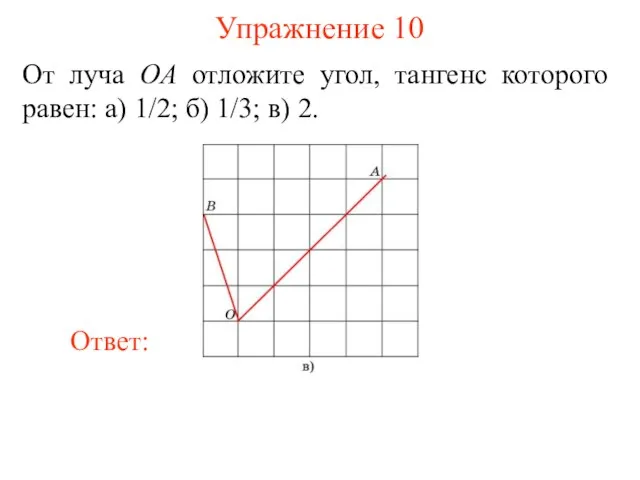
- 23. Упражнение 10 От луча OA отложите угол, тангенс которого равен: а) 1/2; б) 1/3; в) 2.
- 24. Упражнение 11 Может ли синус (косинус) угла быть равен ? Ответ: Нет, значения синуса и косинуса
- 25. Упражнение 12 Может ли тангенс (котангенс) угла быть равен ? Ответ: Да.
- 26. Упражнение 13 Катеты прямоугольного треугольника равны 12 см и 5 см. Найдите все тригонометрические функции его
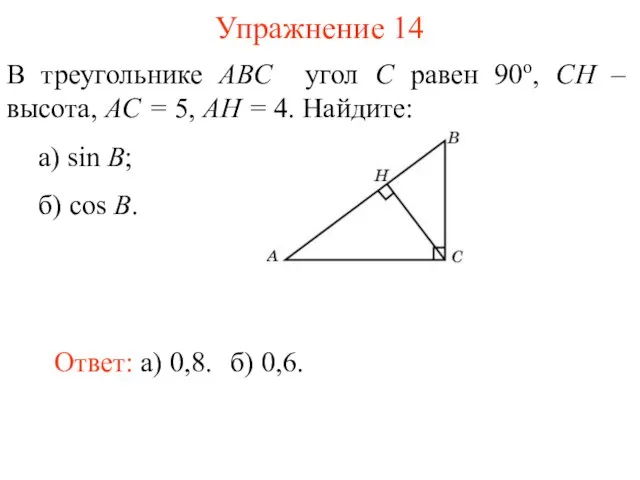
- 27. Упражнение 14 В треугольнике ABC угол C равен 90о, CH – высота, AC = 5, AH
- 28. Упражнение 15 В треугольнике ABC угол C равен 90о, CH – высота, BC = 5, BH
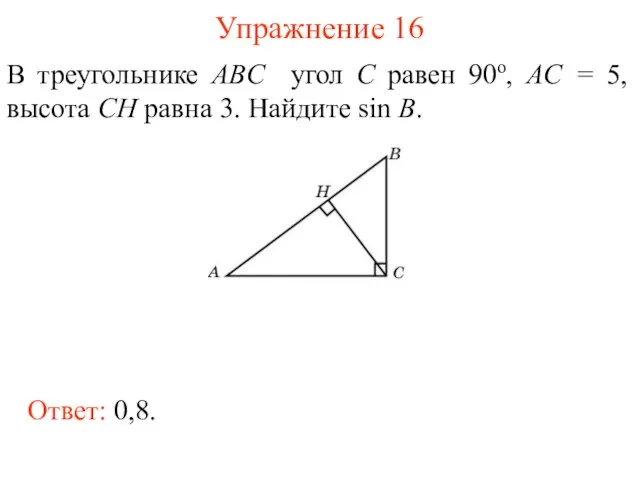
- 29. Упражнение 16 В треугольнике ABC угол C равен 90о, AC = 5, высота CH равна 3.
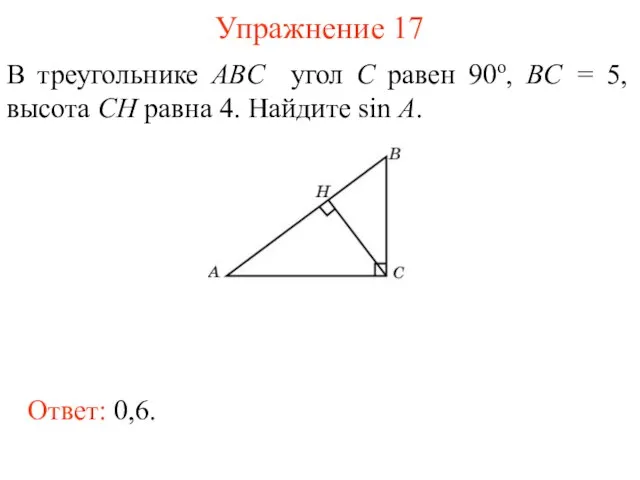
- 30. Упражнение 17 В треугольнике ABC угол C равен 90о, BC = 5, высота CH равна 4.
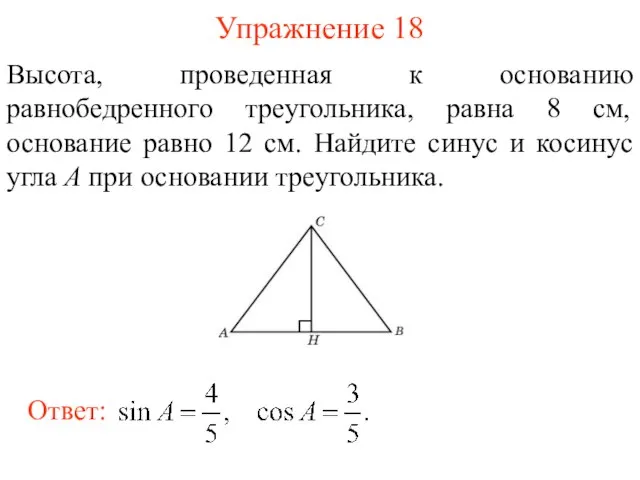
- 31. Упражнение 18 Высота, проведенная к основанию равнобедренного треугольника, равна 8 см, основание равно 12 см. Найдите
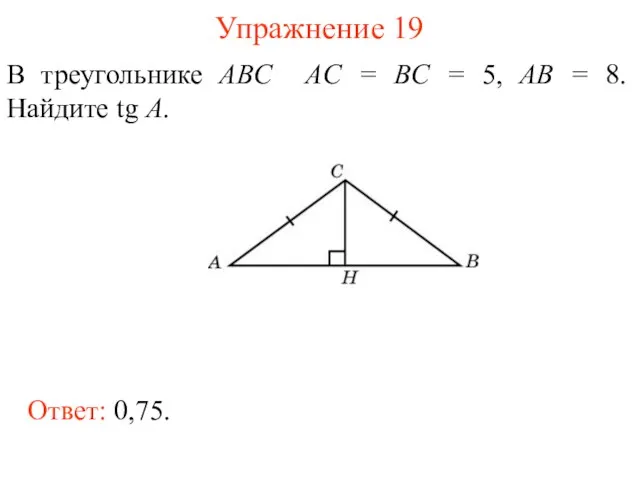
- 32. Упражнение 19 В треугольнике ABC AC = BC = 5, AB = 8. Найдите tg A.
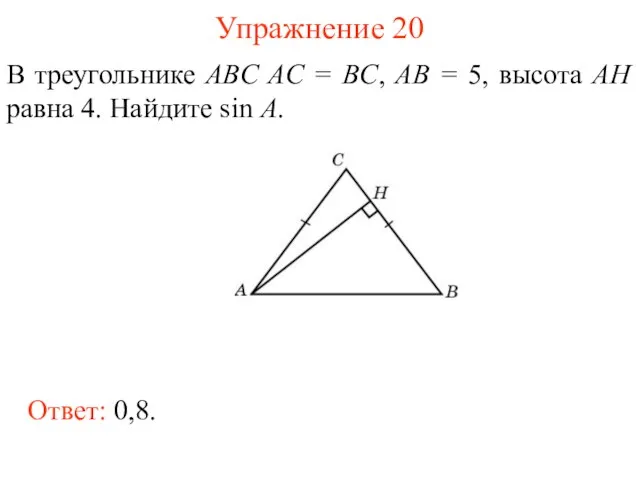
- 33. Упражнение 20 В треугольнике ABC AC = BC, AB = 5, высота AH равна 4. Найдите
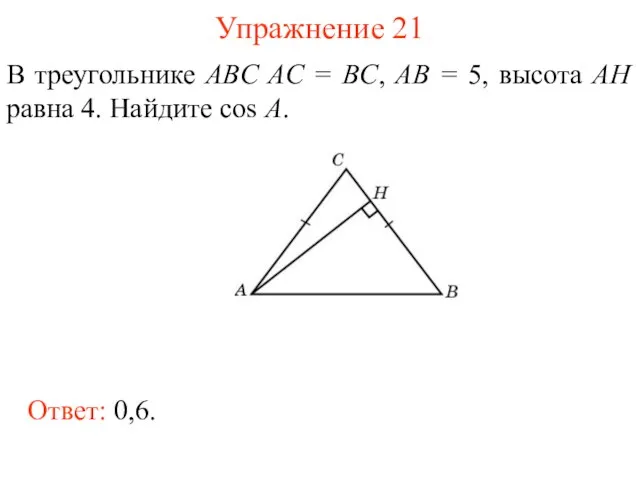
- 34. Упражнение 21 В треугольнике ABC AC = BC, AB = 5, высота AH равна 4. Найдите
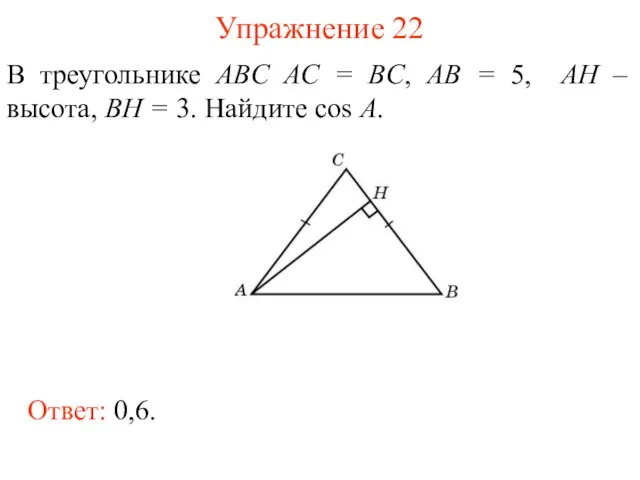
- 35. Упражнение 22 В треугольнике ABC AC = BC, AB = 5, AH – высота, BH =
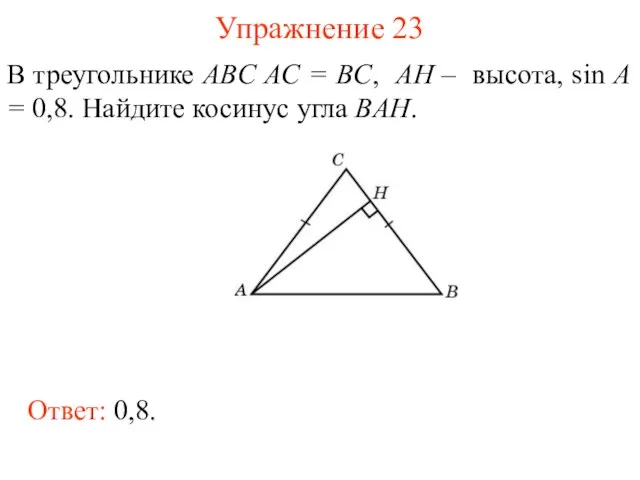
- 36. Упражнение 23 В треугольнике ABC AC = BC, AH – высота, sin A = 0,8. Найдите
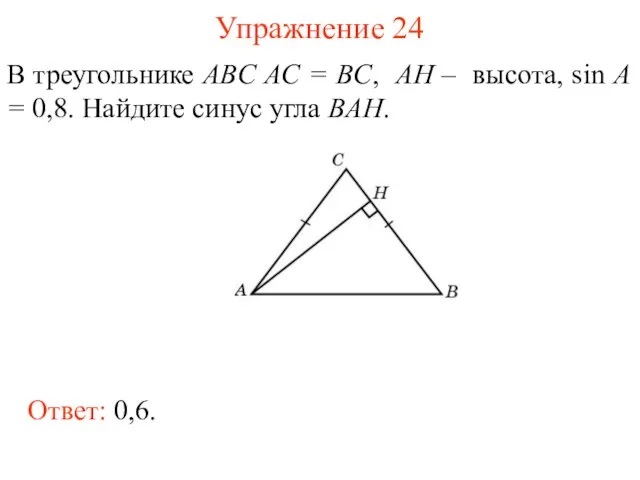
- 37. Упражнение 24 В треугольнике ABC AC = BC, AH – высота, sin A = 0,8. Найдите
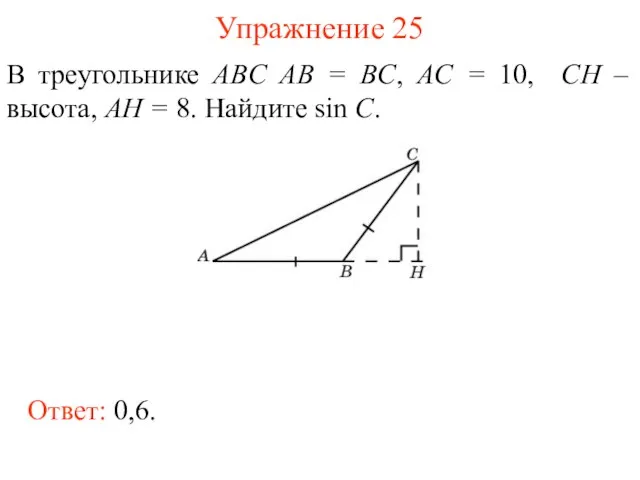
- 38. Упражнение 25 В треугольнике ABC AB = BC, AC = 10, CH – высота, AH =
- 39. Упражнение 26 В треугольнике ABC AB = BC, CH - высота, sin C = 0,4. Найдите
- 40. Упражнение 27* Найдите синус угла в 18о.
- 41. Упражнение 28* Найдите синус угла в 54о.
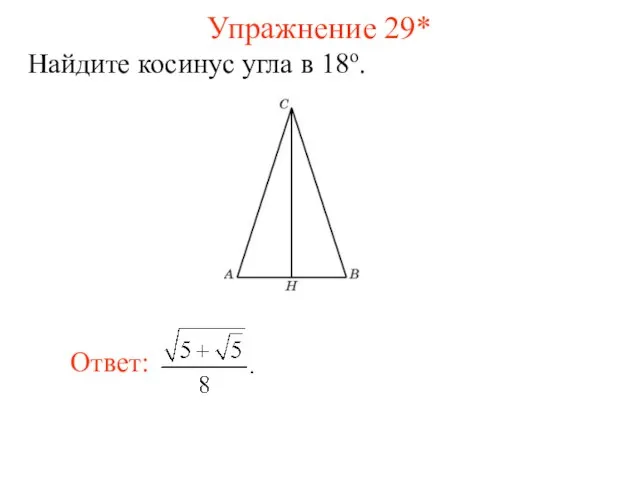
- 42. Упражнение 29* Найдите косинус угла в 18о.
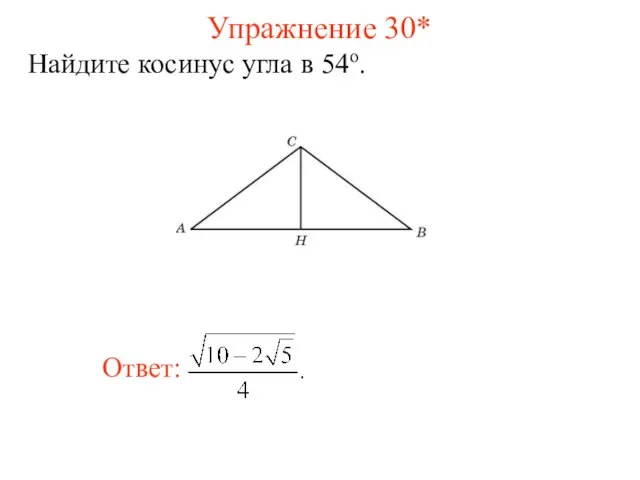
- 43. Упражнение 30* Найдите косинус угла в 54о.
- 44. Упражнение 31 Ответ: 37о. Мальчик прошел от дома по направлению на восток 800 м. Затем повернул
- 45. Упражнение 32 Ответ: 37о. Грибник, войдя в лес, в течение двух часов шел в направлении на
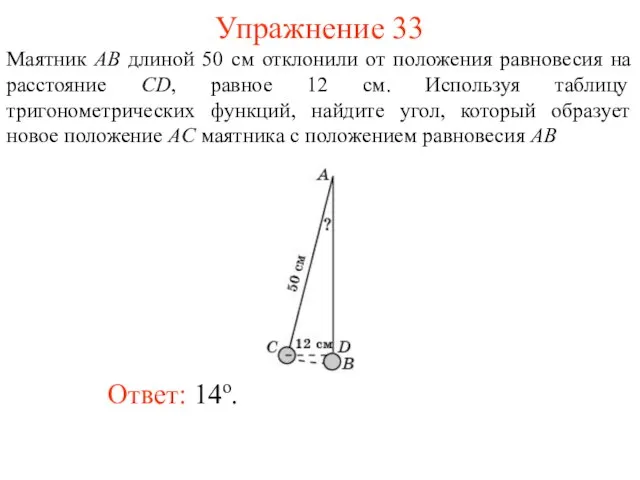
- 46. Упражнение 33 Ответ: 14о. Маятник AB длиной 50 см отклонили от положения равновесия на расстояние CD,
- 47. Упражнение 34 Ответ: 2о. Горная железная дорога поднимается на 1 м на каждые 30 м пути.
- 48. Упражнение 35 Ответ: 5о. Человек, пройдя вверх по склону холма 1000 м, поднялся на 90 м
- 49. Упражнение 36 Ответ: 2о. Использую таблицу тригонометрических функций, найдите приближенное значение угла, под которым виден столб
- 50. Упражнение 37 Ответ: 50о. Высота башни главного здания МГУ имени М.В. Ломоносова равна 240 м. Под
- 51. Упражнение 38 Ответ: 15о. Высота Останкинской телевизионной башни – 540 м. Используя таблицу тригонометрических функций, найдите
- 52. Упражнение 39 Ответ: 34о. Строение высоты 30 м бросает тень длиной 45 м. Используя таблицу тригонометрических
- 53. Упражнение 40 Ответ: 64о. Используя таблицу тригонометрических функций, найдите угол наклона солнечных лучей, если длина тени
- 54. Упражнение 41 Ответ: 31о. Лестница имеет ступеньки, ширина которых равна 30 см, а высота – 18
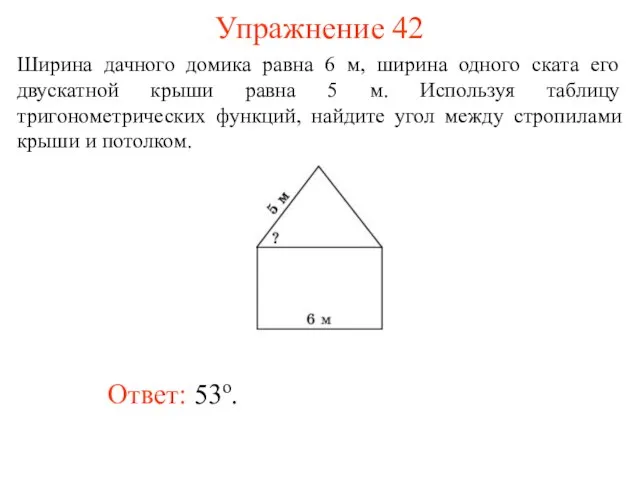
- 55. Упражнение 42 Ответ: 53о. Ширина дачного домика равна 6 м, ширина одного ската его двускатной крыши
- 56. Упражнение 43 Ответ: 37о. Ширина футбольных ворот равна 8 ярдам. Расстояние от 11-метровой отметки до линии
- 58. Скачать презентацию
































 Презентация на тему История герба России
Презентация на тему История герба России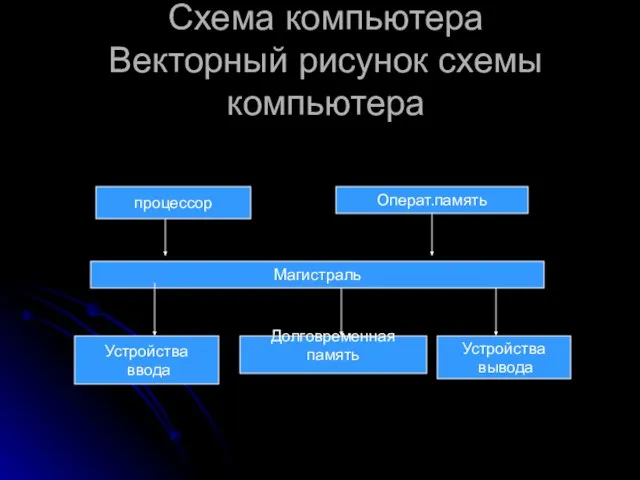 Схема компьютера Векторный рисунок схемы компьютера
Схема компьютера Векторный рисунок схемы компьютера История Масленицы
История Масленицы Президент Российской Федерации (функции и полномочия по Конституции РФ)
Президент Российской Федерации (функции и полномочия по Конституции РФ) www.seo.euvva.com
www.seo.euvva.com Роль отраслевой дипломатии в обеспечении энергетической безопасности
Роль отраслевой дипломатии в обеспечении энергетической безопасности Плотность
Плотность Воспитательная деятельность учителя
Воспитательная деятельность учителя Отработка навыков турпроектирования на основе ценностных ориентиров потребителей
Отработка навыков турпроектирования на основе ценностных ориентиров потребителей Проект «Здоровый образ жизни»
Проект «Здоровый образ жизни» Результаты исследования промо индустрии
Результаты исследования промо индустрии Новый год в открытках Алексея Исакова
Новый год в открытках Алексея Исакова КОКЛЮШ семинар Методические рекомендации по организации профилактических и противоэпидемических мероприятий по коклюшу
КОКЛЮШ семинар Методические рекомендации по организации профилактических и противоэпидемических мероприятий по коклюшу Языковые особенности в Квебеке
Языковые особенности в Квебеке ОРГАНИЗАЦИЯ ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИДЕТЕЙ СТАРШЕГО ДОШКОЛЬНОГО ВОЗРАСТА
ОРГАНИЗАЦИЯ ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИДЕТЕЙ СТАРШЕГО ДОШКОЛЬНОГО ВОЗРАСТА Подготовка к сочинению М. Ю. Лермонтов Мцыри
Подготовка к сочинению М. Ю. Лермонтов Мцыри Видеоадаптеры современных компьютеров
Видеоадаптеры современных компьютеров Планирование и исполнение расходов местных бюджетов РФ (на примере ЗАТО г. Островной Мурманской области)
Планирование и исполнение расходов местных бюджетов РФ (на примере ЗАТО г. Островной Мурманской области) Презентация на тему«Дельфы»
Презентация на тему«Дельфы» Громыко Алексей Олегович Компьютерное моделирование кинематики манипулятора промышленного робота Руководитель: доктор физ.-м
Громыко Алексей Олегович Компьютерное моделирование кинематики манипулятора промышленного робота Руководитель: доктор физ.-м Каша - пища наша
Каша - пища наша Понятие и признаки несостоятельности (банкротства)
Понятие и признаки несостоятельности (банкротства) Развитие угольной промышленности Красноярского края в контексте межрегиональной интеграции
Развитие угольной промышленности Красноярского края в контексте межрегиональной интеграции Фабрика санитарно-гигиенических изделийКрупнейший производитель бумажной санитарно-гигиенической продукции в УкраинеТМ «Неж
Фабрика санитарно-гигиенических изделийКрупнейший производитель бумажной санитарно-гигиенической продукции в УкраинеТМ «Неж Оформим буклет
Оформим буклет Уважаемые Дамы и Господа! Холдинг «Западно-Европейский Финансовый Союз» - динамично развивающаяся группа компаний, предоставляющ
Уважаемые Дамы и Господа! Холдинг «Западно-Европейский Финансовый Союз» - динамично развивающаяся группа компаний, предоставляющ Направление Контроля
Направление Контроля Radical Chic создал платки по мотивам картин Верещагина. Интернет-магазин Третьяковской галереи
Radical Chic создал платки по мотивам картин Верещагина. Интернет-магазин Третьяковской галереи