СИСТЕМЫ СЧИСЛЕНИЯ МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ

Вопросы и задания
1. Запишите десятичные эквиваленты следующих чисел:
а) 1728
б) 2ЕА16
в) 1010102
г) 10,12
д) 2436
2. Укажите, какое из чисел 1100112, 1114, 358 и 1В16 является:
а) наибольшим
б) наименьшим
3. Переведите целые числа из десятичной системы счисления в двоичную:
а) 89
б) 600
в) 2010

Вопросы и задания
4. Переведите целые числа из десятичной системы счисления в восьмеричную:
а) 513
б) 600
в) 2010
5. Переведите целые числа из десятичной системы счисления в шестнадцатеричную:
а) 513
б) 600
в) 2010

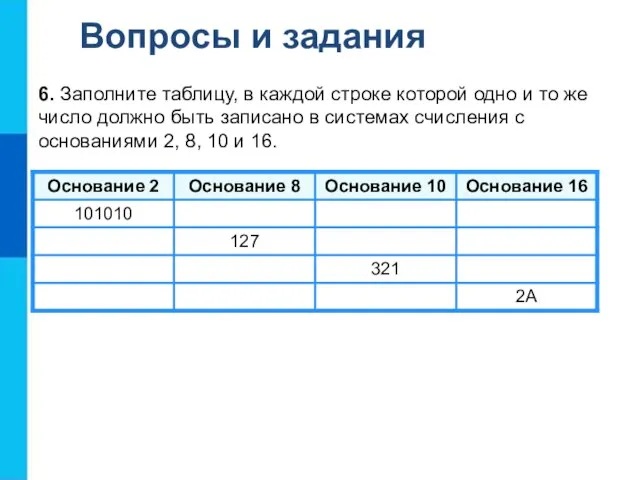
Вопросы и задания
6. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основаниями 2, 8, 10 и 16.

Двоичная арифметика
Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения:
02 + 02 = 02
02 + 12 = 12
12 + 02 = 12
12 + 12 = 102
или

Вопросы и задания
7. Выполните операцию сложения над двоичными числами:
а) 101010 + 1101
б) 1010 + 1010
в) 10101 + 111

Двоичная арифметика
Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения:
02 × 02 = 02
02 × 12 = 02
12 × 02 = 02
12 × 12 = 12
или

Вопросы и задания
8. Выполните операцию умножения над двоичными числами:
а) 1010 · 11
б) 111 · 101
в) 1010 · 111

Двоичная арифметика
Арифметика одноразрядных двоичных чисел
Арифметика многоразрядных двоичных чисел
Умножение и деление двоичных чисел

Вопросы и задания
9. Расставьте знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе:
а) 1100 ? 11 ? 100 = 100000;
б) 1100 ? 10 ? 10 = 100;
в) 1100 ? 11 ? 100 = 0.
10. Вычислите выражения:
а) (11111012 +AF16):368
б) 1258 + 1012 ·2A16 – 1418
Ответ дайте в десятичной системе счисления.

ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В КОМПЬЮТЕРЕ
МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ

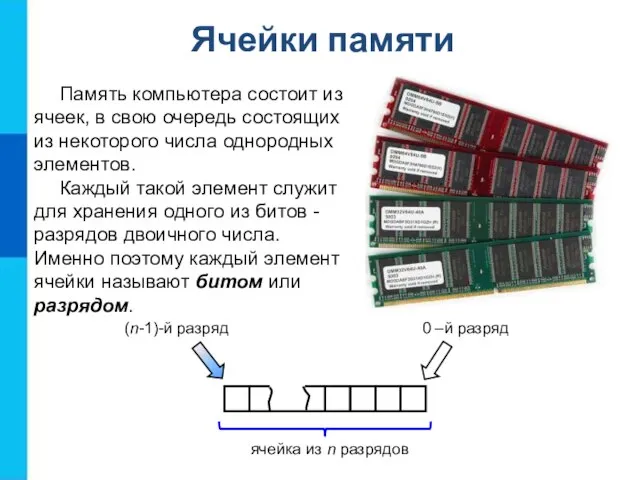
Ячейки памяти
Память компьютера состоит из ячеек, в свою очередь состоящих из некоторого числа однородных элементов.
Каждый такой элемент служит для хранения одного из битов - разрядов двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом.

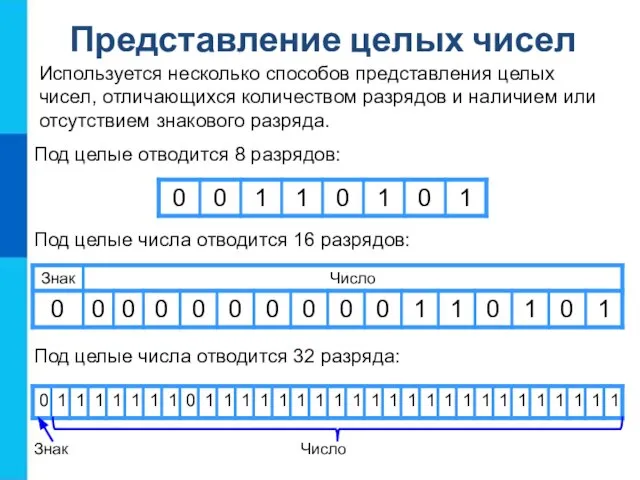
Используется несколько способов представления целых чисел, отличающихся количеством разрядов и наличием или отсутствием знакового разряда.
Представление целых чисел
Под целые отводится 8 разрядов:
Под целые числа отводится 16 разрядов:
Под целые числа отводится 32 разряда:
Знак
Число

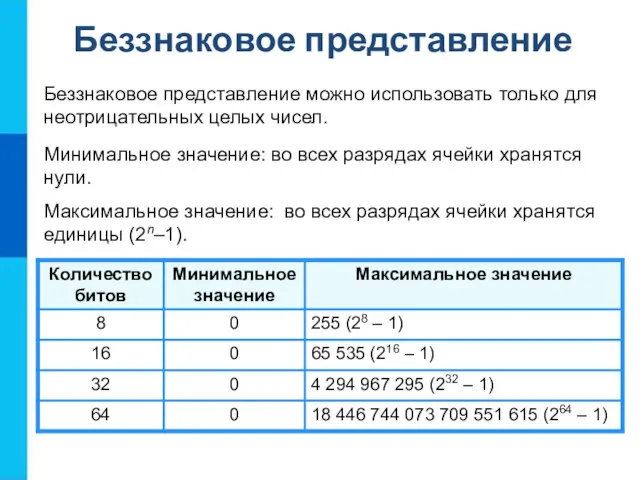
Минимальное значение: во всех разрядах ячейки хранятся нули.
Максимальное значение: во всех разрядах ячейки хранятся единицы (2n–1).
Беззнаковое представление можно использовать только для неотрицательных целых чисел.
Беззнаковое представление

Представление целого положительного числа в компьютере
число переводится в двоичную систему;
результат дополняется нулями слева в пределах выбранного формата;
Последний разряд слева является знаковым, в положительном числе он равен 0.

Представление целого положительного числа в компьютере
Например, положительное число 13510 в зависимости от формата представления в компьютере будет иметь следующий вид:
для формата в виде 1 байта – 10000111 (отсутствует знаковый разряд);
для формата в виде 2 байтов – 0 0000000 10000111;
для формата в виде 4 байтов –
0 0000000 00000000 00000000 10000111

Пример 1. Число 5310 = 1101012 в восьмиразрядном представлении имеет вид:
Число 53 в шестнадцатиразрядном представлении имеет вид:
Представление чисел в памяти компьютера

Представление со знаком
При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды - под само число.
Диапазон представления чисел - 2 n-1≤ x ≤ 2n-1-1,
где n - разрядность ячейки.
Минимальное значение: -2n-1.
Максимальное значение: 2n-1–1.
Если число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1.

Пример 2. Число 7310 = 10010012.
Прямой код числа 7310 в восьмиразрядном представлении имеет вид:
Прямой код
Прямой код числа -7310 в восьмиразрядном представлении имеет вид:
Прямой код используется главным образом для записи и выполнения операций с неотрицательными целыми числами. Для выполнения операций с отрицательными числами используется дополнительный код.

Представление целого отрицательного
числа в компьютере
число без знака переводится в двоичную систему;
результат дополняется нулями слева в пределах выбранного формата;
полученное число переводится в обратный код (нули заменяются единицами, а единицы – нулями);
к полученному коду прибавляется 1 (дополнительный код).

Представление целого отрицательного
числа в компьютере
Например, представим число -13510 в 2-байтовом формате:
13510 = 100001112 (перевод десятичного числа без знака в двоичный код);
0 0000000 10000111 (дополнение двоичного числа нулями слева в пределах формата);
0 0000000 10000111 → 1 1111111 01111000 (перевод в обратный код);
1 1111111 01111000 → 1 1111111 01111001 (перевод в дополнительный код).

Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды - под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1.

Задания
1. Представьте число 6310 в беззнаковом 8-разрядном формате.
2. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:
а) 01001100;
б) 00010101.
3. Какие из чисел 4438, 1010102, 25610 можно сохранить
в 8-разрядном формате?