Содержание
- 2. Совершенные числа Дружественные числа
- 3. На этой математической розе даны две темы: Совершенные числа и Дружественные числа. Для перехода необходимо нажать
- 4. Все мы говорим: «О, это совершенство», «Вы само совершенство» и т.п. Но что же значит слово
- 5. Содержание Определение История Свойства Факты
- 6. Определение Совершенное число́ (др.-греч. ἀριθμὸς τέλειος) — натуральное число, равное сумме всех своих собственных делителей (т.
- 7. Совершенное число 6 (1 + 2 + 3 = 6) 28 (1 + 2 + 4
- 8. История изучения Чётные совершенные числа Алгоритм построения чётных совершенных чисел описан в IX книге Начал Евклида,
- 9. История изучения Чётные совершенные числа Леонард Эйлер Начала Евклида
- 10. История изучения Чётные совершенные числа . Открытие. Первые четыре совершенных числа ? в Арифметике Никомаха Геразского
- 11. История изучения Чётные совершенные числа . Открытие. Региомонтан
- 12. История изучения Чётные совершенные числа . Открытие. В дальнейшем поиск затормозился вплоть до середины XX в.,
- 13. История изучения Нечётные совершенные числа До сих пор науке неизвестно ни одного нечётного совершенного числа. Но
- 14. Свойства совершенных чисел Все чётные совершенные числа (кроме 6) являются суммой кубов последовательных нечётных натуральных чисел:
- 15. Свойства совершенных чисел Сумма всех чисел, обратных делителям совершенного числа (включая его самого), равна 2. Все
- 16. Примечательные факты Совершенный характер чисел 6 и 28 был признан многими культурами, обратившими внимание на то,
- 17. В сочинении «Град Божий» Св. Августин высказал мысль о том, что хотя Бог мог сотворить мир
- 18. «Число 6 совершенно само по себе, а не потому, что Господь сотворил все сущее за 6
- 19. Дружественные числа С О Д Е Р Ж А Н И Е СОДЕРЖАНИЕ ОПРЕДЕЛЕНИЕ СПОСОБЫ НАХОЖДЕНИЯ
- 20. Листая энциклопедию, ища тему для проекта, мы наткнулись на «Дружественные числа». Нас заинтересовало, и мы решили
- 21. Дружественные числа Дружественные числа – два натуральных числа, для которых сумма всех делителей первого числа́ (кроме
- 22. Дружественные числа были открыты последователями Пифагора. Правда, пифагорейцы знали только одну пару дружественных чисел — 220
- 23. Формулу, дающую 3 пары дружественных чисел, открыл примерно в 850 году арабский астроном и математик Сабит
- 24. где n > 1 — натуральное число, а p, q, r— простые числа, то 2npq и
- 25. На ноябрь 2006 известно 11 446 960 пар дружественных чисел. Все они состоят из двух чётных
- 26. Способы нахождения Теорема Сабита Рецепт Вальтера Боро
- 27. Теорема Сабита Рецепт Вальтера Боро Если все три числа r = 9 · 22n - 1
- 28. Краткая таблица дружественных чисел 220 и 284 (Пифагор, около 500 до н. э.) 1184 и 1210
- 30. Скачать презентацию






















 Тема урока:Прикладная среда графического редактора Paint.
Тема урока:Прикладная среда графического редактора Paint. Презентация на тему Система национальных счетов
Презентация на тему Система национальных счетов Двадцатилетний брак великого князя Московского Василия III с Соломонией Сабуровой был бесплоден. Отправив законную жену в монастыр
Двадцатилетний брак великого князя Московского Василия III с Соломонией Сабуровой был бесплоден. Отправив законную жену в монастыр Cn(H2O)m
Cn(H2O)m 20140111_prezentatsiya_k_igre
20140111_prezentatsiya_k_igre Умей предупреждать болезни
Умей предупреждать болезни Еженедельное совещание. Статус работ блока Геология и разработка
Еженедельное совещание. Статус работ блока Геология и разработка Изделие Святой Николаус-Чудотворец
Изделие Святой Николаус-Чудотворец Среднее арифметическое, мода и размах ряда.
Среднее арифметическое, мода и размах ряда. Амплуа игроков в волейболе и их функции
Амплуа игроков в волейболе и их функции Страховые представители АО Страховая компания СОГАЗ-Мед
Страховые представители АО Страховая компания СОГАЗ-Мед «EVA 2011 Москва» 28 – 30 ноября 2011 Сбор и долговременное сохранение электронной информации в сфере культуры. Л.А. Куйбышев, Н.В. Браккер,
«EVA 2011 Москва» 28 – 30 ноября 2011 Сбор и долговременное сохранение электронной информации в сфере культуры. Л.А. Куйбышев, Н.В. Браккер,  Диего Веласкес. Сдача Бреды 1634–1635
Диего Веласкес. Сдача Бреды 1634–1635 К НЕМУ НЕ ЗАРАСТЕТНАРОДНАЯ ТРОПА А. С. Пушкину посвящается…
К НЕМУ НЕ ЗАРАСТЕТНАРОДНАЯ ТРОПА А. С. Пушкину посвящается… тема: «Воображение как общая способность»
тема: «Воображение как общая способность»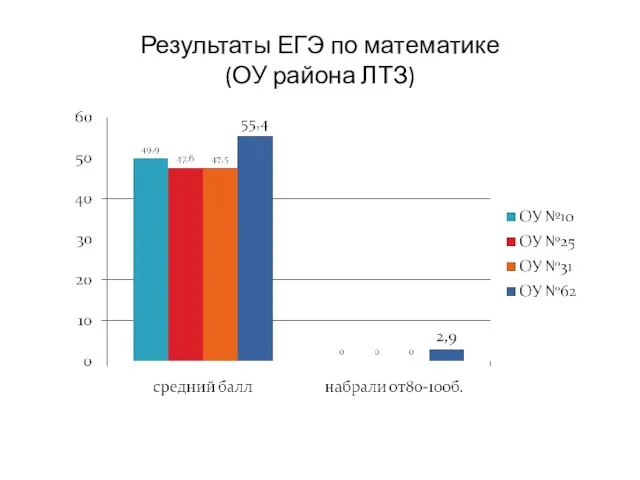 Результаты ЕГЭ по математике (ОУ района ЛТЗ)
Результаты ЕГЭ по математике (ОУ района ЛТЗ) Качество влияния личности на ход истории (на примере А. Гитлера и И. Сталина)
Качество влияния личности на ход истории (на примере А. Гитлера и И. Сталина) Организация обучения учителей по курсу «Основы религиозных культур и светской этики» в Калининградской области
Организация обучения учителей по курсу «Основы религиозных культур и светской этики» в Калининградской области ООО Глобал Контейнер Лоджистикс
ООО Глобал Контейнер Лоджистикс Жак Рене Ширак
Жак Рене Ширак Игра в слова
Игра в слова Бизнес-план Пончиковой
Бизнес-план Пончиковой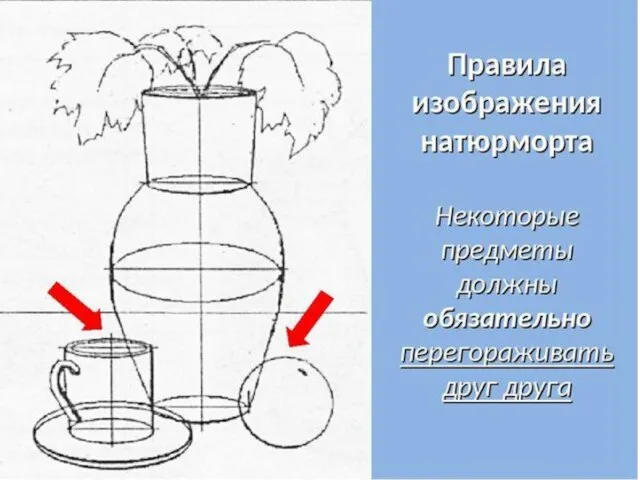 Занятие 3 года обучения на каникулах. Декоративный натюрморт
Занятие 3 года обучения на каникулах. Декоративный натюрморт Лабораторная группаРезультаты серологического этапа ДЭН выводы, задачи2008 год
Лабораторная группаРезультаты серологического этапа ДЭН выводы, задачи2008 год Виды наказаний
Виды наказаний Ультразвуковой датчик
Ультразвуковой датчик Легенды театральной сцены
Легенды театральной сцены ПОДПИСКА
ПОДПИСКА