Способы преобразования чертежа

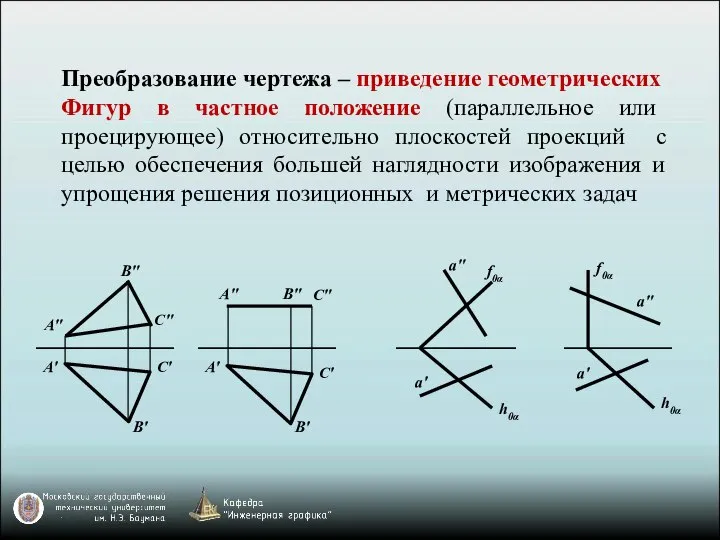
Преобразование чертежа – приведение геометрических
Фигур в частное положение (параллельное или проецирующее) относительно плоскостей проекций с целью обеспечения большей наглядности изображения и упрощения решения позиционных и метрических задач
A'
B'
C'
A'
B'
C'
a'
a'
B"
B"
A"
C"
C"
A"
a"
a"
h0α
h0α
f0α
f0α

Частные положения фигур относительно плоскостей проекций более удобны для решения геометрических задач: метрических задач (определение длины, угла, площади) и позиционных задач (определение положения геометрических фигур).
Два пути решения задачи изменения положения фигуры относительно плоскостей проекций:
изменить положение плоскостей проекций, не изменяя положения фигуры;
2) изменить положение фигуры, не меняя положения плоскостей проекций

Условия преобразования:
1). Положение фигуры неизменно;
2). Изменяется положение одной
из двух плоскостей проекций;
3). Новую плоскость проекций располагают
перпендикулярно оставшейся плоскости проекций;
4). Положение новой плоскости проекций может быть
задано или выбрано
Способ замены плоскостей проекций
Рис. 5.3

A"
B"
B'
A'
π2
π1
x
Ах
π1
π3
x1
Вх
Ах1
A"'
B"'
|AB|
α
Вх1
Преобразовать чертеж прямой общего положения в чертеж прямой уровня (рис. 5.5)
α = АВ^π1
Новая ось || одной из проекций отрезка
x1 || А'В'
Основные задачи,
решаемые заменой одной плоскости проекций
Рис. 5.5
zA
zB
zA
zB

A'
π2
π1
x
π1
π3
x1
A'"≡ B'"
B'
2. Преобразовать чертеж прямой уровня в чертеж проецирующей прямой (рис. 5.6)
Новая ось ┴ одноименной проекции линии уровня
x1 ⊥ h'
h"
B"
A"
h'
z
z
Рис. 5.6

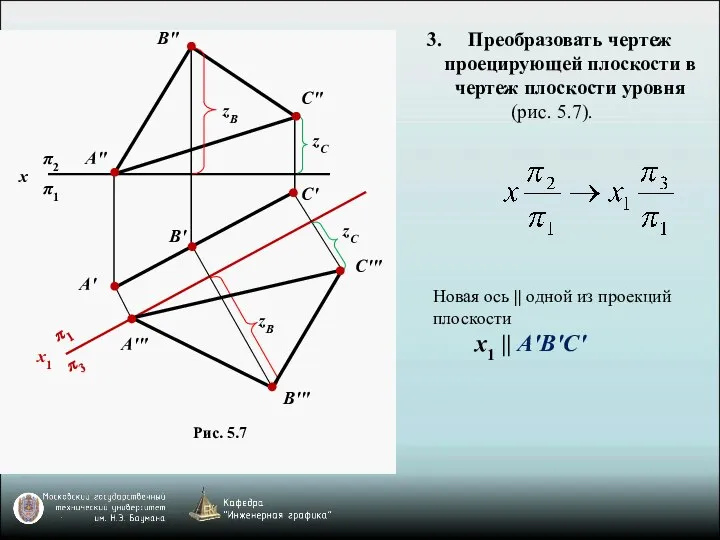
Преобразовать чертеж проецирующей плоскости в чертеж плоскости уровня
(рис. 5.7).
Рис. 5.7
x
π2
π1
A"
B"
C"
A'
B'
C'
A'"
B'"
C'"
zB
zC
zB
zC
x1
π3
π1
Новая ось || одной из проекций плоскости
x1 || А'В'C'

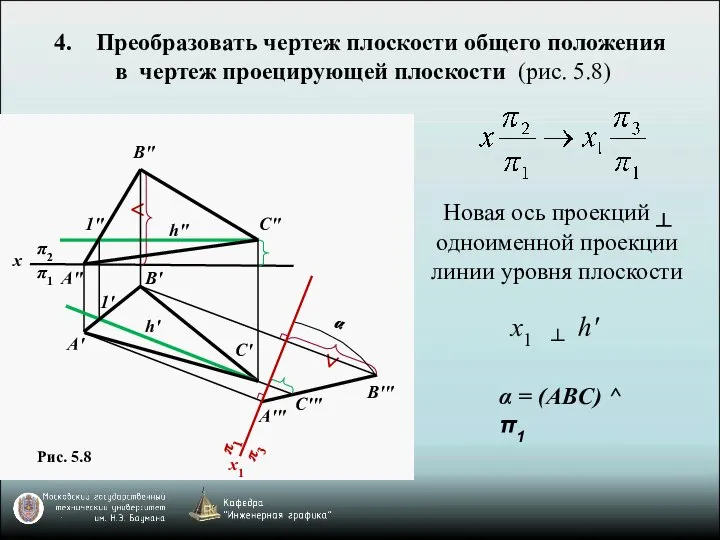
Рис.
Преобразовать чертеж плоскости общего положения
в чертеж проецирующей плоскости (рис. 5.8)
Новая ось проекций ┴
одноименной проекции линии уровня плоскости
x1
x
π2
π1
π1
π3
A'
C'
B'
B"
C"
A"
h"
1"
h'
1'
A'"
B'"
C'"
x1 ┴ h'
α
α = (ABC) ^ π1
Рис. 5.8

Основные задачи,
решаемые заменой двух плоскостей проекций
Преобразовать чертеж прямой общего положения в чертеж проецирующей прямой (рис. 5.9)
x1
x2
x
π2
π1
π1
π3
π3
π4
A'"
B'"
B'
A'
A"
B"
AIV≡ BIV
zA
zA
zB
zB
Рис. 5.9

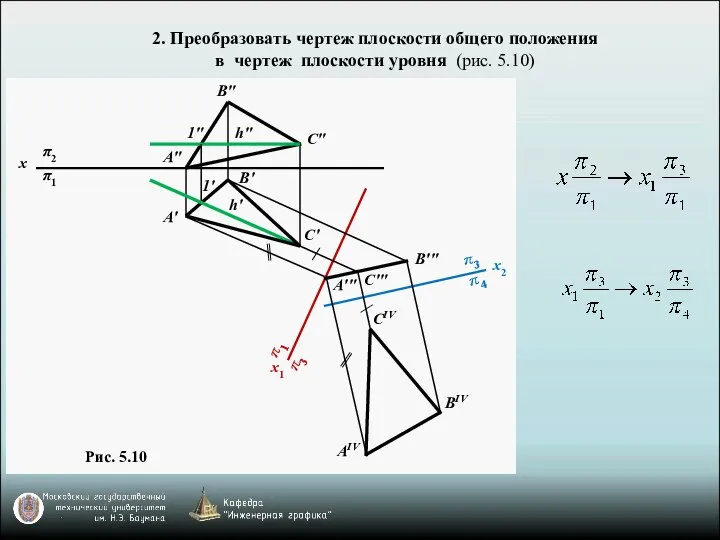
2. Преобразовать чертеж плоскости общего положения
в чертеж плоскости уровня (рис. 5.10)
π3
π2
π1
x
x1
x2
π4
π1
π3
C"
1"
A"
B"
h"
A'
C'
B'
h'
1'
C'"
B'"
A'"
AIV
BIV
CIV
║
║
/
/
Рис. 5.10

CПОСОБ ВРАЩЕНИЯ
Суть способа вращения – фигура переводится в частное положение относительно неизменной системы основных плоскостей проекций путем вращения вокруг некоторой оси.
Вращение – перемещение точки по окружности в плоскости, перпендикулярной оси вращения. Пересечение плоскости вращения с осью вращения – центр вращения. Расстояние от точки до центра вращения – радиус вращения
Алгоритм построения новой проекции точки A
Задать ось вращения i
Провести плоскость вращения α ┴ i
Найти центр вращения O = α ∩ i
Определить радиус вращения R = |AO|
Задать плоскость совмещения β
«Довернуть» вращаемую точку в положение A1
до совмещения с плоскостью β

СПОСОБ ВРАЩЕНИЯ ВОКРУГ ПРОЕЦИРУЮЩЕЙ ПРЯМОЙ
Рис. 5.11
Условия преобразования:
1. ось вращения i неподвижна и перпендикулярна плоскости проекций;
2. все точки фигуры перемещаются по окружностям, плоскости которых перпендикулярны оси i;
3. точки лежащие на оси вращения i неподвижны
β

Рис. 5.12
f0α
h0β
A1'
A2'
A'
≡ O'
A1"
A"
A2"
B"
i"
O"
Пример: Повернуть отрезок AB вокруг проецирующей прямой i
m'
m"
x
B'
≡ i'
|R|
|AB|
α

Вращение геометрической фигуры вокруг линии уровня производится с целью ее совмещения с плоскостью уровня.
Применяется этот способ в основном для преобразования плоскости общего положения в плоскость уровня при решении следующих задач:
1) определение величины плоской фигуры;
2) определение величины плоского угла;
3) построение в заданной плоскости какой-либо фигуры по заданным условиям.
Линия уровня, вокруг которой вращается плоскость общего положения, должна принадлежать этой плоскости. В этом случае вращение плоскости сводится к вращению только одной точки, не принадлежащей оси вращения.
СПОСОБ ВРАЩЕНИЯ ВОКРУГ ПРЯМОЙ УРОВНЯ

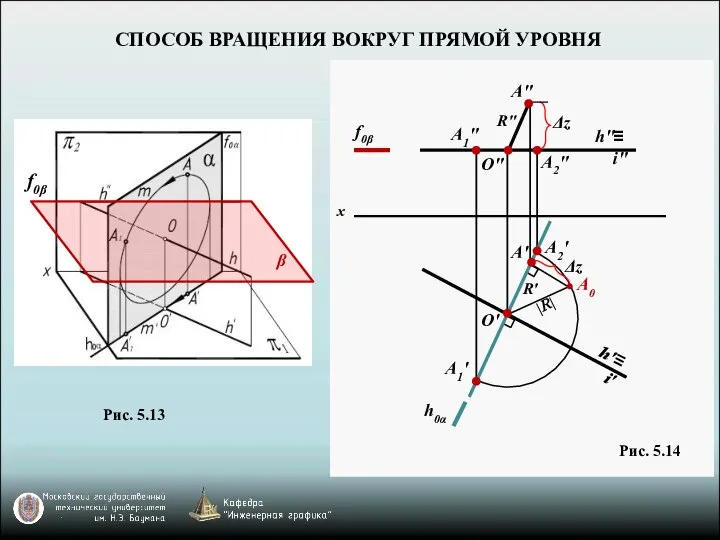
СПОСОБ ВРАЩЕНИЯ ВОКРУГ ПРЯМОЙ УРОВНЯ
Рис. 5.13
Рис. 5.14
β
f0β
h"
≡ i"
h'
≡ i'
f0β
h0α
A'
O'
R'
|R|
A1'
A2'
O"
A"
R"
A1"
A2"
A0
Δz
Δz
x