Содержание
- 2. Содержание разделов умножение на девять правила умножения разных чисел по Берману и Трахтенбергу возведение в квадрат
- 3. Цель работы: Облегчить и рационализировать вычисления; Обеспечить большую надежность вычисления.
- 4. Задачи: Изучить приемы быстрого счета по Трахтенбергу, Берману; Произвести исследования систем быстрого счета при умножении, выявить
- 5. Пальцевый счет Умножение однозначного числа на 9 на пальцах рук Это правило вывели в Древней Индии.
- 6. Рим (I век до н.э.) 10 х (а-5) + (в -5) +(10-а) х (10-в)=ав 5 5
- 7. УМНОЖЕНИЕ НА ОДИННАДЦАТЬ. (По Трахтенбергу) Последняя цифра множимого (число, которое умножается) записывается как самая правая цифра
- 8. Пример: 633 умножить на 11 Ответ пишется под 633, по одной цифре справа налево, как указано
- 9. 633 умножить на 11 Первое правило. Напишите последнюю цифру числа 633 в качестве правой цифры результата:
- 10. Второе правило. Каждая последующая цифра числа 633 складывается со своим правым соседом и записывается в результат.3+3
- 11. Применим правило еще раз: 6+3 будет 9. Записываем и эту цифру в результате: 633 х 11
- 12. Третье правило. Первая цифра числа 633, т.е. 6, становится левой цифрой результата: 633 х 11 6963
- 13. УМНОЖЕНИЕ НА ОДИННАДЦАТЬ (По Берману) Берман вывел, что при умножении на 11 число нужно умножить на
- 14. Пример: 110 х 11 110 х 11 = 110 х (10 + 1) = 110 х
- 15. ___ ___ ___ авс х 11 = авс х (10 + 1) = авс х 10
- 16. УМНОЖЕНИЕ НА ДВЕНАДЦАТЬ (По Трахтенбергу) Правило умножения на 12 : Нужно удваивать поочередно каждую цифру и
- 17. Пример: 63 247 х 12 Напишите цифры множимого через интервал и каждую цифру результата пишите точно
- 18. 063247 х 12 4 дважды 7 будет = 14, переносим 1 063247 х 12 64 дважды
- 19. 063247 х 12 964 дважды 2 плюс 4 плюс 1 будет = 9 Следующие шаги аналогичны.
- 20. УМНОЖЕНИЕ НА ДВЕНАДЦАТЬ. (По Берману) При умножении на 12 можно число умножить сначала на 6, а
- 21. Пример: 136 х 12 136 х 12 = 136 х 6 х 2 =816 х 2
- 22. Пример: 136 х 12 136 х 12 = 136 х 3 х 2 х 2 =
- 23. УМНОЖЕНИЕ НА ШЕСТЬ (По Трахтенбергу) Прибавить к каждой цифре половину «соседа» Пример: 0622084 х 6 0622084
- 24. Пример: 0622084 х 6 0622084 х 6 04 Вторая цифра 8, ее «сосед» 4. Мы берем
- 25. 0622084 х 6 504 Следующая цифра ноль. Мы прибавляем к ней половину «соседа» 8 (4), т.е.
- 26. Остальные шаги аналогичны. Окончательный ответ: 0622084 х 6 3732504
- 27. Правило умножения на 6 Является ли «сосед» четным или нечетным – никакой роли не играет. Мы
- 28. Пример: 0443052 х 6 0443052 х 6 2 2 – четная и не имеет «соседа», напишем
- 29. 0443052 х 6 312 Половина от 5 будет 2, и прибавим перенос (1), пишем 3. 0443052
- 30. 0443052 х 6 58312 4 + половина от 3(1), будет 5. 0443052 х 6 658312 4
- 31. 0443052 х 6 2658312 ноль + половина от 4(2), будет 2. Ответ: 2 658 312. Пример:
- 32. УМНОЖЕНИЕ НА ШЕСТЬ (По Берману) Умножить Число на шесть это все равно, что умножить на два
- 33. Пример: 18 х 6 18 х 2 х 3 = 36 х 3 = 108 Ответ:
- 34. Пример: 75 х 6 75 х 2 х 3 = 150 х 3 = 450 Ответ:
- 35. ВОЗВЕДЕНИЕ ДВУХЗНАЧНЫХ ЧИСЕЛ В КВАДРАТ (Берман, Трахтенберг) Нужно возвести в квадрат любое двухзначное число: Пример: 43=43х43=1849
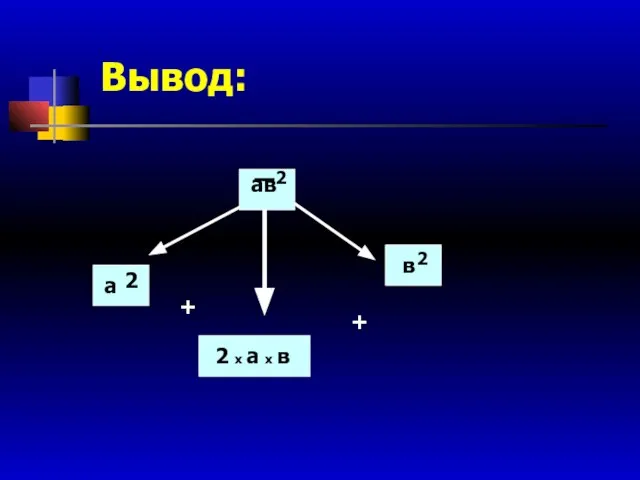
- 36. Вывод: ав 2 в 2 + 2 х а х в + а 2
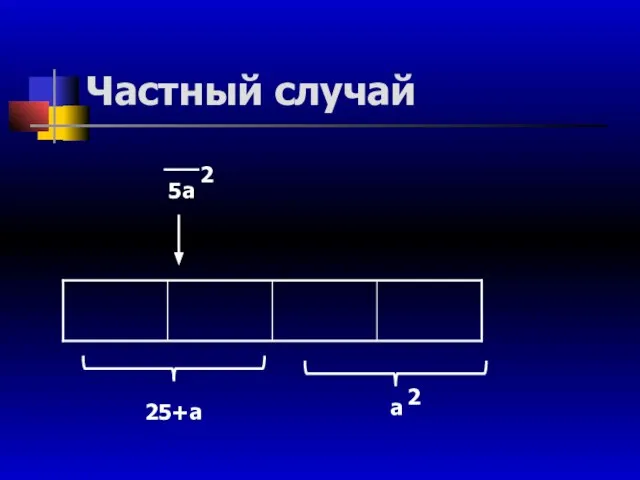
- 37. Частный случай 5а 2 25+а а 2
- 38. 53 2 56 2
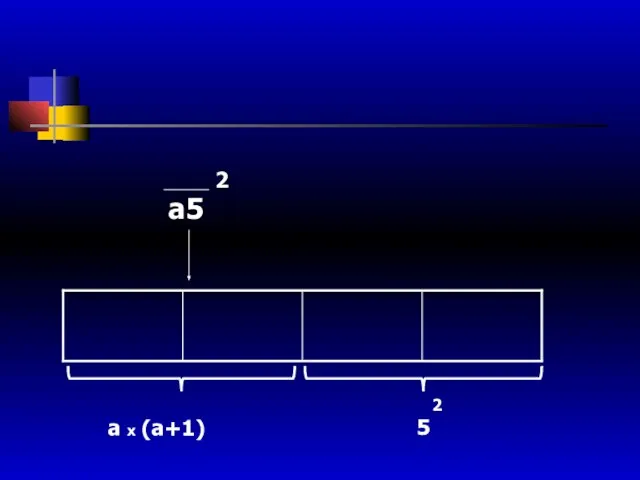
- 39. а5 2 а х (а+1) 5 2
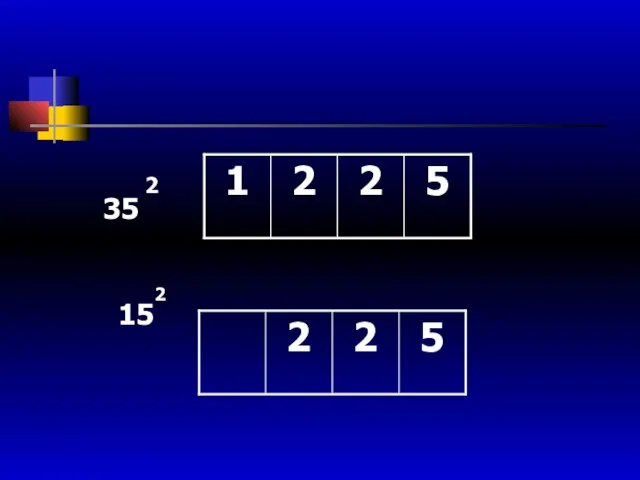
- 40. 35 2 15 2
- 41. 2 2 15=1х(1+1) 5х5=225 51=5х5+1 1х1=2601 2 2 25=2х(2+1) 5х5=625 52=5х5+2 2х2=2704 2 2 35=3х(3+1) 5х5=1225
- 42. 2 2 55=5х(5+1) 5х5=3025 55=5х5+5 5х5=3025 2 2 65=6х(6+1) 5х5=4225 56=5х5+6 6х6=3136 2 2 75=7х(7+1) 5х5=5625
- 43. УМНОЖЕНИЕ ТРЕХЗНАЧНОГО ЧИСЛА НА ТРЕХЗНАЧНОЕ (По Берману) х 512 625 х 512 625 + 300210 16.
- 44. УМНОЖЕНИЕ МНОГОЗНАЧНОГО ЧИСЛА НА МНОГОЗНАЧНОЕ (По Трахтенбергу) 37654 Х 498 301232 338886 150516 . 18751692 Используем
- 45. ЗАКЛЮЧЕНИЕ Система быстрого счета по Трахтенбергу основана на закономерностях умножения чисел. Чтобы умножить на 11, 12,
- 47. Скачать презентацию








































 Материалы для подготовки к контрольной работе по теме Греция
Материалы для подготовки к контрольной работе по теме Греция Управление человеческими ресурсами
Управление человеческими ресурсами Администрирование почтового сервера
Администрирование почтового сервера Загробная жизнь в Древнем Египте: гробницы и саркофаги.
Загробная жизнь в Древнем Египте: гробницы и саркофаги. Учимся письменному пересказу
Учимся письменному пересказу ОБЩЕСТВЕННАЯ ПАЛАТА ОМСКОЙ ОБЛАСТИ ОБЩЕСТВЕННЫЕ СЛУШАНИЯ «ОБ УСТАНОВКЕ ПАМЯТНИКА А.В. КОЛЧАКУ В г. ОМСКЕ» 19 июля 2012 года
ОБЩЕСТВЕННАЯ ПАЛАТА ОМСКОЙ ОБЛАСТИ ОБЩЕСТВЕННЫЕ СЛУШАНИЯ «ОБ УСТАНОВКЕ ПАМЯТНИКА А.В. КОЛЧАКУ В г. ОМСКЕ» 19 июля 2012 года  2.1.1. Содержание и последствия промышленного переворота для мировой экономики. 2.1.2. Англия – родина промышленной революции. 2.1.3. Кап
2.1.1. Содержание и последствия промышленного переворота для мировой экономики. 2.1.2. Англия – родина промышленной революции. 2.1.3. Кап Отношение к красоте человеческого тела как к великой ценности, данной природой, на протяжении многовековой истории человеческого
Отношение к красоте человеческого тела как к великой ценности, данной природой, на протяжении многовековой истории человеческого  Михаил Тариелович Лорис-Меликов
Михаил Тариелович Лорис-Меликов 11. Четвертый шаг – планирование исследования. Во всяком деле, чтобы добиться успеха, нужна некоторая доля безумия. Шекспир Уилья
11. Четвертый шаг – планирование исследования. Во всяком деле, чтобы добиться успеха, нужна некоторая доля безумия. Шекспир Уилья Презентация на тему Московский Кремль
Презентация на тему Московский Кремль  МК-Малая академия-2019 (новые филиалы без ЛЛ) (4)
МК-Малая академия-2019 (новые филиалы без ЛЛ) (4) Спирты и фенолы
Спирты и фенолы Что такое биомеханика
Что такое биомеханика  Презентация на тему Природная зональность
Презентация на тему Природная зональность  Урок-олимпиада «Кто хочет стать грамотным?»
Урок-олимпиада «Кто хочет стать грамотным?» Анализ социального института собеседования при приеме на работу
Анализ социального института собеседования при приеме на работу Nightrider
Nightrider Г.Цыферов «Как цыплёнок впервые сочинил сказку»
Г.Цыферов «Как цыплёнок впервые сочинил сказку» Якутское национальное блюдо саламат
Якутское национальное блюдо саламат Wildlife of the UK
Wildlife of the UK Что мы знаем о Солнце?
Что мы знаем о Солнце? Роль баскетбола в развитии физического качества ловкость у учащихся среднего школьного возраста
Роль баскетбола в развитии физического качества ловкость у учащихся среднего школьного возраста САПР
САПР Компонентная среда разработки инструментария нагрузочного тестирования
Компонентная среда разработки инструментария нагрузочного тестирования Компетентность, универсальные учебные действия и практика проектирования учебного процесса
Компетентность, универсальные учебные действия и практика проектирования учебного процесса Изменение климата
Изменение климата Тема 2.2 Поводження із психічно хворими людьми
Тема 2.2 Поводження із психічно хворими людьми