Сумма (разность) функций

Содержание
Определение
Алгоритм построения (сумма функций)
Пример №1
Алгоритм построения (разность функций)
Пример №2
Выполнить построение
Выход

Сумма функций
Суммой функций ƒ(x) и g(x) называется функция h(x) с областью определения, являющейся общей частью областей определения ƒ(x) и g(x), при этом значении функции h(x) равны ƒ(x) + g(x).

Построение
графика функции h(x)= ƒ(x) + g(x):
Построить график функции y=ƒ(x)
В той же системе координат построить график функци y=g(x)
В каждой точке к отрезку изображающему ординату первого графика, пристроить отрезок, изображающий ординату второго графика.

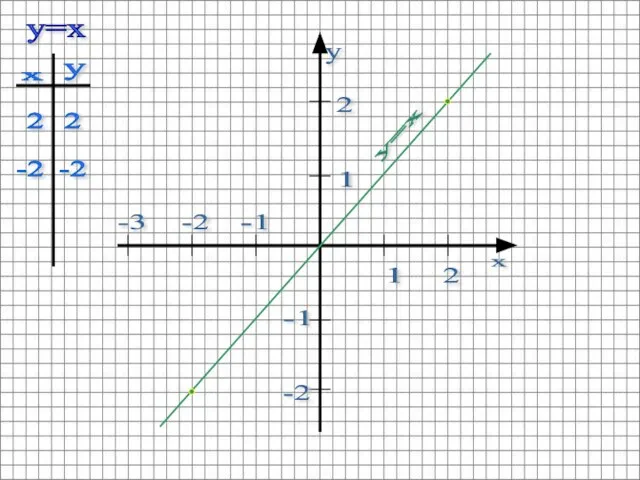
Пример:
Построить график функции y=x+1/x
Строим график функции y=x
Графиком этой функции является прямая. Биссектриса I и III координатных углов.

y=x
1
2
2
1
-2
-1
-2
-3
-1
2
-2
2
-2
y=x

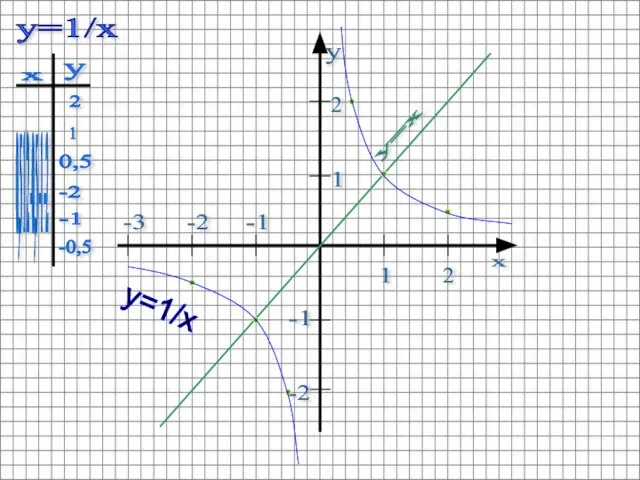
В той же системе координат строим график функции y=1/x.
Графиком этой функции является гипербола, располагающаяся в I и III координатных четвертях.

y=x
1
2
2
1
-2
-1
-2
-3
-1
y=1/x
0,5 1 2 -0,5 -1 -2
y=1/x
-0,5
-1
-2
0,5
1
2

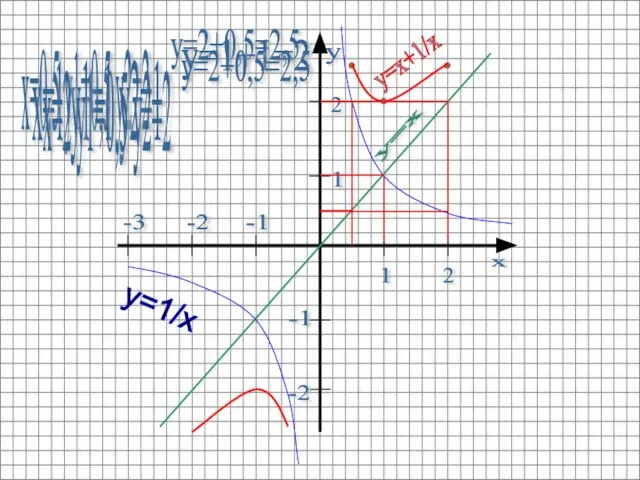
Для каждого значения x (x≠0) складываем длины соответствующих отрезков, изображающих ординаты.

y=x
x=0,5 y1=0,5 y2=2
1
2
2
1
-2
-1
-2
-3
-1
y=1/x
y=2+0,5=2,5
x=1 y1=1 y2=1
y=1+1=2
x=2 y1=0,5 y2=2
y=2+0,5=2,5
y=x+1/x

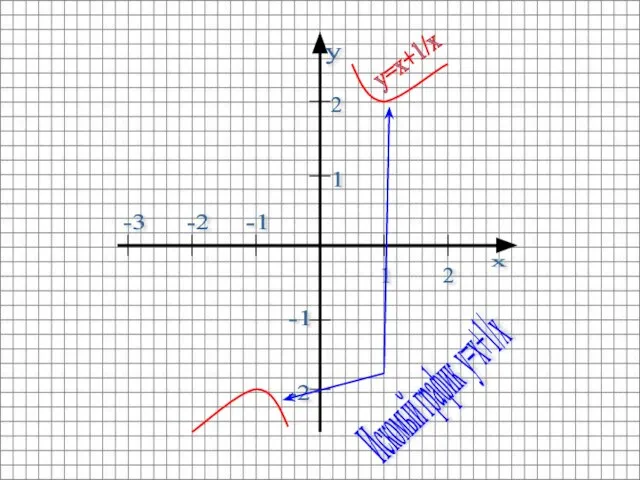
1
2
2
1
-2
-1
-2
-3
-1
y=x+1/x
Искомый график y=x+1/x

Построение
графика функции h(x)=ƒ(x) - g(x)
Аналогично сумме, определяется разность двух функций и строится её график.
При построении графика разности можно поступить иначе:
Строим график функции y=ƒ(x)
В этой же системе координат строим график функции y=g(x)
График функции y=g(x) отобразить симметрично относительно оси 0x. (тем самым получится график функции y=-g(x))
Сложим графики функций y=ƒ(x) и y=g(x).

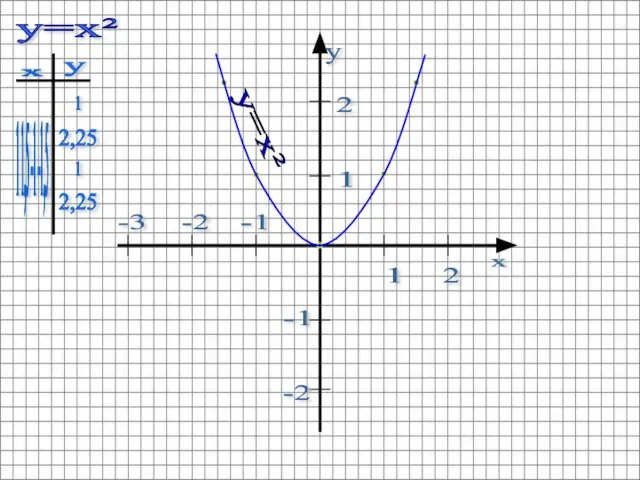
Построить график функции y=x²-x
Строим график функции y=x²
Графиком этой функции является парабола Ветви направлены вверх (т.к. a=1>0)
Вершина находится в точке O(0;0).
Пример 2:

1
2
2
1
-2
-1
-2
-3
-1
y=x²
1 1,5 -1 -1,5
y=x²
1
1
2,25
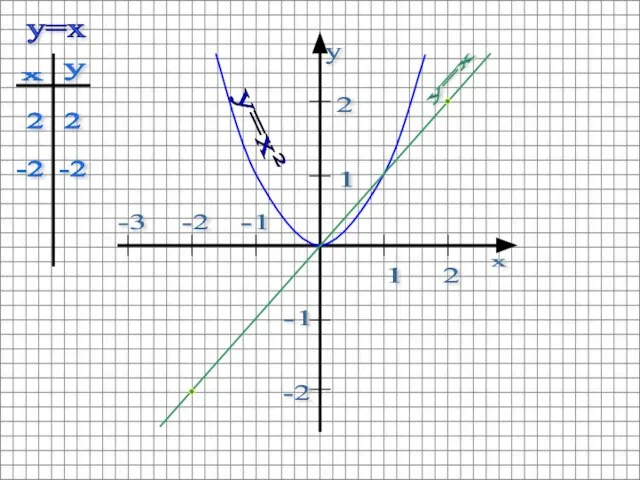
2,25

Строим график функции y=x в той же системе координат
Графиком этой функции является прямая.
Биссектриса I и III координатных углов.

1
2
2
1
-2
-1
-2
-3
-1
y=x²
y=x
2
-2
2
-2
y=x

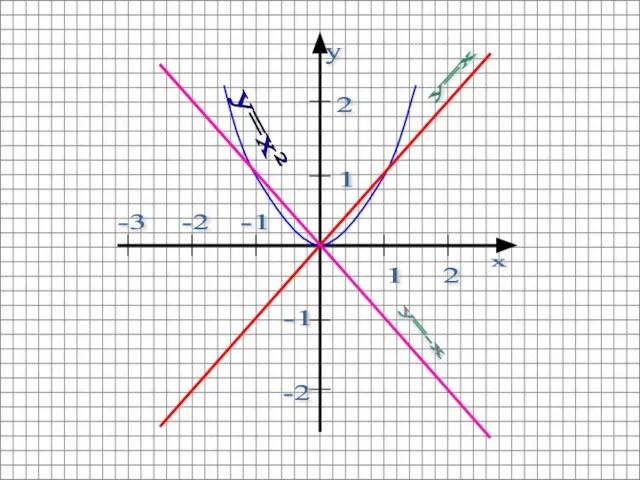
Симметрично отображаем график функции y=x относительно 0x
(в той же системе координат).
Теперь графиком этой функции будет являться прямая, проходящая через II и IV координатные углы.

y=x
1
2
2
1
-2
-1
-2
-3
-1
y=x²
y=-x

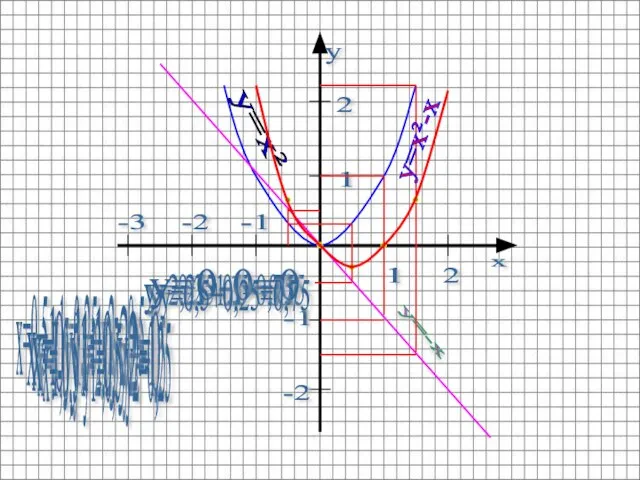
Для каждого значения x складываем соответствующие длины отрезков, изображающие ординаты.

1
2
2
1
-2
-1
-2
-3
-1
y=x²
y=-x
x=0,5 y1=0,25 y2=-0,5
y=0,25-0,5=-0,25
x=1 y1=1 y2=-1
y=1-1=0
x=1,5 y1=2,25 y2=-1,5
y=2,25-1,5=0,75
x=0 y1=0 y2=0
y=0-0=0
x=-0,5 y1=0,5 y2=0,25
y=0,5+0,25=0,75
y=x²-x

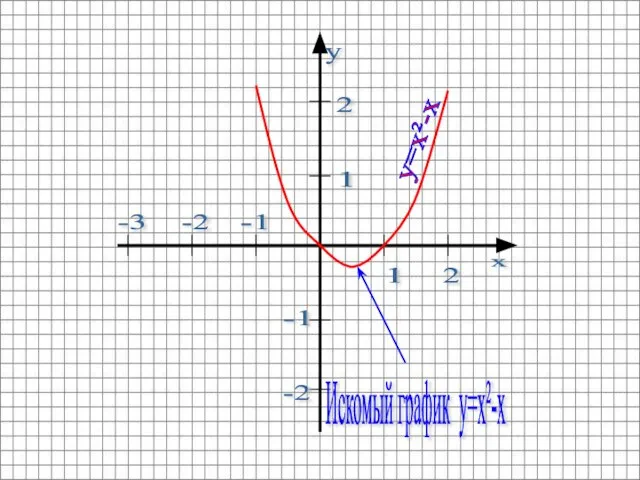
1
2
2
1
-2
-1
-2
-3
-1
y=x²-x
Искомый график y=x²-x