Свойства функции на основе этнокультурного материала.

ЦЕЛИ:
Вспомнить понятие определения функции.
Рассмотреть характерные свойства функции.
Показать аналогию свойств функции с пословицами .
Развить представления о том, что для лучшего запоминания свойств функции можно обратиться к пословицам, ведь пословицы — это отражение устойчивых закономерностей, выверенных многовековым опытом народа.

Ответьте на вопросы:
В каком случае переменную у называют функцией переменной х?
Как при этом называют переменную х?
Что понимают под графиком функции?

ЧЕМ ДАЛЬШЕ В ЛЕС, ТЕМ БОЛЬШЕ ДРОВ.
Математически это записывается так: х 1 < х 2 => F(x1) < F(x2) для всех х, входящих в область оп­ределения.

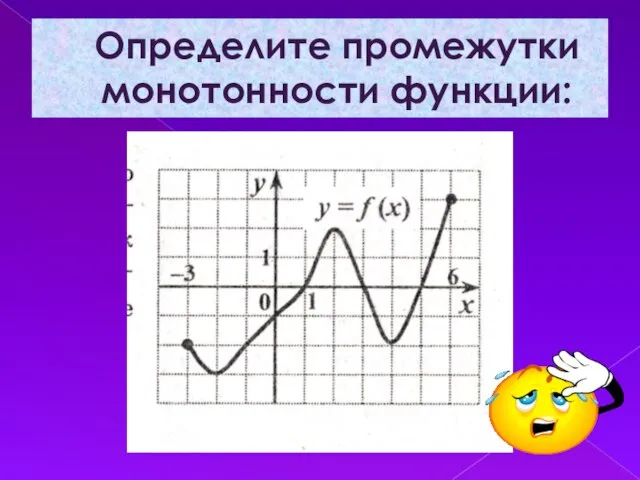
Определите промежутки монотонности функции:

ВЫШЕ МЕРЫ КОНЬ НЕ СКАЧЕТ.

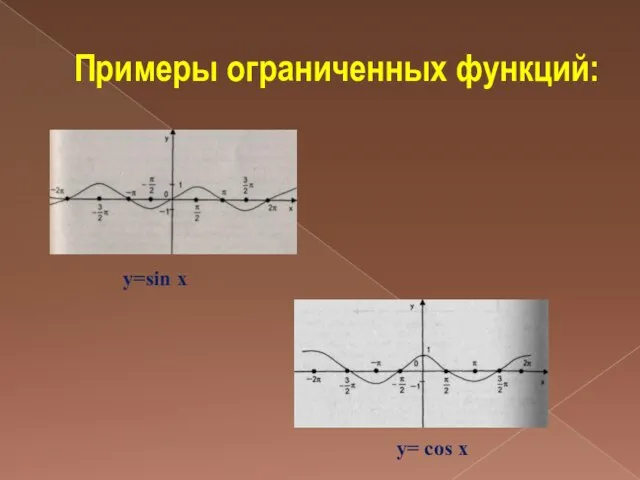
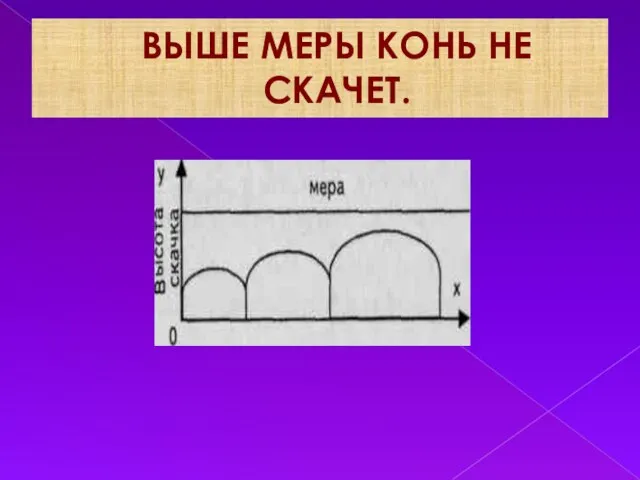
Примеры ограниченных функций:

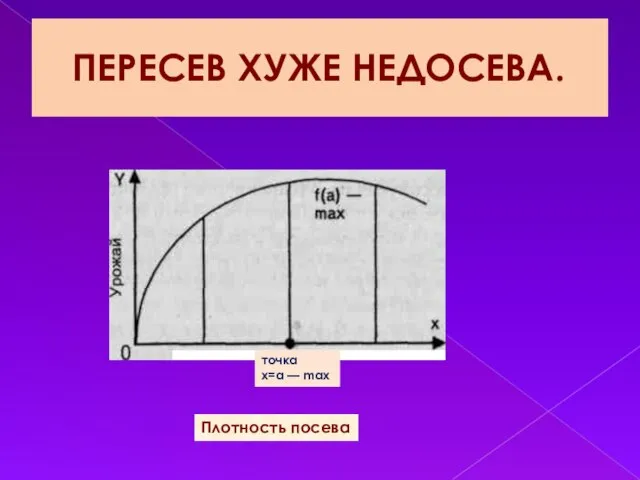
ПЕРЕСЕВ ХУЖЕ НЕДОСЕВА.
Плотность посева
точка
х=а — max

Максимум (max) — это наибольшее значение функции по сравнению с ее значениями во всех соседних точках. Это как бы вершина горы, с которой все дороги ведут только вниз, куда ни шагни.
Есть у max антипод — rain. Минимум — это как бы впадина, из которой куда ни шагни — все дороги ведут только вверх

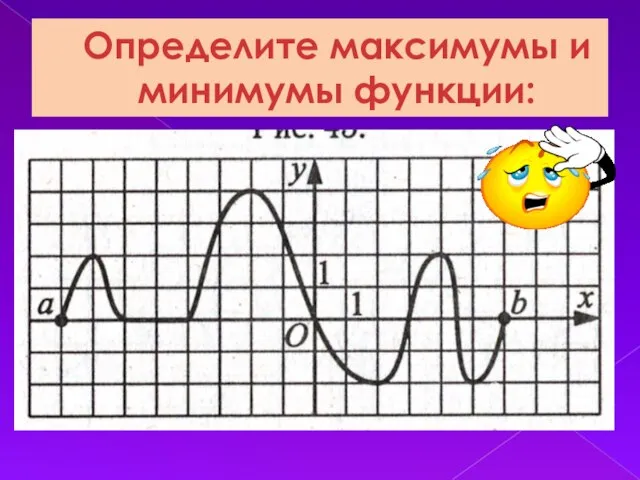
Определите максимумы и минимумы функции:

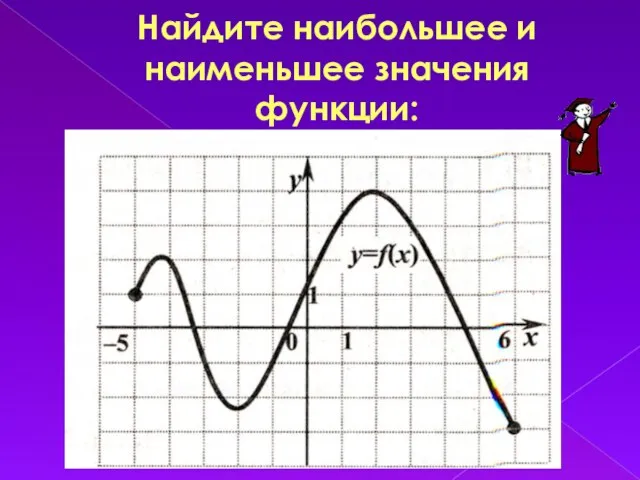
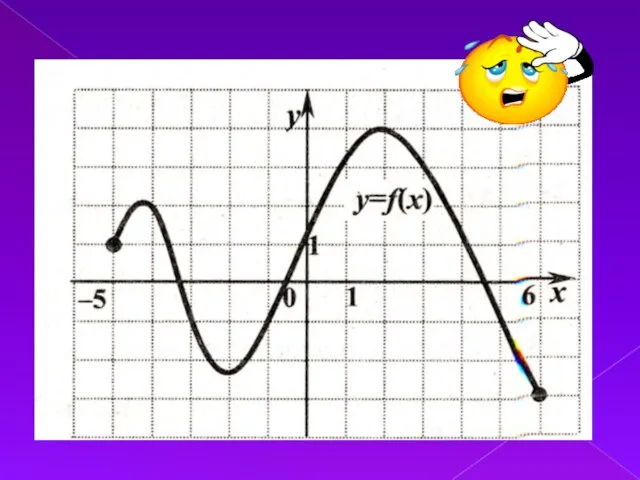
Найдите наибольшее и наименьшее значения функции:

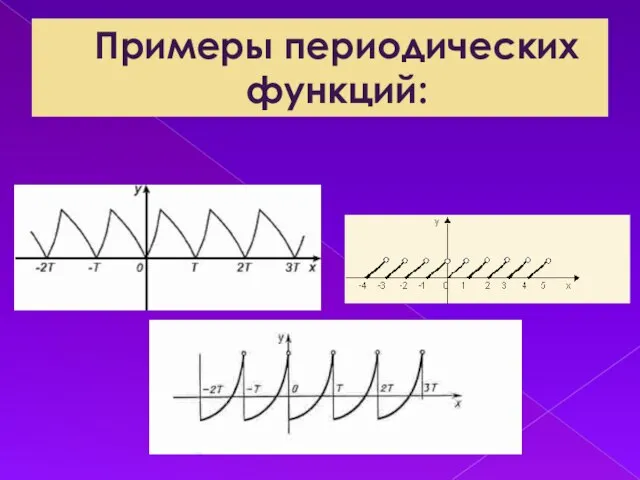
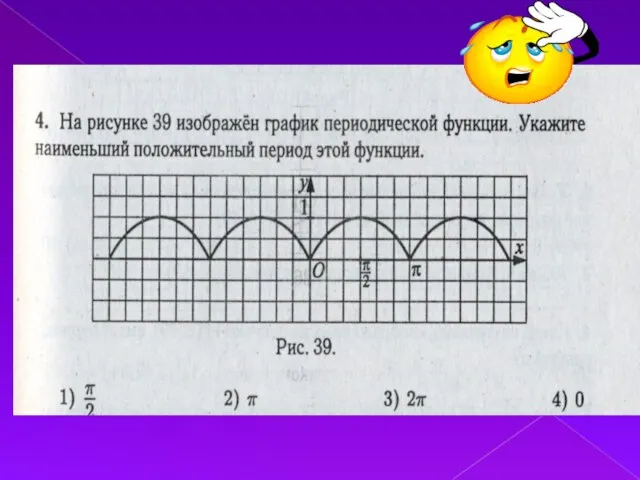
ПЕРИОДИЧНОСТЬ ФУНКЦИИ.
Периодичностью в обыденной жизни называют всякую повторяемость. Но повторяемость может быть более или менее строгой. Строгим является выражение «периодическая печать». Газеты выходят день за днем. Журналы печатаются из месяца в месяц, из недели в неделю. Однако абсолютной строгости понятие периода тут не достигает. Оно было бы здесь лишь тогда, когда время выхода соблюдалось бы с абсолютной точностью, а тексты полностью совпадали. Безупречные примеры пе­риодичности способна дать только математика.

Примеры периодических функций:

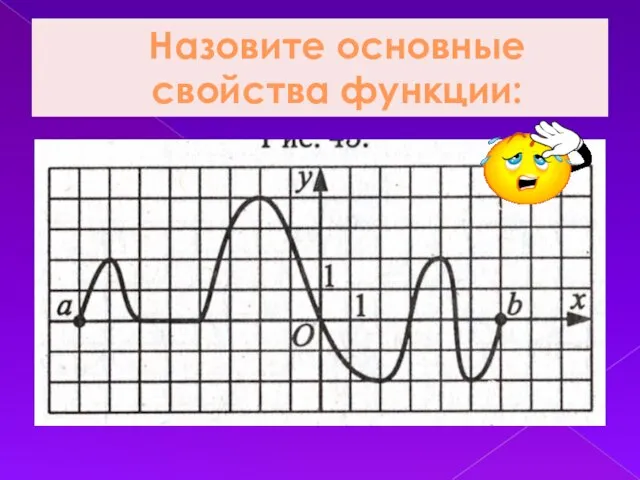
Назовите основные свойства функции: