Содержание
- 2. Цели урока: повторить раннее изученные свойства функции у=tgx; научиться строить график функции у=tgx, используя данные свойства
- 3. Функция y=tg x и её свойства. 1. Обл. определения: . 2. Множество значений функции: уєR. 3.
- 4. Функция y=tg x возрастает на промежутке 1. Пусть 0 ≤ x1 2. Т. к. функция у=sin
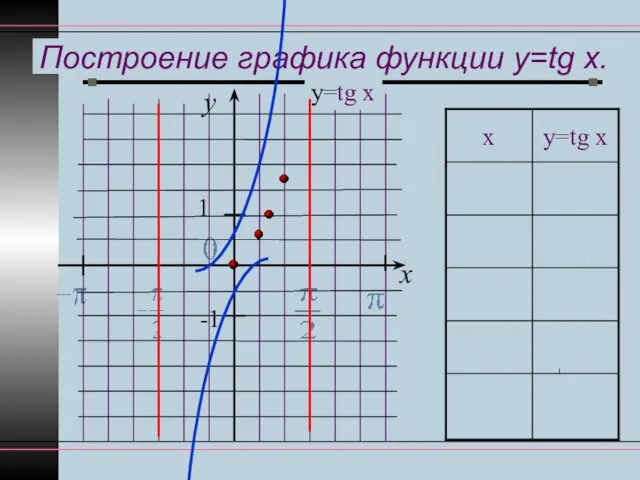
- 5. Построение графика функции y=tg x. y x 1 -1 у=tg x
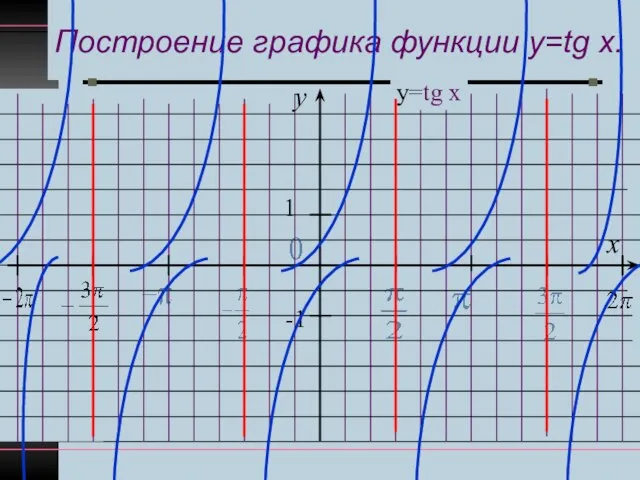
- 6. Построение графика функции y=tg x. y x 1 -1 у=tg x
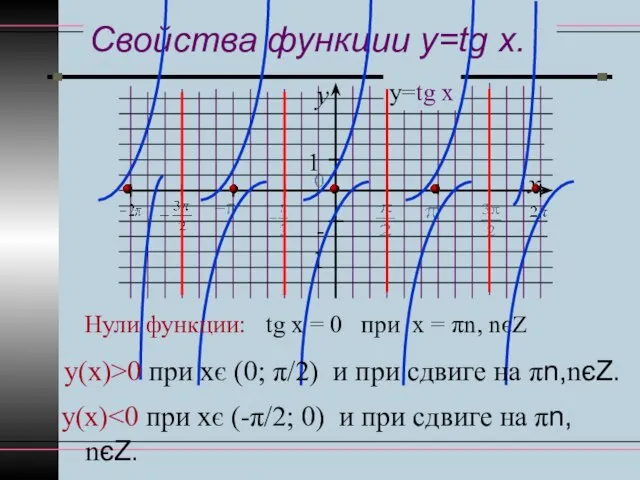
- 7. Свойства функции y=tg x. y x 1 -1 у=tg x Нули функции: tg х = 0
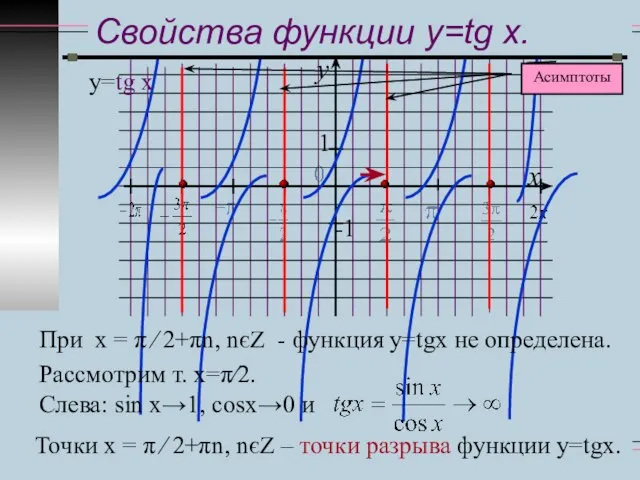
- 8. y x 1 -1 Свойства функции y=tg x. у=tg x При х = π ∕ 2+πn,
- 9. Свойства функции y=tgx. 1. Обл. определения: . 2. Множество значений функции: уєR. 3. Периодическая, Т= π.
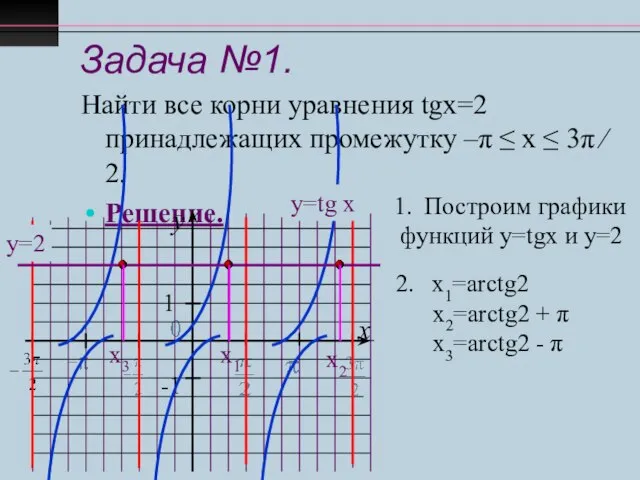
- 10. Задача №1. Найти все корни уравнения tgx=2 принадлежащих промежутку –π ≤ х ≤ 3π ∕ 2.
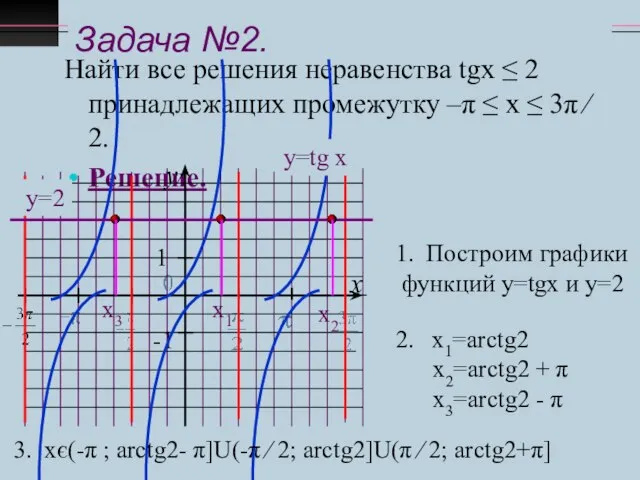
- 11. Задача №2. Найти все решения неравенства tgx ≤ 2 принадлежащих промежутку –π ≤ х ≤ 3π
- 13. Скачать презентацию




 Прикладные, или практико-ориентированные проекты
Прикладные, или практико-ориентированные проекты Множественность денежных единиц
Множественность денежных единиц Научные направления химфакультета
Научные направления химфакультета Презентация на тему Сферы жизнедеятельности общества
Презентация на тему Сферы жизнедеятельности общества  Надя Дорофеева и Алексей Завгородний
Надя Дорофеева и Алексей Завгородний культура скіфів
культура скіфів Черновой вариант законопроекта о самозанятых, партия Единая Россия
Черновой вариант законопроекта о самозанятых, партия Единая Россия Разработка программного обеспечения для решения задач теплотехники
Разработка программного обеспечения для решения задач теплотехники Символизм тайной доктрины. Теософское общество
Символизм тайной доктрины. Теософское общество Применение сжатого воздуха
Применение сжатого воздуха Отчет о проделанной работе за 2010 год отделом охраны, воспроизводства природных комплексов и природопользования ГУ ГПР «Акжайык
Отчет о проделанной работе за 2010 год отделом охраны, воспроизводства природных комплексов и природопользования ГУ ГПР «Акжайык Лекция №5
Лекция №5 Вода - символ жизни. Опыты с водой
Вода - символ жизни. Опыты с водой Глобальные конкурентные стратегии
Глобальные конкурентные стратегии Семинар
Семинар НЛО
НЛО Моя история. С чего все начиналось
Моя история. С чего все начиналось Особенности финансов кредитных организаций
Особенности финансов кредитных организаций Презентация на тему Рекомендации родителям по укреплению здоровья детей
Презентация на тему Рекомендации родителям по укреплению здоровья детей В гостях у басни
В гостях у басни Трансляция розничным потребителям платы за мощность на оптовом рынке. Общие принципы, нормативная конструкция
Трансляция розничным потребителям платы за мощность на оптовом рынке. Общие принципы, нормативная конструкция Т Е С Т по правилам техники безопасности и предупреждения травматизма при проведении занятий по гимнастике.
Т Е С Т по правилам техники безопасности и предупреждения травматизма при проведении занятий по гимнастике. Різноманітність рослин у природі
Різноманітність рослин у природі ENGLISH creativity CLUB
ENGLISH creativity CLUB « Мы за чаем, не скучаем!»
« Мы за чаем, не скучаем!» От адаптивного управления до искусственного интеллекта
От адаптивного управления до искусственного интеллекта  УПРАВЛЕНИЕ СТРАТЕГИЧЕСКИМ РАЗВИТИЕМ МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ Фролова Н.С – ведущий экономист Дальневосточного научно-исслед
УПРАВЛЕНИЕ СТРАТЕГИЧЕСКИМ РАЗВИТИЕМ МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ Фролова Н.С – ведущий экономист Дальневосточного научно-исслед Решение неравенств первой степени с одной переменной
Решение неравенств первой степени с одной переменной