Тела вращения

Концы отрезка АВ, равного а, лежат на окружностях основания цилиндра. Радиус цилиндра равен r, высота h, расстояние между прямой АВ и осью ОО1 цилиндра равно d.
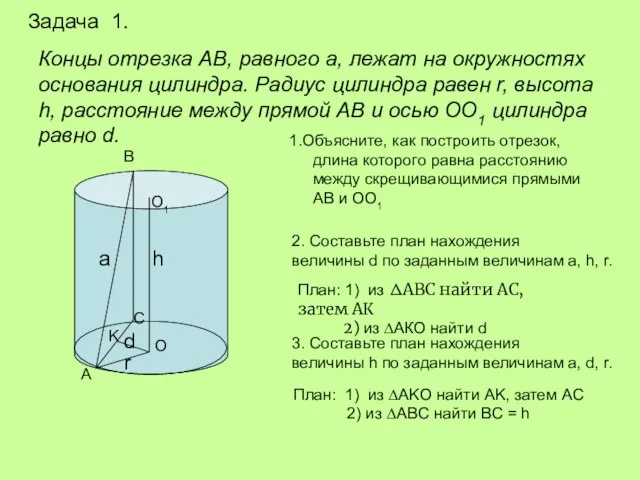
1.Объясните, как построить отрезок, длина которого равна расстоянию между скрещивающимися прямыми АВ и ОО1
А
В
О
О1
а
h
r
C
K
d
2. Составьте план нахождения
величины d по заданным величинам a, h, r.
План: 1) из ∆АВС найти АС, затем АК
2) из ∆АКО найти d
3. Составьте план нахождения
величины h по заданным величинам a, d, r.
План: 1) из ∆АKO найти АK, затем АC
2) из ∆АBC найти BC = h
Задача 1.

Задача 2.
Плоскость γ, параллельная оси цилиндра, отсекает от
окружности основания дугу AmD с градусной мерой α.
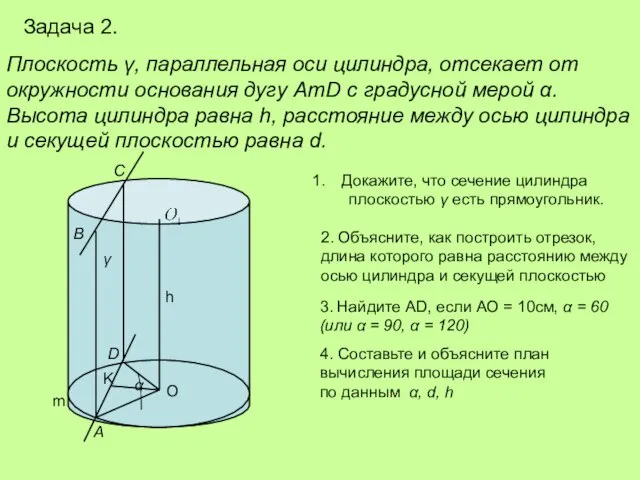
Высота цилиндра равна h, расстояние между осью цилиндра
и секущей плоскостью равна d.
γ
D
В
А
С
O
m
α
K
h
Докажите, что сечение цилиндра
плоскостью γ есть прямоугольник.
2. Объясните, как построить отрезок,
длина которого равна расстоянию между
осью цилиндра и секущей плоскостью
3. Найдите AD, если АО = 10см, α = 60
(или α = 90, α = 120)
4. Составьте и объясните план
вычисления площади сечения
по данным α, d, h

Задача 3.
Высота конуса равна h. Через образующие МА и МВ
проведена плоскость, составляющая угол α с плоскостью
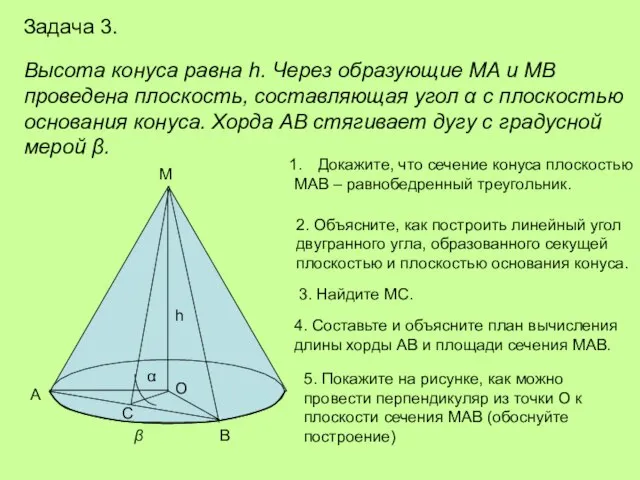
основания конуса. Хорда АВ стягивает дугу с градусной
мерой β.
h
С
α
В
А
М
Докажите, что сечение конуса плоскостью
МАВ – равнобедренный треугольник.
2. Объясните, как построить линейный угол
двугранного угла, образованного секущей
плоскостью и плоскостью основания конуса.
3. Найдите МС.
4. Составьте и объясните план вычисления
длины хорды АВ и площади сечения МАВ.
β
5. Покажите на рисунке, как можно
провести перпендикуляр из точки О к
плоскости сечения МАВ (обоснуйте
построение)
О

Задача 4.
Вершины треугольника АВС лежат на сфере, радиус
которой равен 13. Найти расстояние от центра сферы
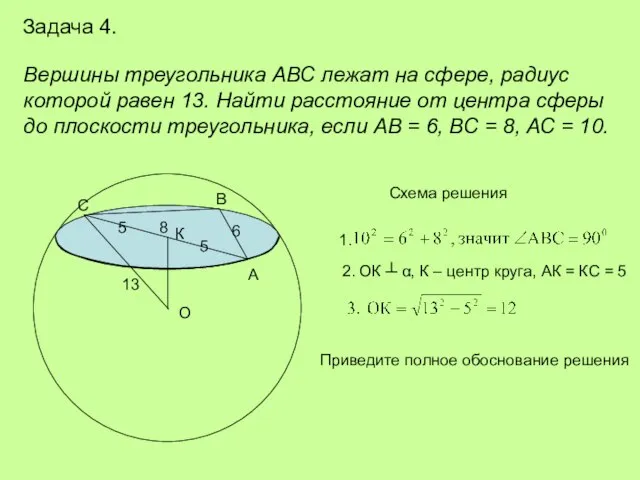
до плоскости треугольника, если АВ = 6, ВС = 8, АС = 10.
С
В
А
К
О
13
8
6
5
5
Схема решения
2. ОК ┴ α, К – центр круга, АК = КС = 5
Приведите полное обоснование решения