Содержание
- 2. Объёмные тела Оглянись вокруг себя, и ты всюду обнаружишь объёмные тела. Это такие геометрические фигуры, которые
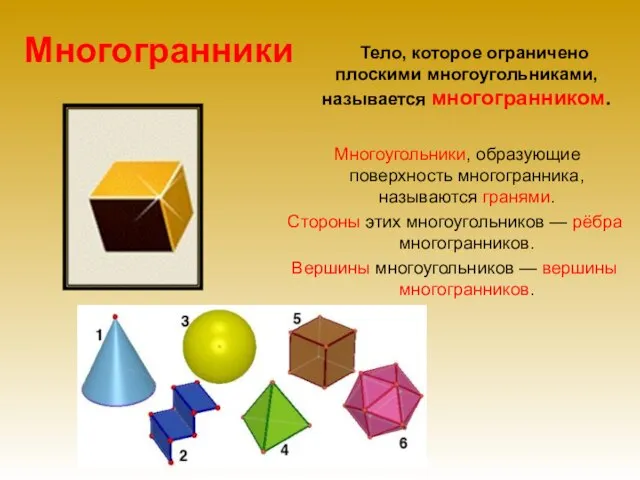
- 3. Многогранники Тело, которое ограничено плоскими многоугольниками, называется многогранником. Многоугольники, образующие поверхность многогранника, называются гранями. Стороны этих
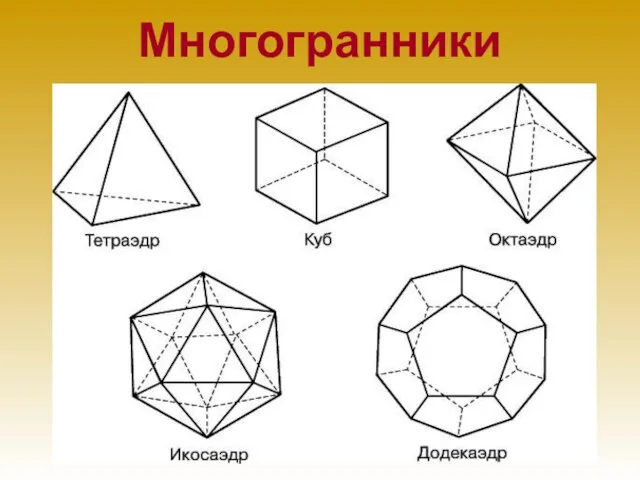
- 4. Многогранники
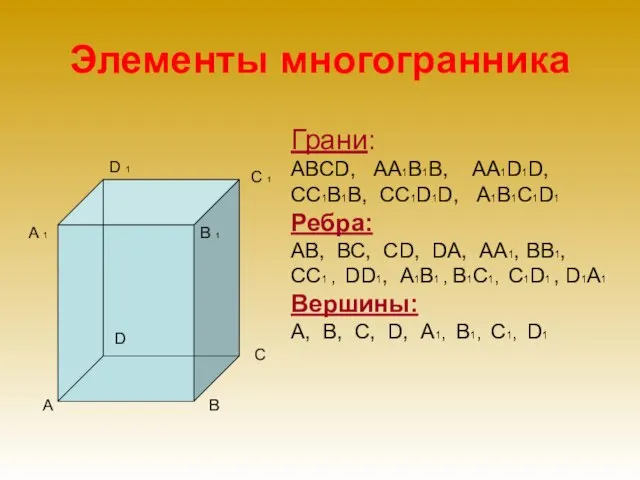
- 5. Элементы многогранника В 1 А В С Грани: АBСD, АА1В1В, АА1D1D, СС1В1В, СС1D1D, А1В1С1D1 Ребра: АB,
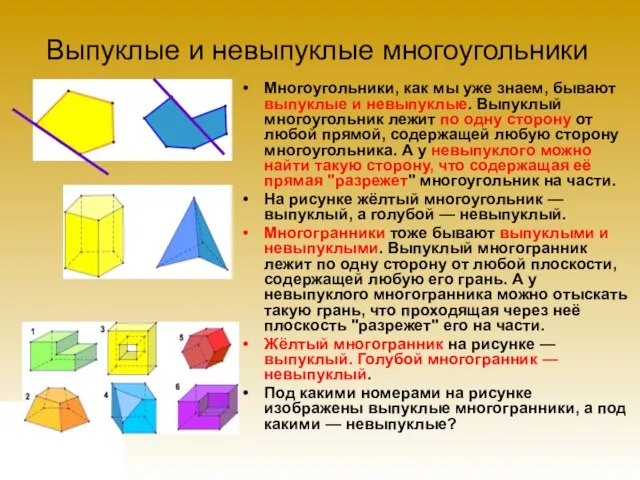
- 6. Выпуклые и невыпуклые многоугольники Многоугольники, как мы уже знаем, бывают выпуклые и невыпуклые. Выпуклый многоугольник лежит
- 7. ПИРАМИДА
- 8. Многогранники. Пирамида. Многогранник справа имеет специальное название: правильная четырёхугольная пирамида. Именно такую форму имеет знаменитая пирамида
- 9. Историческая справка Еги́петские пирами́ды — величайшие архитектурные памятники Древнего Египта, среди которых одно из «семи чудес
- 10. Пирамида Пирамида это многогранник, одна грань которого является произвольным многоугольником (треугольником, или четырёхугольником, или пятиугольником, или
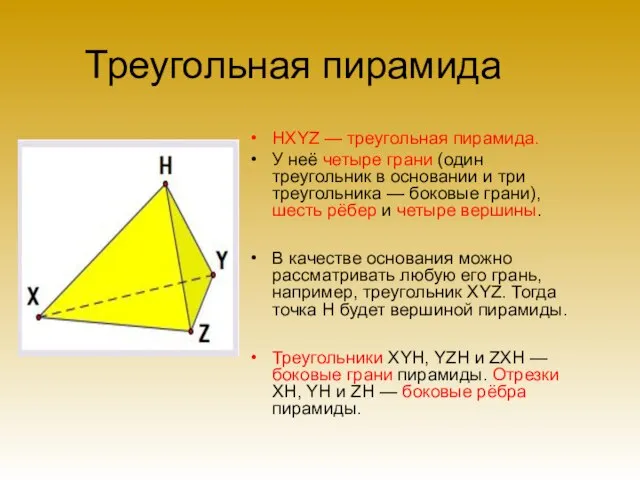
- 11. Треугольная пирамида HXYZ — треугольная пирамида. У неё четыре грани (один треугольник в основании и три
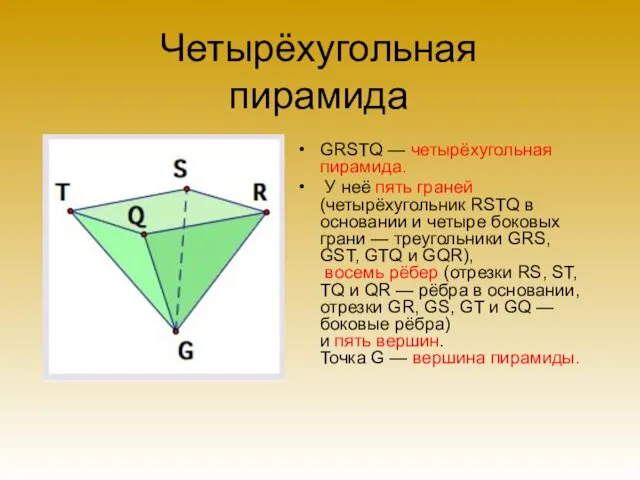
- 12. Четырёхугольная пирамида GRSTQ — четырёхугольная пирамида. У неё пять граней (четырёхугольник RSTQ в основании и четыре
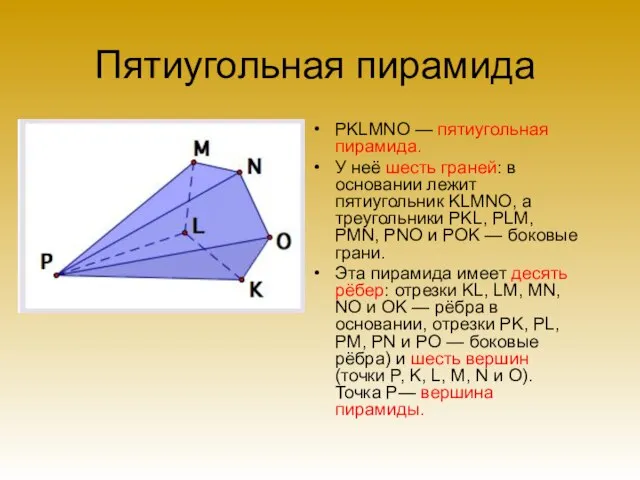
- 13. Пятиугольная пирамида PKLMNO — пятиугольная пирамида. У неё шесть граней: в основании лежит пятиугольник KLMNO, а
- 14. Невыпуклая пирамида На рисунке слева расположена невыпуклая пятиугольная пирамида. В её основании лежит невыпуклый пятиугольник. Все
- 15. Некоторые из многогранников на рисунке являются пирамидами, а некоторые — нет. Под какими номерами изображены пирамиды?
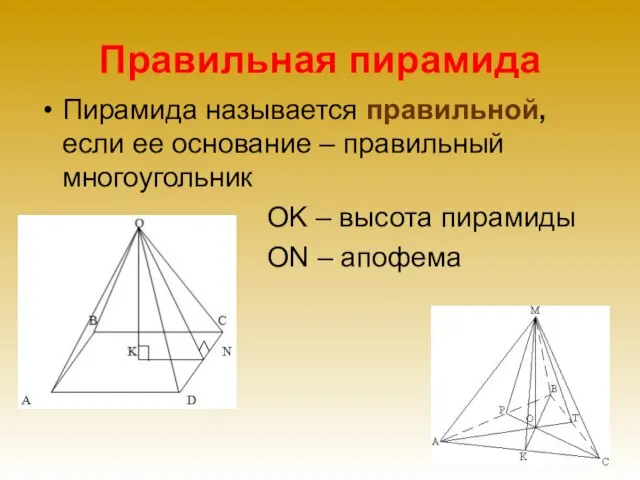
- 16. Правильная пирамида Пирамида называется правильной, если ее основание – правильный многоугольник OK – высота пирамиды ON
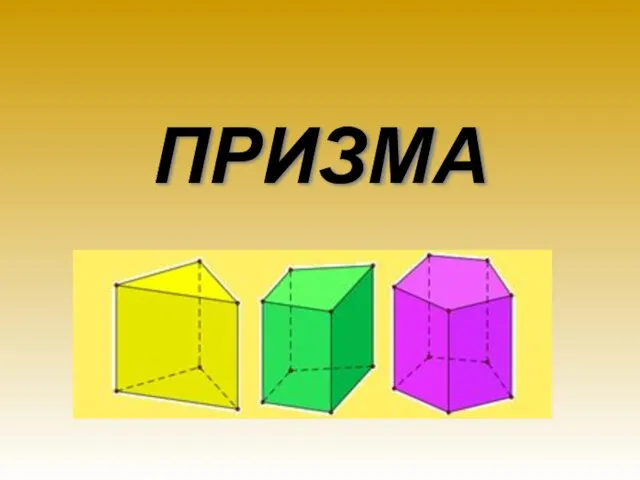
- 17. ПРИЗМА
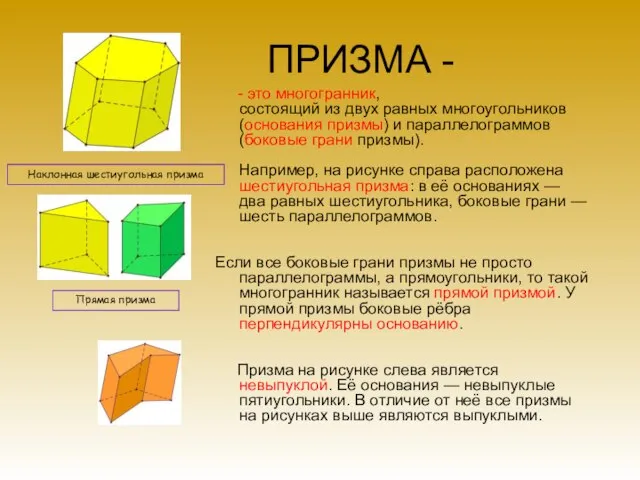
- 18. ПРИЗМА - - это многогранник, состоящий из двух равных многоугольников (основания призмы) и параллелограммов (боковые грани
- 19. Площадь поверхности призмы и площадь боковой поверхности призмы. Поверхность многогранника состоит из конечного числа многоугольников (граней).
- 21. Скачать презентацию








 Отчётность аптек: виды, периодичность
Отчётность аптек: виды, периодичность Новогодний ассортимент 2017-2018
Новогодний ассортимент 2017-2018 Работа с переключателем
Работа с переключателем Литературные премии как ориентир читательских предпочтений
Литературные премии как ориентир читательских предпочтений Ипотечные кредиты от ОАО «Сбербанк России» для участников зарплатных проектов в рамках программы ФЦП «Жилище»
Ипотечные кредиты от ОАО «Сбербанк России» для участников зарплатных проектов в рамках программы ФЦП «Жилище» Изображение воды на плоскости
Изображение воды на плоскости Презентация на тему В. С. Пикуль - боец, труженик, писатель.
Презентация на тему В. С. Пикуль - боец, труженик, писатель. Презентация на тему Японское море
Презентация на тему Японское море Фестиваль Сибирское PROдвижение
Фестиваль Сибирское PROдвижение Оноре де Бальзак
Оноре де Бальзак Фотодело. Семинар 3
Фотодело. Семинар 3 Преданья старины далекой
Преданья старины далекой Группа внедрения
Группа внедрения Презентация на тему Магнитные свойства вещества
Презентация на тему Магнитные свойства вещества  Презентация по рассказу В.П.Астафьева «Васюткино озеро»
Презентация по рассказу В.П.Астафьева «Васюткино озеро» Отчет (1)
Отчет (1) Немецкий Веркбунд
Немецкий Веркбунд Научная деятельность и разработки лаборатории проф. Деулина Е.А.
Научная деятельность и разработки лаборатории проф. Деулина Е.А. Презентация на тему Красная книга Ставропольского края
Презентация на тему Красная книга Ставропольского края Витражное искусство
Витражное искусство Использование метафорических ассоциативных карт в работе педагога-психолога
Использование метафорических ассоциативных карт в работе педагога-психолога Закономерности работы головного мозга
Закономерности работы головного мозга Мурабаха
Мурабаха Тема урока: Второстепенные члены предложения. Определение
Тема урока: Второстепенные члены предложения. Определение ГОРОДСКОЕ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ
ГОРОДСКОЕ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ Photography in society
Photography in society Приливная электростанция (ПЭС)
Приливная электростанция (ПЭС) Анна Ахматова. Жизнь и творчество
Анна Ахматова. Жизнь и творчество