Тела вращения. Сфера и шар

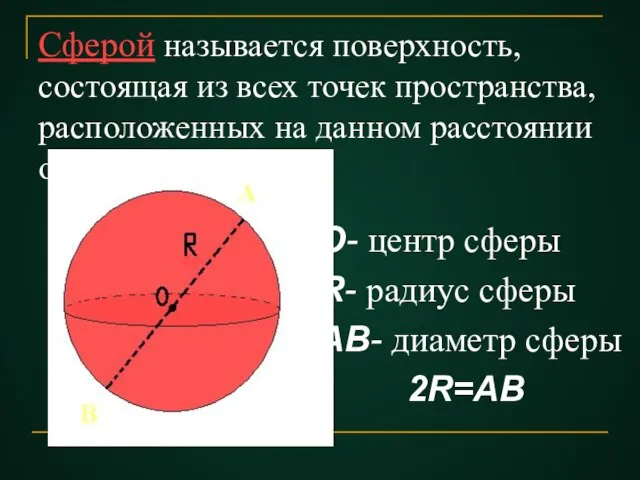
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
О- центр сферы
R- радиус сферы
АВ- диаметр сферы
2R=АВ

Сферу можно получить вращением полуокружности АСВ вокруг диаметра АВ

Шаром называется тело ограниченное сферой.
Центр, радиус и диаметр сферы называются также диаметром шара.
Шар

Задана прямоугольная система координат Оху и дана некоторая поверхность F, например плоскость или сфера . Уравнение с тремя переменными x, у, z называется уравнением поверхности F и не удовлетворяют координаты никакой точки , не лежащей на этой поверхности .
Уравнение сферы
См. далее

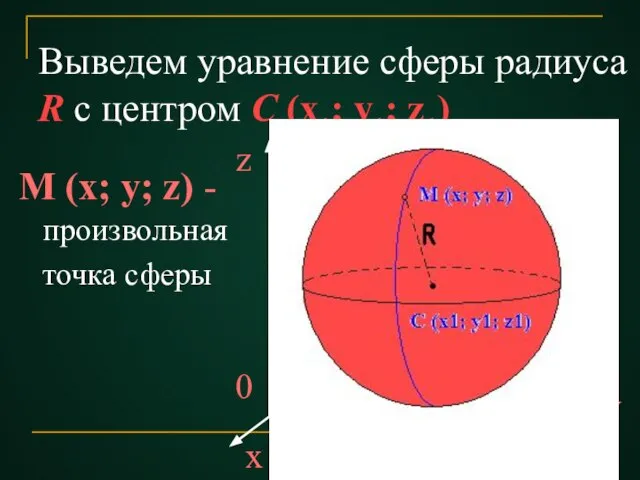
Выведем уравнение сферы радиуса R с центром С (x1; y1; z1)
M (x; y; z) -произвольная точка сферы
x
z
y
0

Расстояние от произвольной точки M (x; y; z)до точки С вычисляем по формуле
МС=√(x-x1)2+(y-y1)2+(z-z1)2

Если точка М лежит на данной сфере , то МС=R, или МС2=R2 т.е. координаты точки М удовлетворяют уравнению:
R2=(x-x1)2+(y-y1)2+(z-z1)2
Если точка М не лежит на данной сфере , то МС2= R2 т.е. координаты точки М не удовлетворяют данного уравнения.

В прямоугольной системе координат уравнение сферы радиуса R с центром С (x1; y1; z1) имеет вид
R2=(x-x1)2+(y-y1)2+(z-z1)2

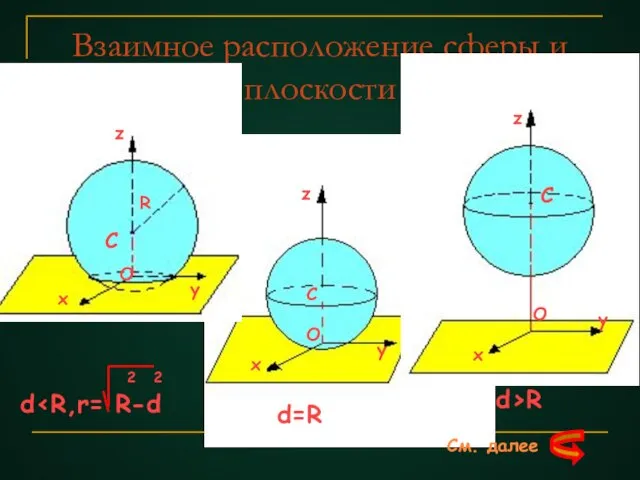
Взаимное расположение сферы и плоскости
Исследуем взаимное расположение сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от её центром до плоскости.

Взаимное расположение сферы и плоскости
z
y
x
O
C
R
y
x
z
C
z
y
x
C
O
O
2 2
d
d=R
d>R
См. далее

Пусть радиус сферы - R, а расстояние
от её центра до плоскости a - d
Введём систему координат, так чтобы плоскость Оху совпадала с плоскостью α ,а центр сферы лежал по Оz , тогда уравнение плоскости α :z=0, а уравнение сферы с учётом (С имеет координаты (0;0;d) )
х2+у 2+(z-d)2=R2

z=0
х2+у 2+(z-d)2=R2
Составим систему уравнений :
Подставив z=0 во второе уравнение , получим :
х2+у 2=R2-d2

Возможны три случая :
1) d
0,
и уравнение
х2+у 2=R2-d2 является уравнением окружности r = √R2-d2 с центром в точке О на плоскости Оху.
В данном случае сфера и плоскость пересекаются по окружности.

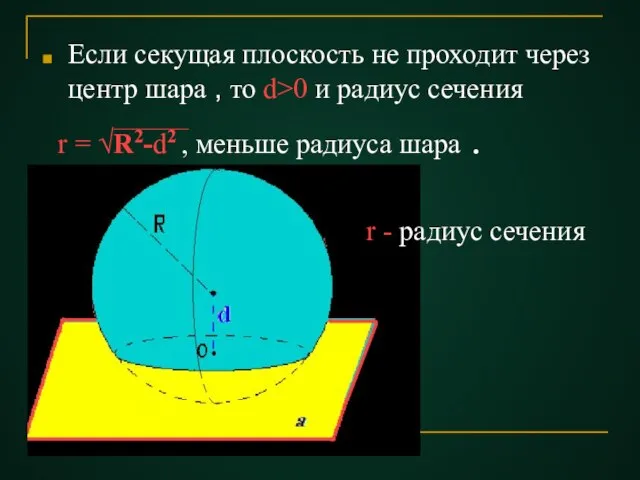
Итак, если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность .

Ясно, что сечение шара плоскостью является круг.
Если секущая плоскость проходит через центр шара, то d=0 и в сечении получается круг радиуса R, т.е. круг , радиус которого равен радиусу шара. Такой круг называется большим кругом шара.

Если секущая плоскость не проходит через центр шара , то d>0 и радиус сечения
r = √R2-d2 , меньше радиуса шара .
r - радиус сечения

2) d=R,тогда R2-d2=0, и уравнению удовлетворяют только
х=0, у=0,
а значит О(0;0;0)удовлетворяют обоим уравнениям ,т.е.
О- единственная общая точка сферы и плоскости .

Итак, если расстояние от центра сферы до плоскости равно радиусу сферы , то сфера и плоскость имеют только одну общую точку.

3) d>R, тогда R2-d2<0, и уравнению х2+у 2=R2-d2 не удовлетворя-ют координаты никакой точки.