Тема: Графы Преподаватель Белгородцева Н.А.

Цель лекции – познакомить студентов:
с основными понятиями и определениями графа и его элементов;
с операциями над графами;
с деревьями, лесом, бинарными деревьями;
со способами задания графа, с изоморфными графами.

2.1. Основные понятия и определения графа и его элементов
Графом называется пара двух конечных множеств: множество точек и множество линий, соединяющих некоторые пары точек.
Точки называются вершинами, или узлами, графа, линии – рёбрами графа.
Если ребро графа G соединяет две его вершины V и W, (т.е. ), то говорят, что это ребро им инцидентно.

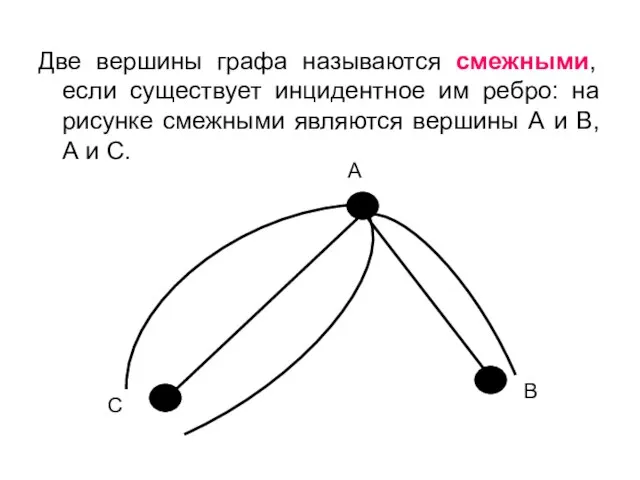
Две вершины графа называются смежными, если существует инцидентное им ребро: на рисунке смежными являются вершины А и В, А и С.

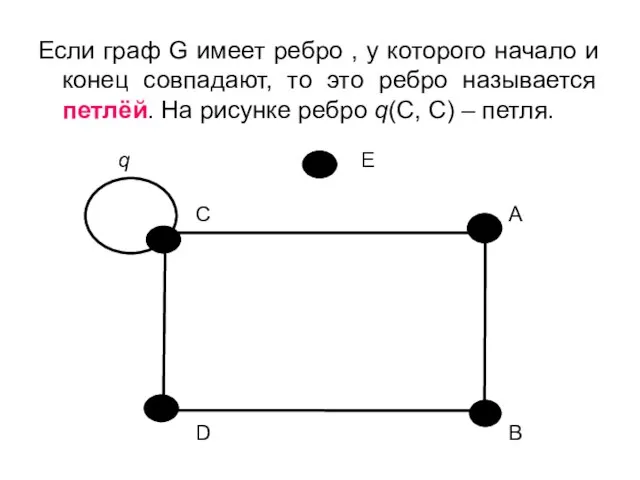
Если граф G имеет ребро , у которого начало и конец совпадают, то это ребро называется петлёй. На рисунке ребро q(С, С) – петля.
С
A
B
D
E
q

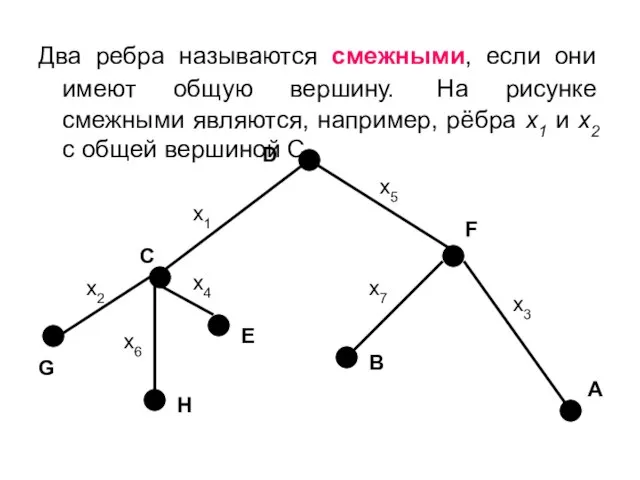
Два ребра называются смежными, если они имеют общую вершину. На рисунке смежными являются, например, рёбра х1 и х2 с общей вершиной С.
х1
х2
х3
х4
х5
х6
х7
С
D
F
A
B
E
H
G

Рёбра, которые начинаются в одной и той же вершине, заканчиваются также в одной и той же вершине, называются кратными, или параллельными. Количество одинаковых пар вида называется кратностью ребра . Число рёбер, инцидентных вершине А, называется степенью этой вершины и обозначается (от англ. degree – степень).

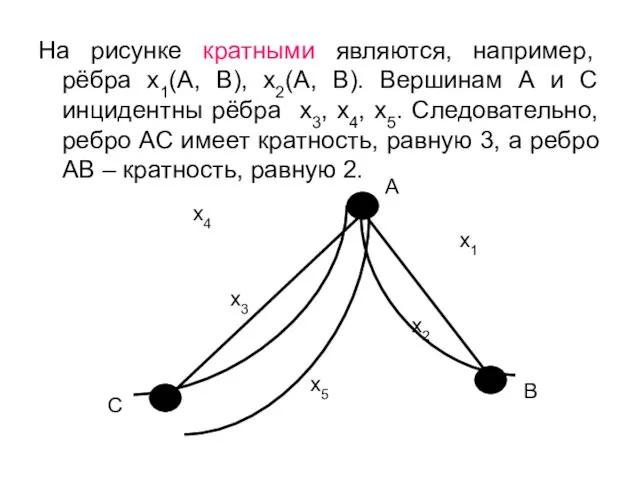
На рисунке кратными являются, например, рёбра х1(А, В), х2(А, В). Вершинам А и С инцидентны рёбра х3, х4, х5. Следовательно, ребро АС имеет кратность, равную 3, а ребро АВ – кратность, равную 2.
А
С
В
х1
х2
х5
х3
х4

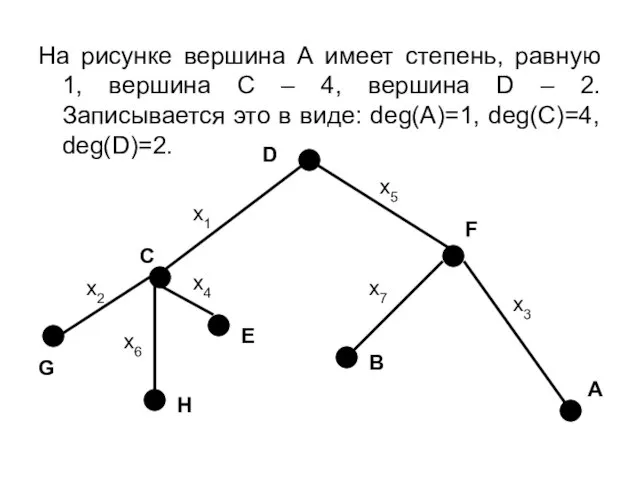
На рисунке вершина А имеет степень, равную 1, вершина С – 4, вершина D – 2. Записывается это в виде: deg(A)=1, deg(C)=4, deg(D)=2.
х1
х2
х3
х4
х5
х6
х7
С
D
F
A
B
E
H
G

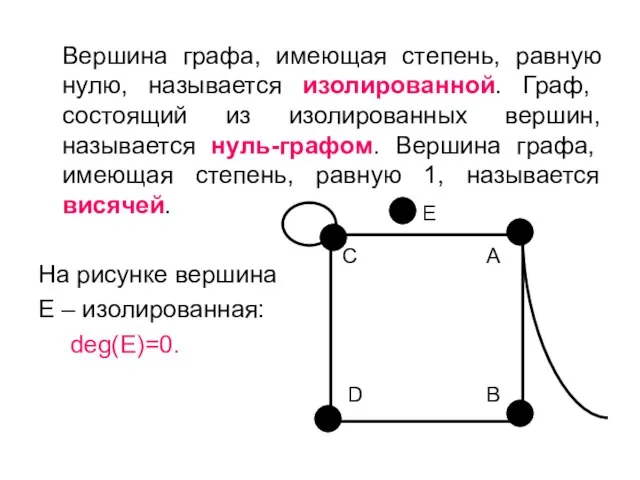
E
Вершина графа, имеющая степень, равную нулю, называется изолированной. Граф, состоящий из изолированных вершин, называется нуль-графом. Вершина графа, имеющая степень, равную 1, называется висячей.
На рисунке вершина
Е – изолированная:
deg(E)=0.
A
B
D
C

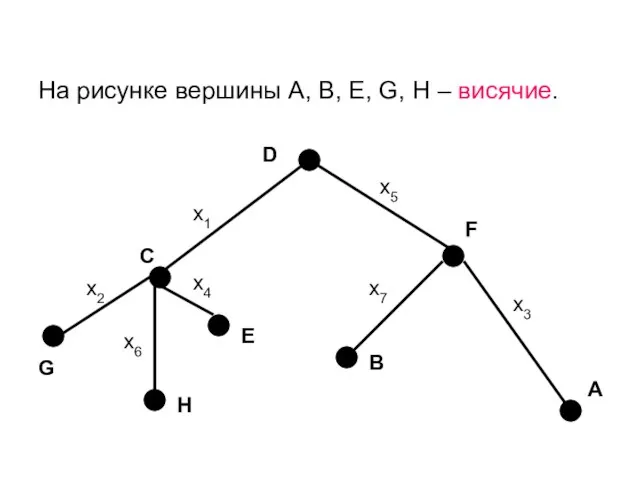
На рисунке вершины А, В, Е, G, H – висячие.
х1
х2
х3
х4
х5
х6
х7
С
D
F
A
B
E
H
G

Теорема 3.1. В графе сумма степеней всех его вершин – число чётное, равное удвоенному числу рёбер графа:
где - число вершин;
- число рёбер графа.

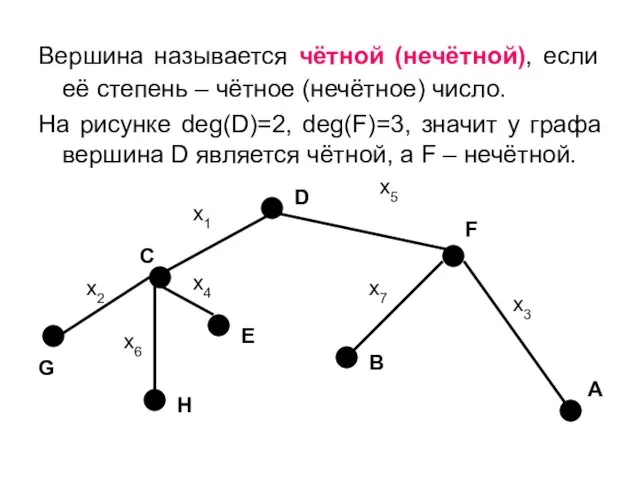
Вершина называется чётной (нечётной), если её степень – чётное (нечётное) число.
На рисунке deg(D)=2, deg(F)=3, значит у графа вершина D является чётной, а F – нечётной.
х1
х2
х3
х4
х5
х6
х7
С
D
F
A
B
E
H
G

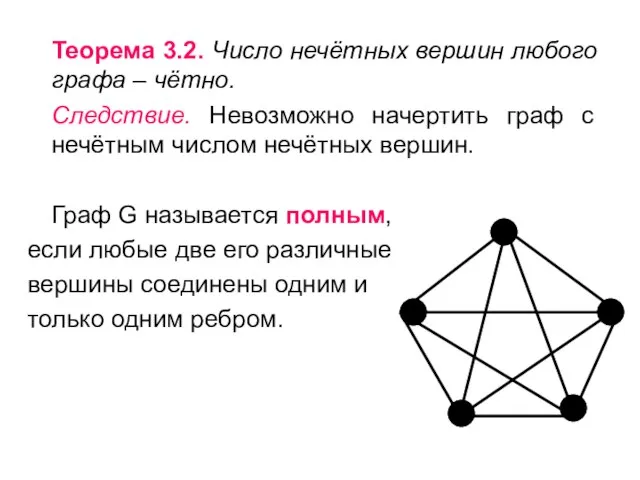
Теорема 3.2. Число нечётных вершин любого графа – чётно.
Следствие. Невозможно начертить граф с нечётным числом нечётных вершин.
Граф G называется полным,
если любые две его различные
вершины соединены одним и
только одним ребром.

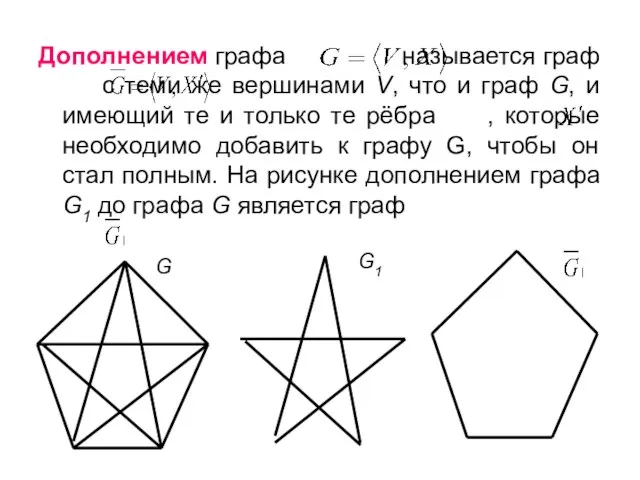
Дополнением графа называется граф с теми же вершинами V, что и граф G, и имеющий те и только те рёбра , которые необходимо добавить к графу G, чтобы он стал полным. На рисунке дополнением графа G1 до графа G является граф
G
G1

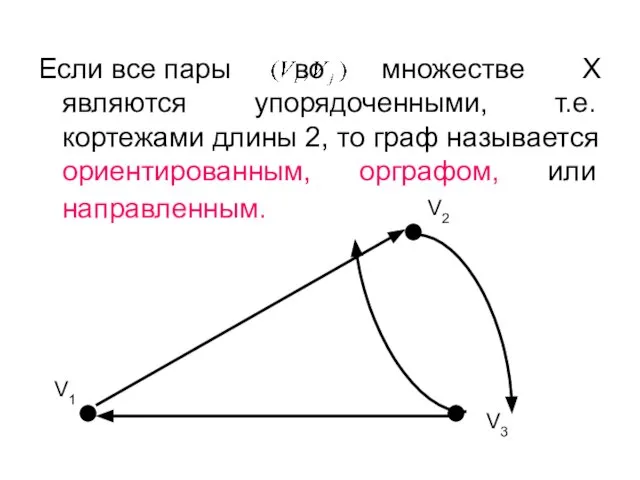
Если все пары во множестве X являются упорядоченными, т.е. кортежами длины 2, то граф называется ориентированным, орграфом, или направленным.

Началом ребра называется вершина, указанная в кортеже первой, концом – вторая вершина этой пары (графически она указана стрелкой). Рёбра ориентированного графа имеют определённые фиксированные начало и конец и называются дугами.
Степенью входа (выхода) вершины ориентированного графа называется число рёбер, для которых эта вершина является концом (началом).
Дуги орграфа называются кратными, если они имеют одинаковые начальные и конечные вершины, т.е. одинаковые направления.

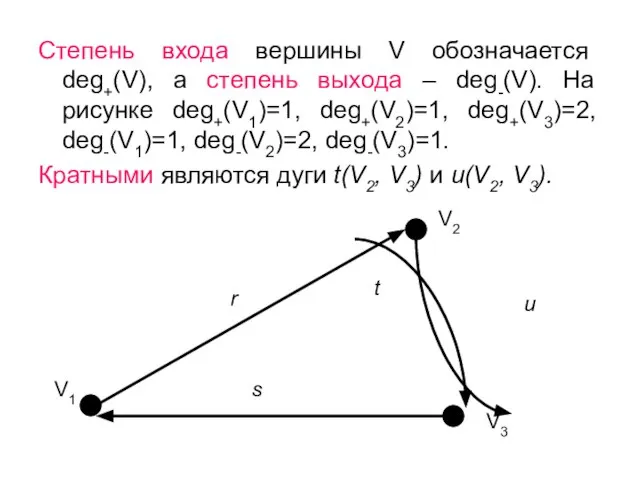
Степень входа вершины V обозначается deg+(V), а степень выхода – deg-(V). На рисунке deg+(V1)=1, deg+(V2)=1, deg+(V3)=2, deg-(V1)=1, deg-(V2)=2, deg-(V3)=1.
Кратными являются дуги t(V2, V3) и u(V2, V3).
V1
V2
V3
t
r
s
u

Последовательность попарно смежных вершин неориентированного графа, т.е. последовательность рёбер неориентированного графа, в которой вторая вершина предыдущего ребра совпадает с первой вершиной следующего, называется маршрутом.
Число рёбер маршрута называется длиной маршрута.
Если начальная вершина маршрута совпадает с конечной, то такой маршрут называется замкнутым или циклом.

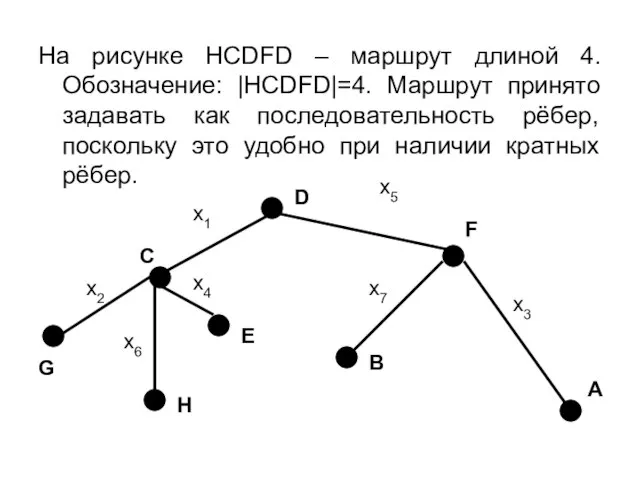
На рисунке HCDFD – маршрут длиной 4. Обозначение: |HCDFD|=4. Маршрут принято задавать как последовательность рёбер, поскольку это удобно при наличии кратных рёбер.
х1
х2
х3
х4
х5
х6
х7
С
D
F
A
B
E
H
G

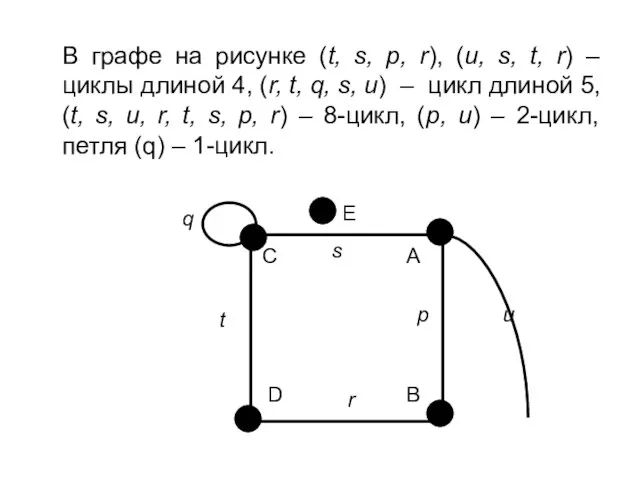
В графе на рисунке (t, s, p, r), (u, s, t, r) – циклы длиной 4, (r, t, q, s, u) – цикл длиной 5, (t, s, u, r, t, s, p, r) – 8-цикл, (p, u) – 2-цикл, петля (q) – 1-цикл.
s

Расстоянием между двумя вершинами называется минимальная длина из длин всех возможных маршрутов между этими вершинами при условии, что существует хотя бы один такой маршрут. Обозначается как (от лат. distantio – расстояние) .
Если любое ребро в маршруте встречается только один раз, то маршрут называется цепью.

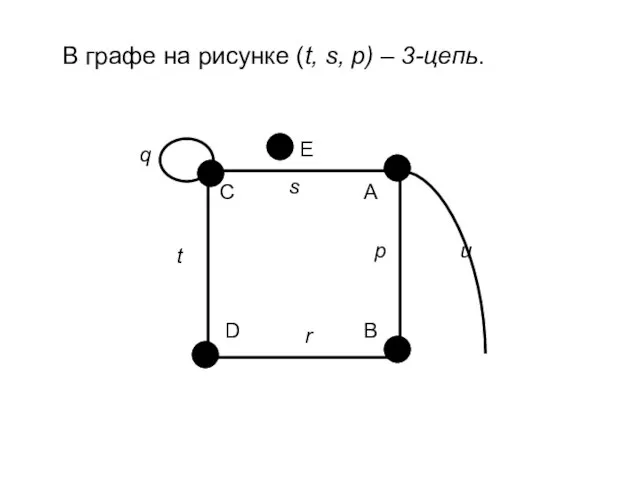
В графе на рисунке (t, s, p) – 3-цепь.

В орграфе маршрут является ориентированным и называется путём.
Путь – упорядоченная последовательность рёбер ориентированного графа, в которой конец предыдущего ребра совпадает с началом следующего и все рёбра единственны.
Цикл в орграфе – путь, у которого совпадают начало и конец.
Цепь, путь и цикл в графе называются простыми, если они проходят через любую из вершин не более одного раза.

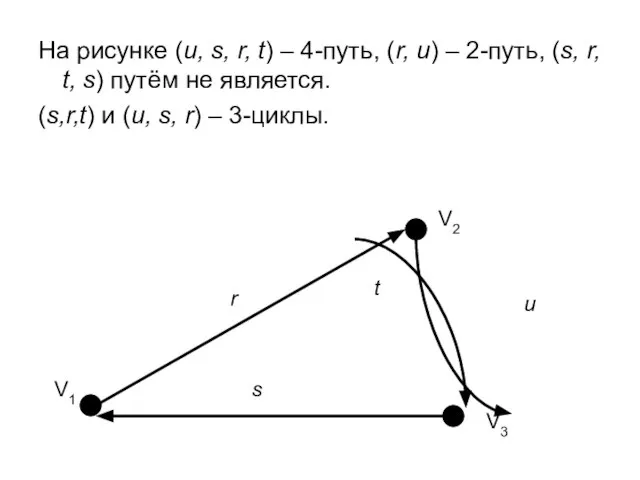
На рисунке (u, s, r, t) – 4-путь, (r, u) – 2-путь, (s, r, t, s) путём не является.
(s,r,t) и (u, s, r) – 3-циклы.
V1
V2
V3
t
r
s
u

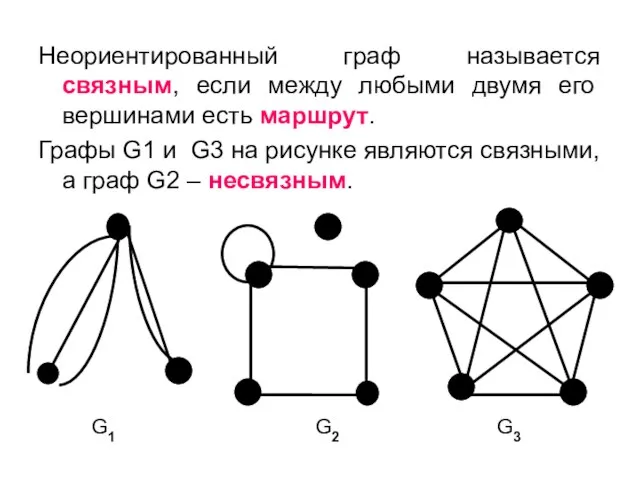
Неориентированный граф называется связным, если между любыми двумя его вершинами есть маршрут.
Графы G1 и G3 на рисунке являются связными, а граф G2 – несвязным.
G1
G2
G3

Две вершины называются связными, если существует маршрут между ними. Связность между вершинами является отношением эквивалентности.
Все подграфы Vi (классы эквивалентности) графа G называют связными компонентами, или компонентами связности.
Теорема 2.3. Для того чтобы связный граф G являлся простым циклом, необходимо и достаточно, чтобы каждая его вершина имела степень, равную 2.

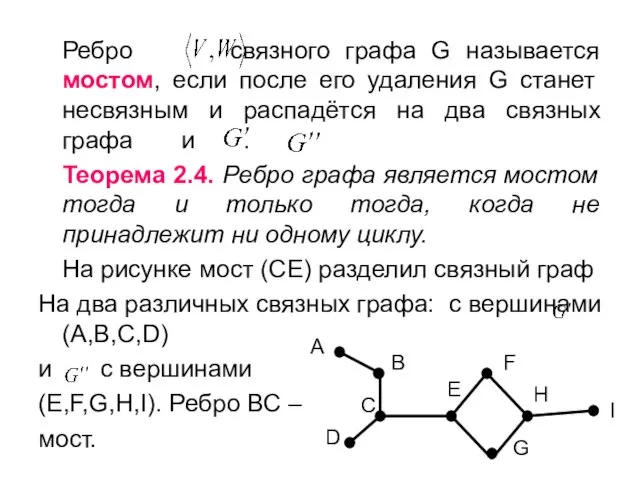
Ребро связного графа G называется мостом, если после его удаления G станет несвязным и распадётся на два связных графа и .
Теорема 2.4. Ребро графа является мостом тогда и только тогда, когда не принадлежит ни одному циклу.
На рисунке мост (СЕ) разделил связный граф
На два различных связных графа: с вершинами (А,В,С,D)
и с вершинами
(E,F,G,H,I). Ребро ВС –
мост.
E

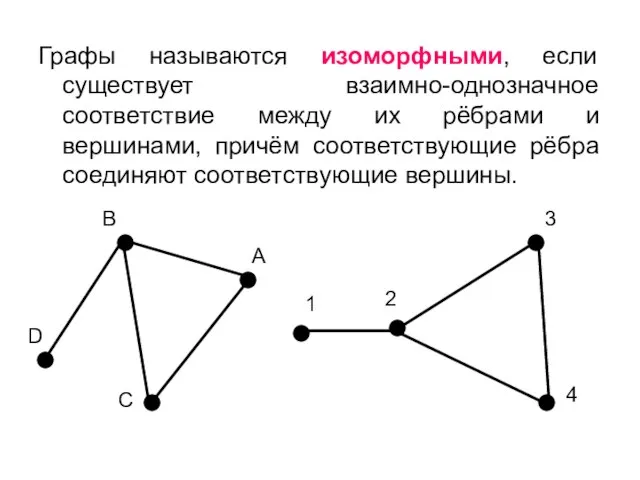
Графы называются изоморфными, если существует взаимно-однозначное соответствие между их рёбрами и вершинами, причём соответствующие рёбра соединяют соответствующие вершины.
D
B
A
C
1
2
3
4

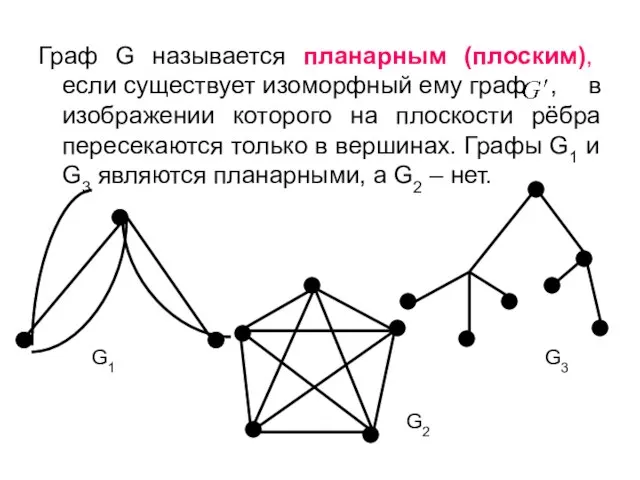
Граф G называется планарным (плоским), если существует изоморфный ему граф , в изображении которого на плоскости рёбра пересекаются только в вершинах. Графы G1 и G3 являются планарными, а G2 – нет.
G1
G2
G3

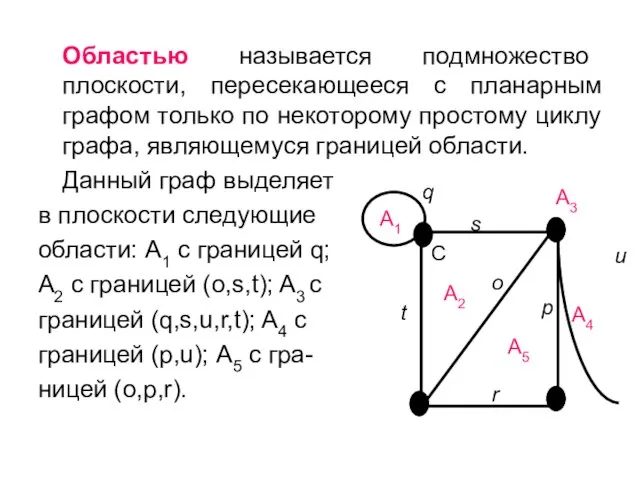
Областью называется подмножество плоскости, пересекающееся с планарным графом только по некоторому простому циклу графа, являющемуся границей области.
Данный граф выделяет
в плоскости следующие
области: А1 с границей q;
А2 с границей (o,s,t); A3 c
границей (q,s,u,r,t); A4 c
границей (p,u); А5 с гра-
ницей (o,p,r).
s
А3
A1
C
t
p
u
q
r
А4
А5
А2
о

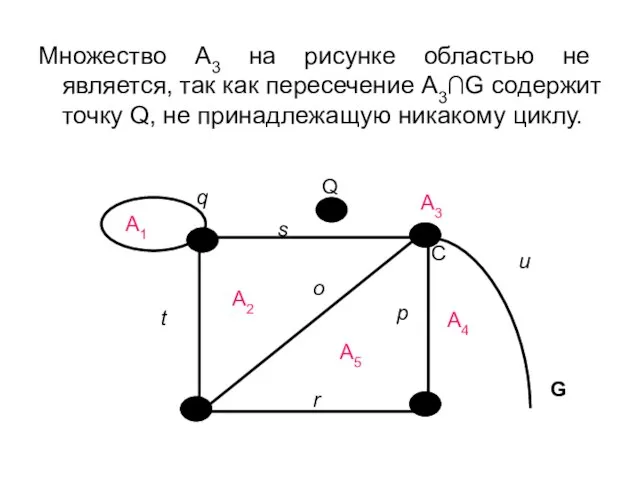
Множество А3 на рисунке областью не является, так как пересечение А3∩G содержит точку Q, не принадлежащую никакому циклу.
C
G

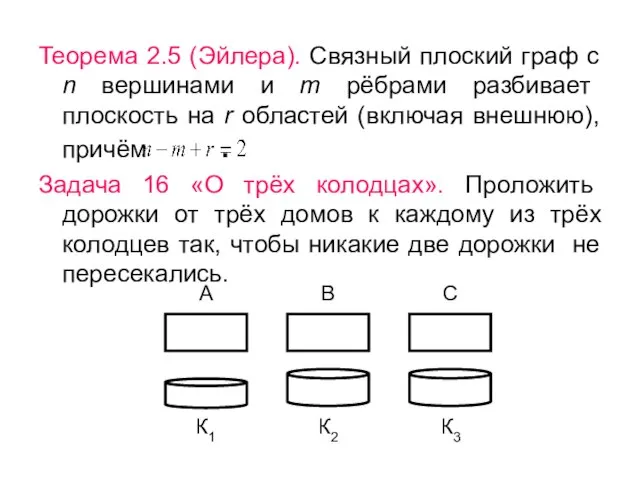
А
Теорема 2.5 (Эйлера). Связный плоский граф с n вершинами и m рёбрами разбивает плоскость на r областей (включая внешнюю), причём .
Задача 16 «О трёх колодцах». Проложить дорожки от трёх домов к каждому из трёх колодцев так, чтобы никакие две дорожки не пересекались.
К1
В
С
К2
К3

Решение.
Предположим, что эти 9 тропинок можно проложить.
Обозначим домики точками А, В, С, колодцы - точками К1, К2, К3. Каждую точку-дом соединим с каждой точкой-колодцем.
Получились ребра (графа) в количестве девяти штук, которые попарно не пересекаются.
Такие ребра образуют на рассматриваемой плоскости задачи многоугольник, поделенный на меньшие многоугольники.
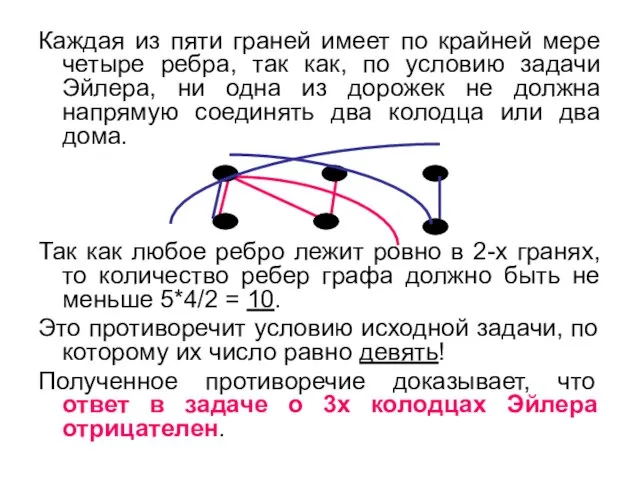
Для такого разбиения должно выполняться известное соотношение Эйлера п - т + r = 2, причем n = 6 и m = 9. Получается, r = 5.

Каждая из пяти граней имеет по крайней мере четыре ребра, так как, по условию задачи Эйлера, ни одна из дорожек не должна напрямую соединять два колодца или два дома.
Так как любое ребро лежит ровно в 2-х гранях, то количество ребер графа должно быть не меньше 5*4/2 = 10.
Это противоречит условию исходной задачи, по которому их число равно девять!
Полученное противоречие доказывает, что ответ в задаче о 3х колодцах Эйлера отрицателен.

Граф называется двудольным, если его вершины разбиты на два непересекающихся подмножества: , а рёбра связывают вершины только из разных классов (не обязательно все пары).
Если каждая вершина множества V1 связана ребром с каждой вершиной множества V2, то двудольный граф называется полным двудольным и обозначается , где .
Примером двудольного полного графа является граф к рассмотренной задаче, которую называют «Три дома – три колодца», показывая этим два непересекающихся множества вершин графа.

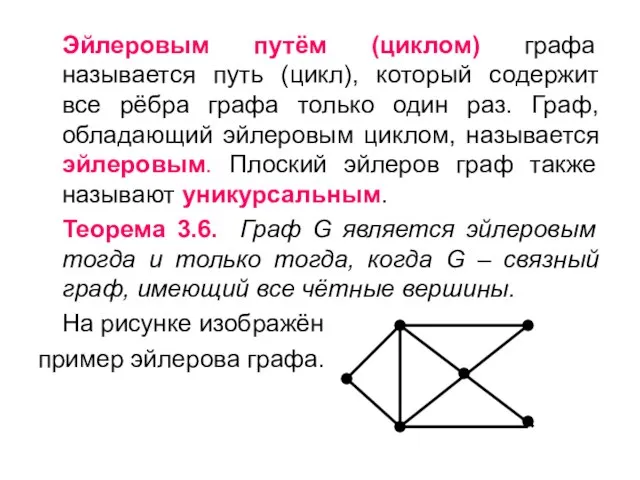
Эйлеровым путём (циклом) графа называется путь (цикл), который содержит все рёбра графа только один раз. Граф, обладающий эйлеровым циклом, называется эйлеровым. Плоский эйлеров граф также называют уникурсальным.
Теорема 3.6. Граф G является эйлеровым тогда и только тогда, когда G – связный граф, имеющий все чётные вершины.
На рисунке изображён
пример эйлерова графа.

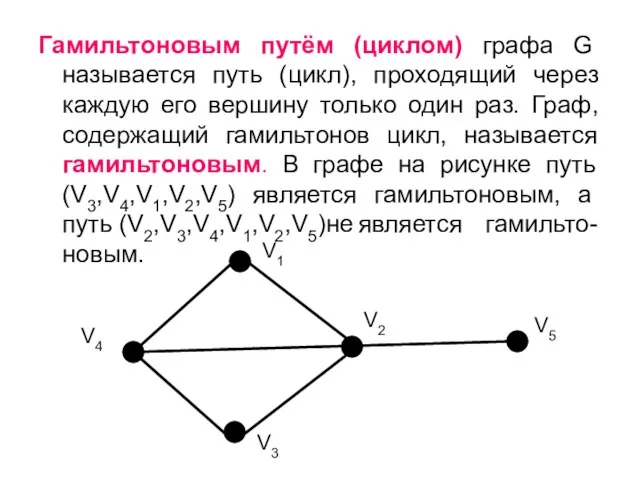
Гамильтоновым путём (циклом) графа G называется путь (цикл), проходящий через каждую его вершину только один раз. Граф, содержащий гамильтонов цикл, называется гамильтоновым. В графе на рисунке путь (V3,V4,V1,V2,V5) является гамильтоновым, а путь (V2,V3,V4,V1,V2,V5) не является гамильто-новым.
V4
V1
V2
V5
V3

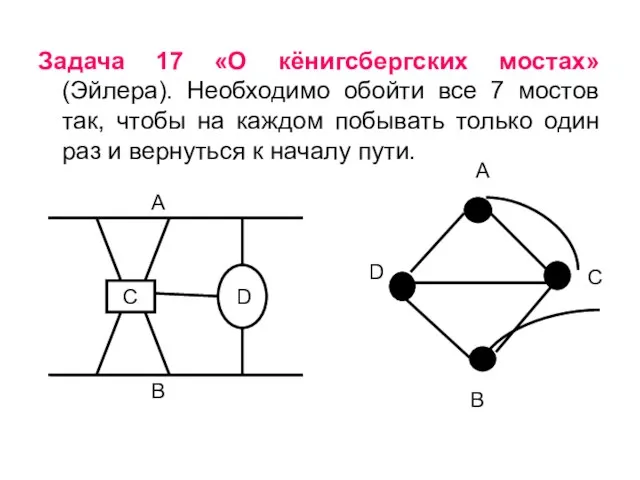
Задача 17 «О кёнигсбергских мостах» (Эйлера). Необходимо обойти все 7 мостов так, чтобы на каждом побывать только один раз и вернуться к началу пути.
С
D
A
B
A
D
B
С

Решение.
Представим задачу в виде графа, в котором острова и берега обозначим точками, т.е. они будут вершинами графа. Мосты будут рёбрами графа.
Поскольку необходимо пройти по всем мостам по одному разу и вернуться туда, откуда начали обход мостов, это значит, что нужно по всем рёбрам графа пройти по одному разу, т.е. образовать эйлеров цикл.
Следовательно, нужно проверить, является ли рассматриваемый граф эйлеровым.

Но в теореме 3.6. говорится о том, что для того чтобы граф был эйлеровым необходимо и достаточно, чтобы граф был связным, и все вершины были чётные, т.е. чтобы из каждой вершины исходило чётное количество рёбер.
Если посчитать рёбра, то увидим, что вершины А и В, которыми обозначены берега, имеют степень 3, следовательно, они нечётные.
Таким образом, условие теоремы не выполнено, значит ответ задачи отрицательный: невозможно обойти все мосты по одному разу и вернуться в исходную точку.

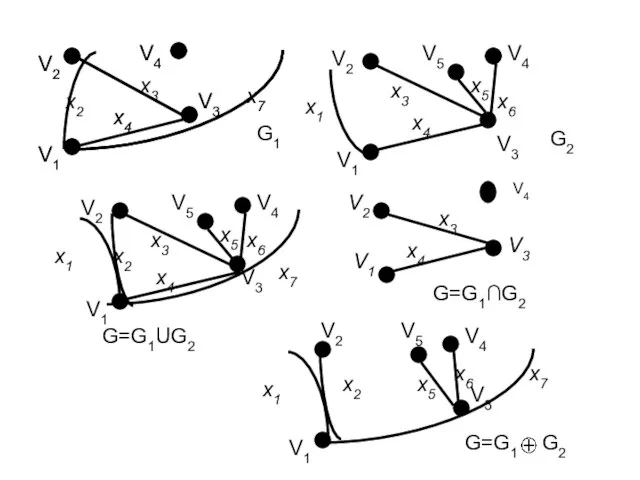
2.2. Операции над графами
Объединением графов и называется граф , множество вершин которого , а множество рёбер .
Пересечением графов и называется граф , для которого - множество рёбер, а - множество вершин.
Кольцевой суммой двух графов называется граф , порождённый множеством вершин и множеством рёбер , т.е. множеством рёбер, содержащихся либо в , либо в , но не в .

х3
х4
х6
G1
V2
V1
V3
V4
V5
х3
х1
х5
G=G1UG2
х6
х4
х4
х3
V3
V2
V1
G=G1∩G2
х2
х2
V2
V1
V3
V4
х7
V5
х1
G=G1 G2
V4
х7
х5
х6

Подграфом графа называется граф , все вершины и рёбра которого являются подмножествами множества вершин и рёбер графа G.
Компонентой связности неориенти-рованного графа называется его подграф с множеством вершин и множеством рёбер , инци-дентных только вершинам из множества , причём ни одна вершина из не смеж-на с вершинами из множества .

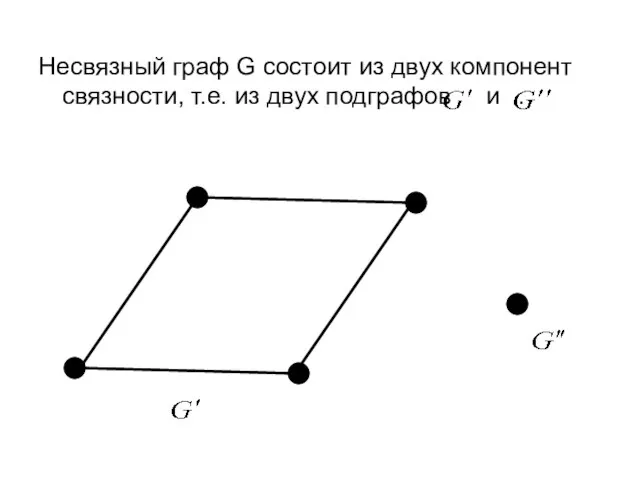
Несвязный граф G состоит из двух компонент связности, т.е. из двух подграфов и .

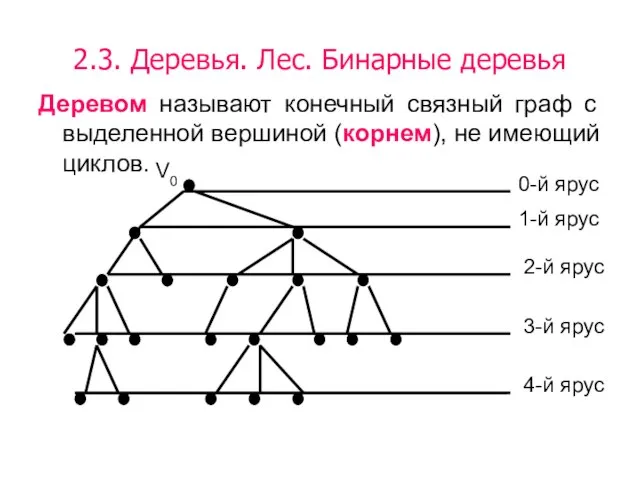
2.3. Деревья. Лес. Бинарные деревья
Деревом называют конечный связный граф с выделенной вершиной (корнем), не имеющий циклов.
0-й ярус
1-й ярус
2-й ярус
3-й ярус
4-й ярус
V0

Для каждой пары вершин дерева – узлов – существует единственный маршрут, поэтому вершины удобно классифицировать по степени удалённости от корневой вершины.
Расстояние до корневой вершины называется ярусом s вершины, .
Теорема 2.7. Граф является деревом тогда и только тогда, когда выполняется хотя бы одно из условий:
граф связен и не содержит циклов;
граф не содержит циклов и имеет n – 1 ребро;

граф связен и имеет п – 1 ребро;
граф не содержит циклов, но добавление ребра между несмежными вершинами приводит к появлению одного и только одного элементарного цикла;
граф связный, но утрачивает это свойство после удаления любого ребра;
в графе всякая пара вершин соединена цепью, и только одной.
Висячие вершины, за исключением корневой, называются листьями.

Упорядоченное объединение деревьев представляет собой несвязный граф, называемый лесом.
Остовом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.
Кодеревом остова Т графа G называется дополнение Т до G, т.е. такой его подграф, который содержит все его вершины и только те его рёбра, которые не входят в Т.

При описании деревьев принято использовать термины: отец, сын, предок, потомок.
Каждая вершина дерева называется узлом, причём каждый узел является корнем дерева, состоящего из поддеревьев. Узел k-го яруса называется отцом узла (k + 1)–го яруса, если они смежны. Узел (k + 1)–го яруса называется сыном узла k-го яруса. Два узла, имеющие одного отца, называются братьями.
Упорядоченным деревом называется дерево, в котором поддеревья каждого узла образуют упорядоченное подмножество.

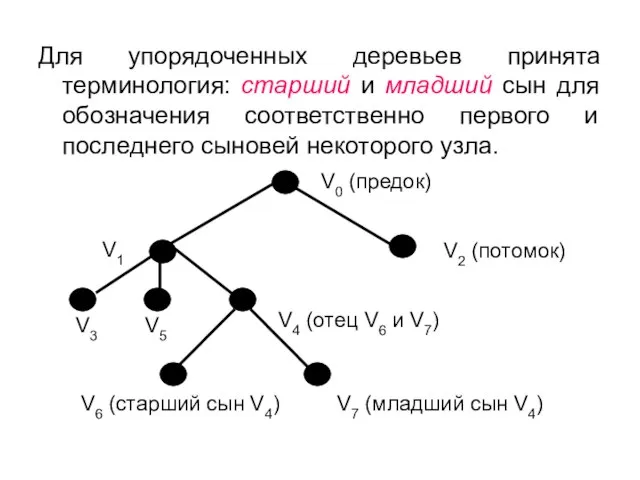
V3
V5
V1
Для упорядоченных деревьев принята терминология: старший и младший сын для обозначения соответственно первого и последнего сыновей некоторого узла.
V0 (предок)
V2 (потомок)
V4 (отец V6 и V7)
V6 (старший сын V4)
V7 (младший сын V4)

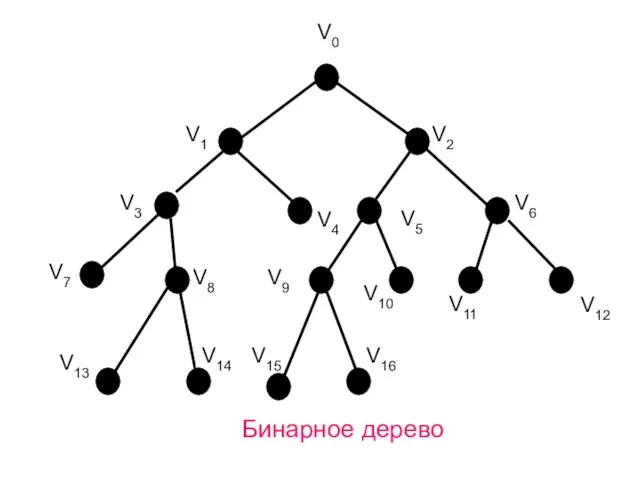
Деревья, в которых каждый узел либо является листом, либо образует два поддерева: левое и правое, называются бинарными деревьями и используются при делении множества на два взаимоисключающих подмножества по какому-то признаку (дихотомическое деление).
Бинарное дерево уровня n называется полным, если каждый его узел уровня n является листом, а каждый узел уровня меньше, чем n, имеет непустое левое и правое поддеревья.

V1
V10
V7
V15
V9
V0
V2
V4
V13
V3
V5
Бинарное дерево
V6
V8
V14
V11
V12
V16
V11

Цикломатическим числом неориентированного графа G называется число ,
где - число его рёбер;
- число связных компонент графа;
- число вершин.
Цикломатическое число показывает, сколько рёбер нужно удалить из графа, чтобы в нём не стало циклов.
Цикломатическое число графа

3.4. Способы задания графа.
Изоморфные графы
Геометрическое представление плоского графа называется его реализацией.
При переходе от алгебраического способа (способа задания графа дугами путём указания вершин, которым они инцидентны) к геометрическому одному и тому же графу могут соответствовать различные изображения – изоморфные графы.
Граф можно задавать таблицей, состоящей из n строк (вершины) и т столбцов (рёбра).
Одним из самых распространённых способов задания графа является матричный способ.

Матрицей инцидентности называется таблица В, состоящая из n строк (вершины) и т столбцов (рёбра), в которой:
для неориентированного графа:
, если вершина инцидентна ребру ;
, если вершина не инцидентна ребру ;
для ориентированного графа:
, если вершина является началом дуги ;
, если вершина не инцидентна дуге ;
, если вершина является концом дуги.

Матрицей смежности графа без кратных рёбер называется квадратная матрица А порядка n, в которой:
, если ;
, если .
При восстановлении графа по его матрице инцидентности можно получить граф лишь с точностью до изоморфизма.

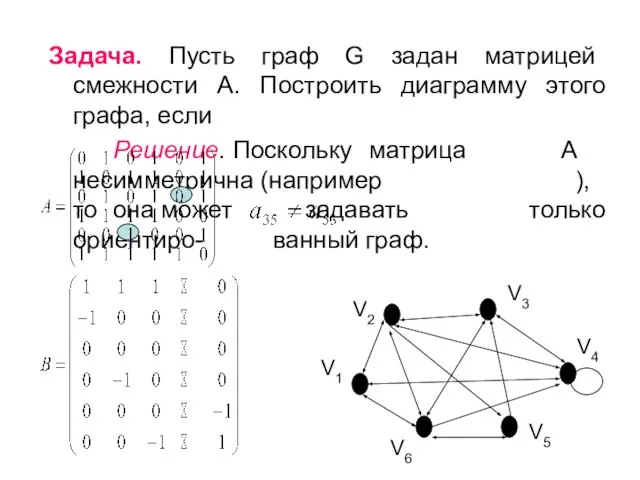
Задача. Пусть граф G задан матрицей смежности А. Построить диаграмму этого графа, если
Решение. Поскольку матрица А несимметрична (например ), то она может задавать только ориентиро- ванный граф.
V1
V2
V3
V4
V5
V6