Содержание
- 2. Эпиграф урока: «Число , место и комбинация – три взаимно перекрещивающиеся, но отличные сферы мышления, к
- 3. Задачи вводящие в комбинаторику. Задача 1. Дан квадрат 3х3. Распределить числа от 1 до 9 в
- 4. Что такое комбинаторика? Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных
- 5. Фигурные числа. В древности для облегчения вычислений часто использовали камешки. При этом особое внимание уделялось числу
- 6. Фигурные числа.
- 7. Квадратные числа
- 8. Магические и латинские квадраты.
- 9. 1. Посчитать число однобуквенных слов русского языка; 2. Записать первые двенадцать квадратных чисел; 3. Записать первые
- 10. Домашнее задание 1. Записать n- е по порядку кв. число, если: 1) n =20; 2) n
- 12. Скачать презентацию
Слайд 2Эпиграф урока:
«Число , место и комбинация – три взаимно перекрещивающиеся, но
Эпиграф урока:
«Число , место и комбинация – три взаимно перекрещивающиеся, но

отличные сферы мышления, к которым можно отнести все математические идеи».
Дж. Сильвестр
Дж. Сильвестр
Слайд 3Задачи вводящие в комбинаторику.
Задача 1. Дан квадрат 3х3. Распределить числа от 1
Задачи вводящие в комбинаторику.
Задача 1. Дан квадрат 3х3. Распределить числа от 1

до 9 в клетках квадрата так, чтобы сумма чисел по вертикалям. Горизонталям и
диагоналям равнялась бы 15.
Задача 2. Три друга- Антон, Борис и Виктор – приобрели два билета на футбольный матч. Сколько существует различных вариантов посещения футбольного матча для троих друзей?
Задача 3. Сколько различных трехзначных чисел можно составить из цифр 2, 3. 4 при условии, что а) цифры должны быть все различными; б) могут повторяться.
Задача 4. Имеются помидоры (п), огурцы (о) и лук (л). Сколько различных салатов можно приготовить, если в каждый из них должны входить в равных долях 2 различных вида овощей?
Записать все сочетания овощей в составленных салатах.
Задача 5. Игра «Детская комбинаторика». Комбинаторика.
диагоналям равнялась бы 15.
Задача 2. Три друга- Антон, Борис и Виктор – приобрели два билета на футбольный матч. Сколько существует различных вариантов посещения футбольного матча для троих друзей?
Задача 3. Сколько различных трехзначных чисел можно составить из цифр 2, 3. 4 при условии, что а) цифры должны быть все различными; б) могут повторяться.
Задача 4. Имеются помидоры (п), огурцы (о) и лук (л). Сколько различных салатов можно приготовить, если в каждый из них должны входить в равных долях 2 различных вида овощей?
Записать все сочетания овощей в составленных салатах.
Задача 5. Игра «Детская комбинаторика». Комбинаторика.
Слайд 4Что такое комбинаторика?
Комбинаторика – это раздел математики, в котором изучаются вопросы
Что такое комбинаторика?
Комбинаторика – это раздел математики, в котором изучаются вопросы

о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Выбором объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например конструктору, разрабатывающему новую модель механизма, ученому-агроному, планирующему распределение с/х культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав.
С комбинаторными задачами люди столкнулись в глубокой древности. В Древнем Китае увлекались составлением магических квадратов. В Древней Греции занимались теорией фигурных чисел.
Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. Комбинаторика становится наукой лишь в 18 в. – в период, когда возникла теория вероятности.
После первых работ, выполненных в 16в. Итальянскими учеными Дж.Кардано, Н.Тартальей и Г.Галилеем, такие задачи изучали французские математики Б.паскаль и П.Ферма. Первым рассмотрел комбинаторику как самостоятельная ветвь науки немецкий философ и математик Г.Лейбниц, опубликовавший в 1666г. Работу «Об искусстве комбинаторики». Замечательные достижения в области комбинаторики принадлежат Л.Эймеру.
Выбором объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например конструктору, разрабатывающему новую модель механизма, ученому-агроному, планирующему распределение с/х культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав.
С комбинаторными задачами люди столкнулись в глубокой древности. В Древнем Китае увлекались составлением магических квадратов. В Древней Греции занимались теорией фигурных чисел.
Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. Комбинаторика становится наукой лишь в 18 в. – в период, когда возникла теория вероятности.
После первых работ, выполненных в 16в. Итальянскими учеными Дж.Кардано, Н.Тартальей и Г.Галилеем, такие задачи изучали французские математики Б.паскаль и П.Ферма. Первым рассмотрел комбинаторику как самостоятельная ветвь науки немецкий философ и математик Г.Лейбниц, опубликовавший в 1666г. Работу «Об искусстве комбинаторики». Замечательные достижения в области комбинаторики принадлежат Л.Эймеру.
Слайд 5Фигурные числа.
В древности для облегчения вычислений часто использовали камешки. При этом
Фигурные числа.
В древности для облегчения вычислений часто использовали камешки. При этом

особое внимание уделялось числу камешков, которые можно было разложить в виде правильной фигуры. Так появились квадратные числа, сконструированы треугольные и пятиугольные числа.
Квадратное число находится по формуле:
Nкв.=п х п
Треугольное число находится по формуле:
Nтр.=п(п-1):2
Пятиугольные числа находятся по формуле:
Nпят.=п+3п(п-1):2
Все составные числа древние математики представляли в виде прямоугольников.
Квадратное число находится по формуле:
Nкв.=п х п
Треугольное число находится по формуле:
Nтр.=п(п-1):2
Пятиугольные числа находятся по формуле:
Nпят.=п+3п(п-1):2
Все составные числа древние математики представляли в виде прямоугольников.
Слайд 6Фигурные числа.
Фигурные числа.

Слайд 7Квадратные числа
Квадратные числа

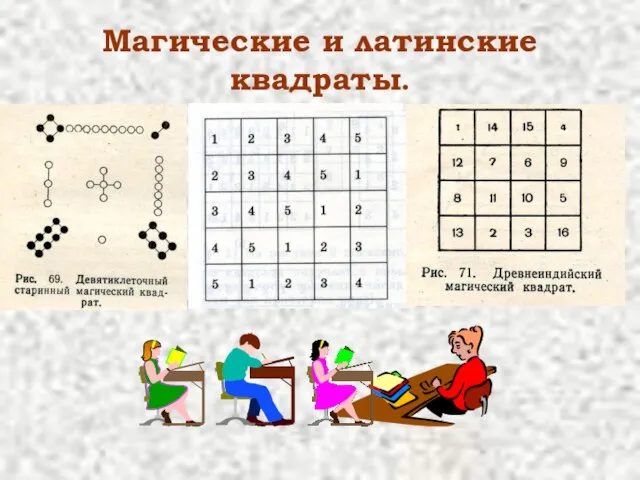
Слайд 8Магические и латинские квадраты.
Магические и латинские квадраты.
Слайд 9
1. Посчитать число однобуквенных слов русского языка;
2. Записать первые
1. Посчитать число однобуквенных слов русского языка;
2. Записать первые

двенадцать квадратных чисел;
3. Записать первые десять треугольных чисел;
4. Составить латинский квадрат.
Самостоятельная работа
Слайд 10Домашнее задание
1. Записать n- е по порядку кв. число, если:
1)
Домашнее задание
1. Записать n- е по порядку кв. число, если:
1)

n =20; 2) n =25 3) n =31;
2. Записать n- е по порядку треугольное число,
если: 1) n=20; 2) n=33; 3) n=34;
3. Изобразить в древних традициях всеми возможными
способами составное число: 1) 6; 2) 8; 3) 18; 4) 20;
4. Продолжить построение магического квадрата:
2. Записать n- е по порядку треугольное число,
если: 1) n=20; 2) n=33; 3) n=34;
3. Изобразить в древних традициях всеми возможными
способами составное число: 1) 6; 2) 8; 3) 18; 4) 20;
4. Продолжить построение магического квадрата:
 Пиломатериалы, получение и применение
Пиломатериалы, получение и применение Совместное использование пакета Microsoft Office Excel 2007 и служб интеллектуального анализа данных SQL Server Analysis Services
Совместное использование пакета Microsoft Office Excel 2007 и служб интеллектуального анализа данных SQL Server Analysis Services Управление качеством
Управление качеством Стиль модерн и сопряжение
Стиль модерн и сопряжение «Удивительный мир многогранников»
«Удивительный мир многогранников» Промышленная Группа СОЮЗ. Многопрофильный холдинг, производитель полного спектра мебельных комплектующих для сборки мебели
Промышленная Группа СОЮЗ. Многопрофильный холдинг, производитель полного спектра мебельных комплектующих для сборки мебели Автономные энергетические системы на базе нетрадиционных источников энергии для горных поселений КР
Автономные энергетические системы на базе нетрадиционных источников энергии для горных поселений КР Модели и технологии обучения персонала розницы в период изменений
Модели и технологии обучения персонала розницы в период изменений Чрезвычайные ситуации техногенного характера
Чрезвычайные ситуации техногенного характера Тема проповеди: Виденье церковное – мое виденье
Тема проповеди: Виденье церковное – мое виденье Из конфликта в эффективную коммуникацию
Из конфликта в эффективную коммуникацию Политические режимы. Урок 3
Политические режимы. Урок 3 Зрительное восприятие цвета
Зрительное восприятие цвета Стратегия развития современных технологий мобильной связи на Дальнем Востоке и в Восточной Сибири
Стратегия развития современных технологий мобильной связи на Дальнем Востоке и в Восточной Сибири Сачки и дезертиры
Сачки и дезертиры Художественные образы СПБ: российский город на перекрёстке мировых культур
Художественные образы СПБ: российский город на перекрёстке мировых культур Фактори забезпечення конкурентоспроможності підприємства
Фактори забезпечення конкурентоспроможності підприємства Три клада у Природы есть:вода,Земля и воздух – три ее основы.Какая бы ни грянула беда,Целы они – все возродится снова.
Три клада у Природы есть:вода,Земля и воздух – три ее основы.Какая бы ни грянула беда,Целы они – все возродится снова. Конвейер проектов. Критерии и роли. Специфика выполнения
Конвейер проектов. Критерии и роли. Специфика выполнения Проектно-изыскательские работы. Градостроительная документация. Лекция 1
Проектно-изыскательские работы. Градостроительная документация. Лекция 1 Добыча нефти
Добыча нефти Презентация на тему Правописание падежных окончаний имен существительных единственного числа (4 класс)
Презентация на тему Правописание падежных окончаний имен существительных единственного числа (4 класс) THE PRESENT PERFECT TENSE НАСТОЯЩЕЕ СОВЕРШЕННОЕ ВРЕМЯ
THE PRESENT PERFECT TENSE НАСТОЯЩЕЕ СОВЕРШЕННОЕ ВРЕМЯ Кобелев Н.Б.ВЗФЭИ, Москва
Кобелев Н.Б.ВЗФЭИ, Москва Театрально-игровая деятельность - как средство развития творческих способностей детей дошкольного возраста
Театрально-игровая деятельность - как средство развития творческих способностей детей дошкольного возраста Презентация на тему Частица как служебная часть речи.
Презентация на тему Частица как служебная часть речи.  Спасенный сад
Спасенный сад Караоке-баттл 99 баллов. Описание игры
Караоке-баттл 99 баллов. Описание игры