Тема урока: Вычисление расстояния от точки до плоскости

Колесова Ж. В.
1. Дайте определение прямой перпендикулярной плоскости.
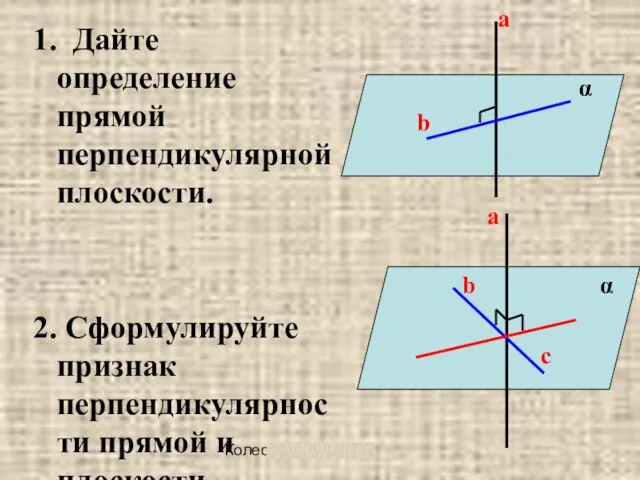
2. Сформулируйте признак перпендикулярности прямой и плоскости.
а
b α
c
а
α
b

Колесова Ж. В.
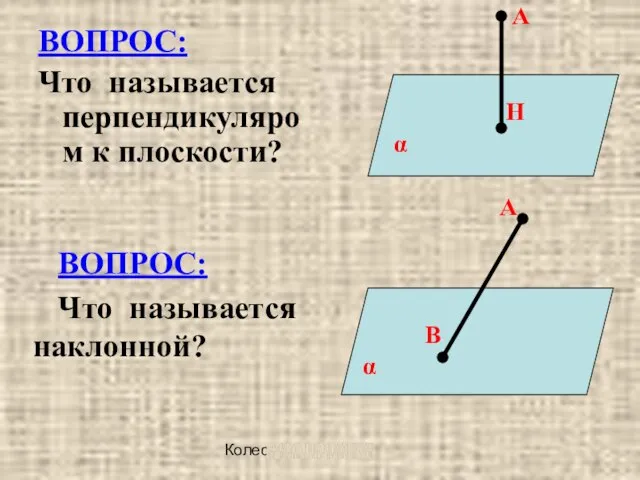
ВОПРОС:
Что называется перпендикуляром к плоскости?
А
Н
α
А
В
α

Колесова Ж. В.
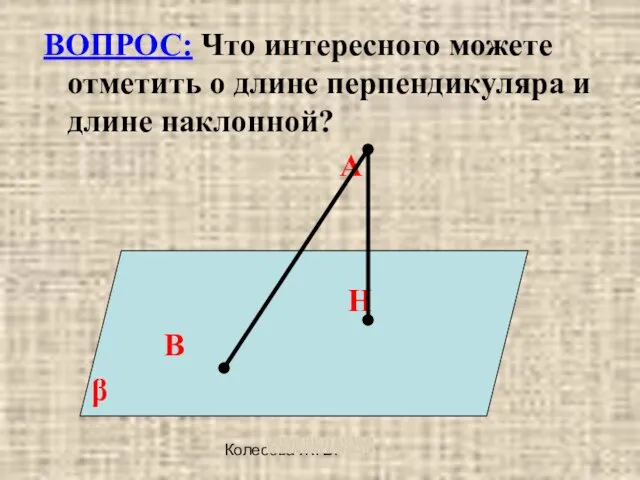
ВОПРОС: Что интересного можете отметить о длине перпендикуляра и длине наклонной?
А
Н
В
β

Колесова Ж. В.
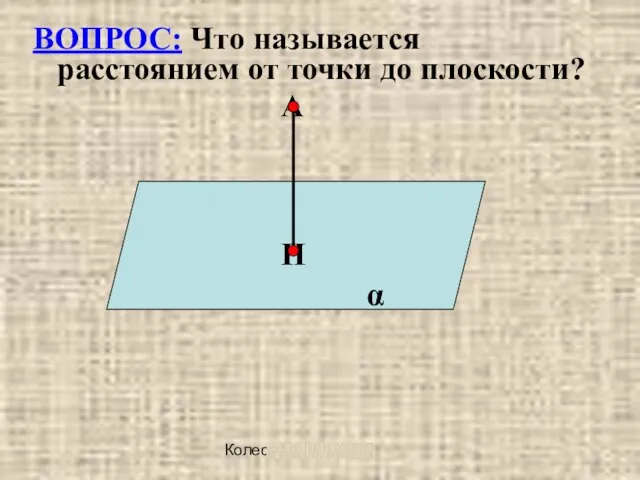
ВОПРОС: Что называется расстоянием от точки до плоскости?
А
Н

Колесова Ж. В.
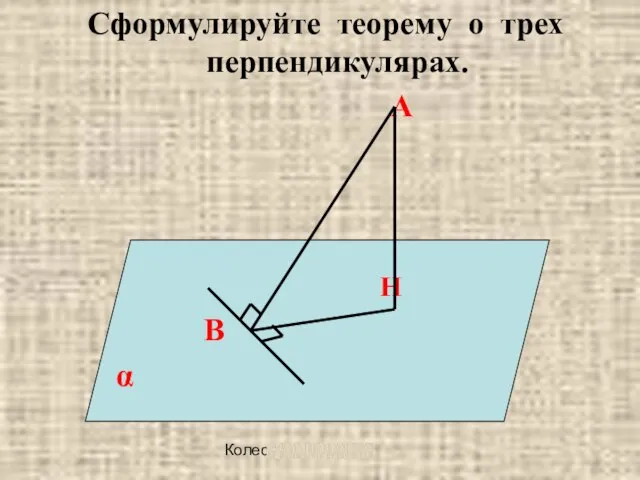
Сформулируйте теорему о трех перпендикулярах.
А
Н
В
α

Колесова Ж. В.
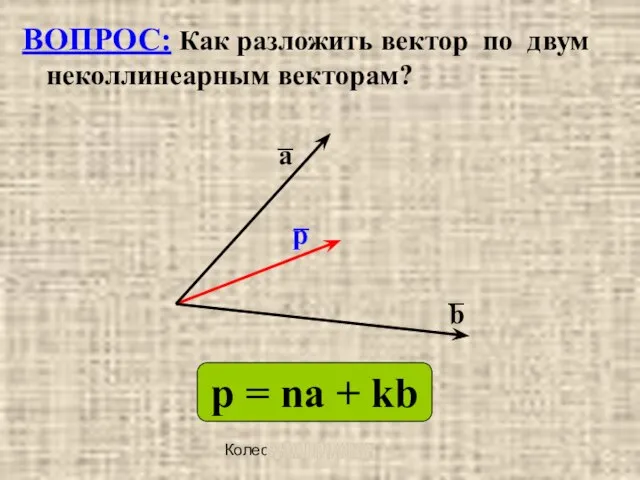
ВОПРОС: Как разложить вектор по двум неколлинеарным векторам?
а
р
b

Колесова Ж. В.
A
b c
r
M
C
a B
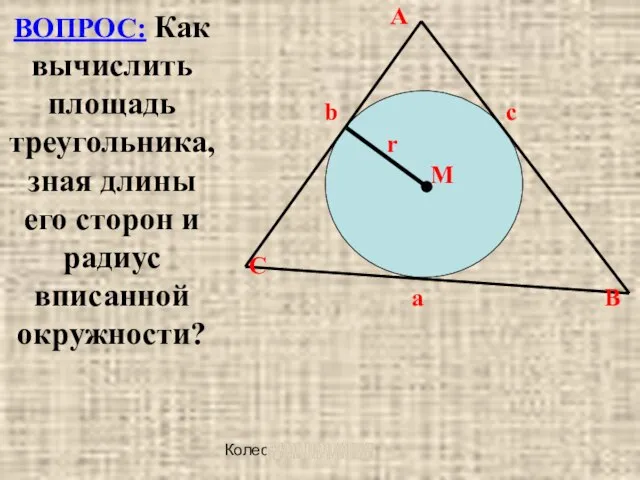
ВОПРОС: Как вычислить площадь треугольника, зная длины его сторон и радиус вписанной окружности?

Колесова Ж. В.
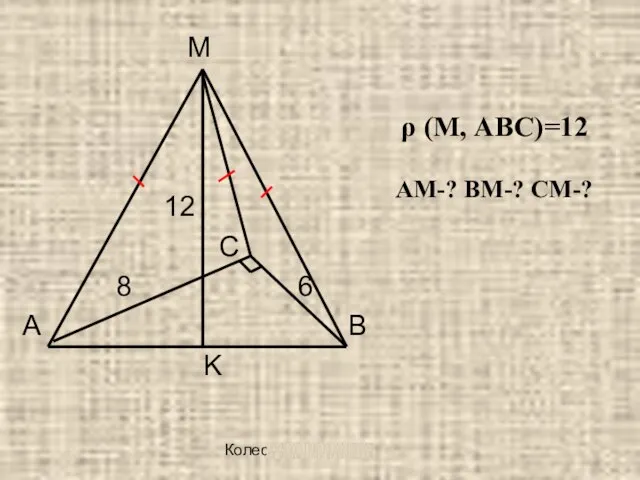
М
ρ (М, АВС)=12
12
С
8 6
А В K
АМ-? ВМ-? СМ-?

Колесова Ж. В.
М
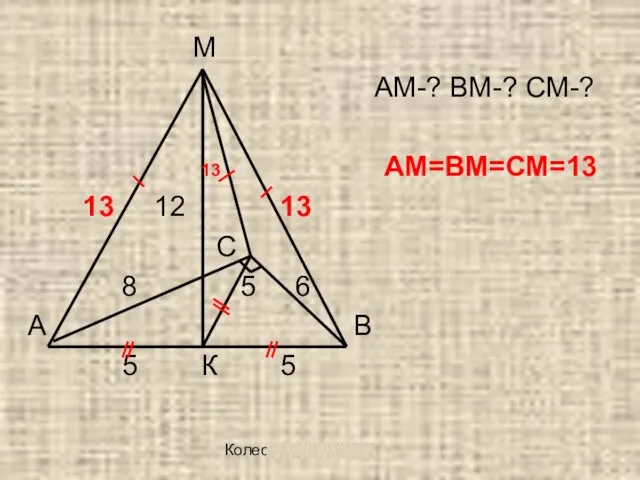
АМ-? ВМ-? СМ-?
13 АМ=ВМ=СМ=13
13 12 13 С
8 5 6
А В
5 К 5

Колесова Ж. В.
В
13 12
β
C
D а
ВС ┴ β
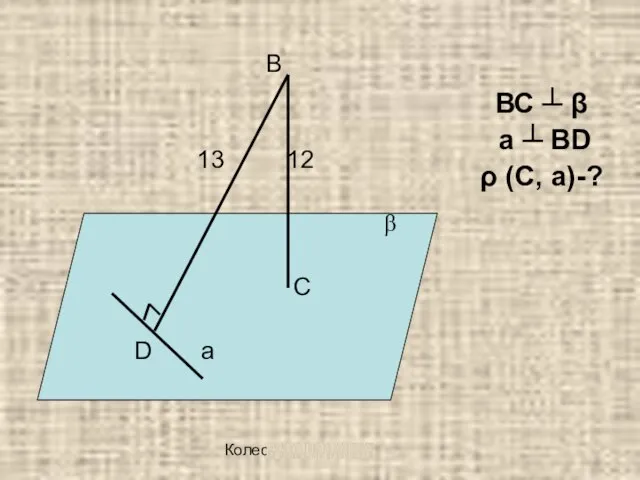
а ┴ BD
ρ (C, а)-?

Колесова Ж. В.
В
13 12
β
5 C
D а
ВС ┴ β
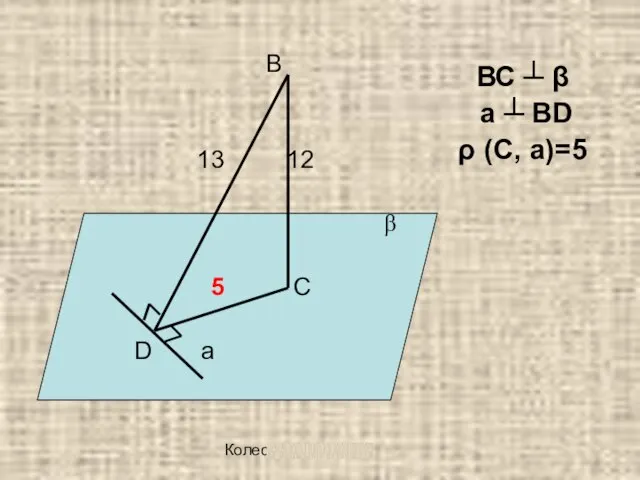
а ┴ BD
ρ (C, а)=5

Колесова Ж. В.
S
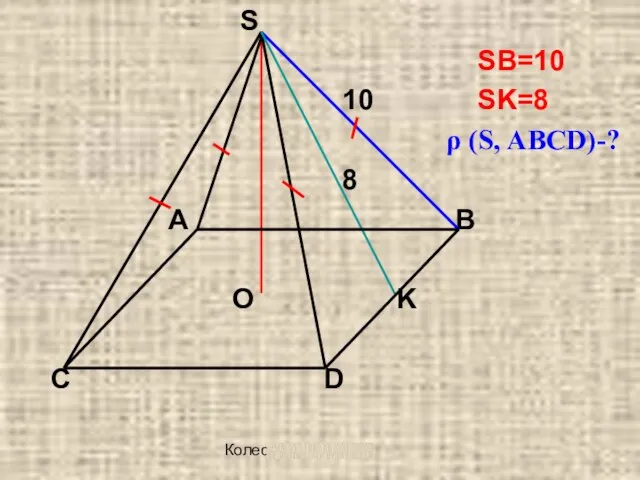
SB=10
10 SK=8
ρ (S, ABCD)-?
8
A B
O K
C D

Колесова Ж. В.
S
SB=10
10 SK=8
ρ (S, ABCD)-?
8
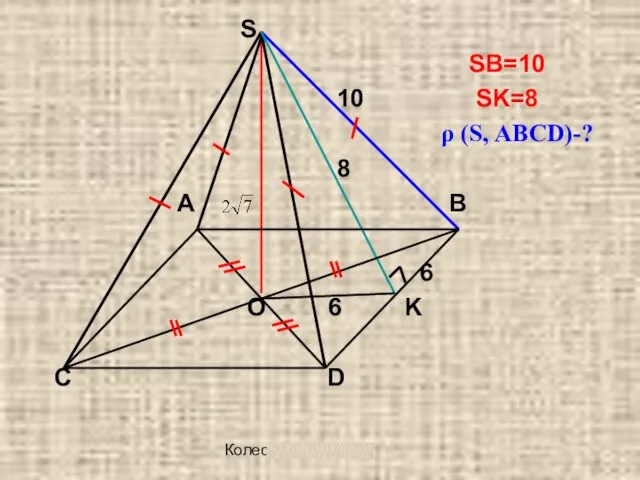
A B
6
O 6 K
C D

Колесова Ж. В.
ЗАДАЧА
Даны две параллельные плоскости и множество треугольников, таких, что в каждом треугольнике две вершины принадлежат первой из двух данных плоскостей, а третья вершина — второй. Какую фигуру образует множество всех точек пересечения медиан треугольников?