Презентация на тему Теорема Менелая и теорема Чевы

Содержание
Теоретические основы
Теорема Чевы
Теорема Менелая
Методические рекомендации
Методика обучения решению задач в период предпрофильной подготовки
Изучение темы «Теорема Менелая и теорема Чевы» в курсе геометрии 10 классаИзучение темы «Теорема Менелая и теорема Чевы» в курсе геометрии 10 класса Изучение темы «Теорема Менелая и теорема Чевы» в курсе геометрии 10 класса
Применение теорем Менелая и Чевы в решении стереометрических задач

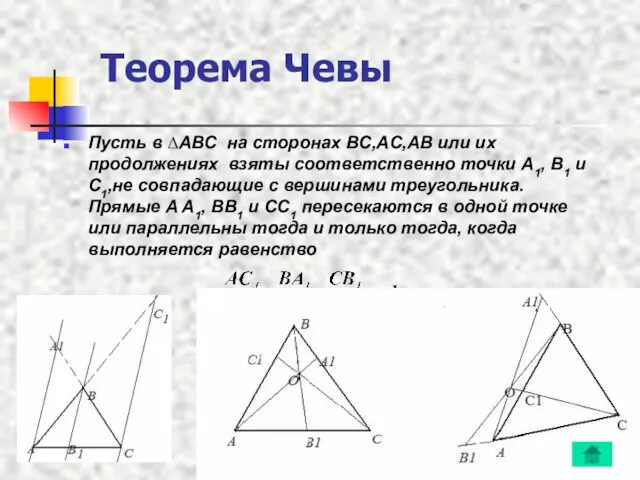
Теорема Чевы
Пусть в ∆ABC на сторонах BC,AC,AB или их продолжениях взяты соответственно точки A1, B1 и C1,не совпадающие с вершинами треугольника. Прямые A A1, BB1 и CC1 пересекаются в одной точке или параллельны тогда и только тогда, когда выполняется равенство

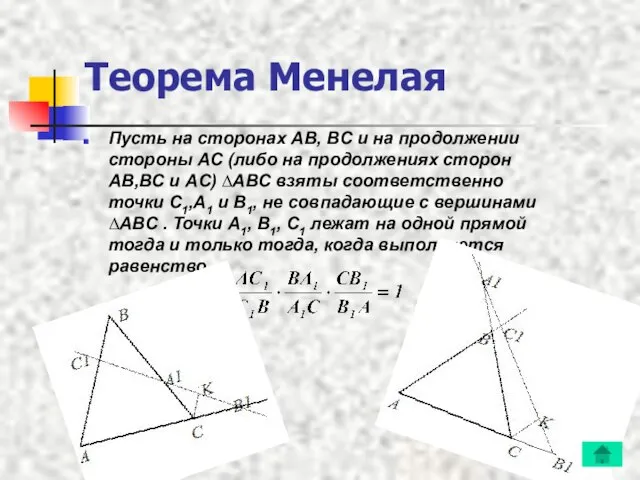
Теорема Менелая
Пусть на сторонах AB, BC и на продолжении стороны AC (либо на продолжениях сторон AB,BC и AC) ∆ABC взяты соответственно точки C1,A1 и B1, не совпадающие с вершинами ∆ABC . Точки A1, B1, C1 лежат на одной прямой тогда и только тогда, когда выполняется равенство

Методика обучения решению задач в период предпрофильной подготовки
1. Теорема Менелая и пропорциональные отрезки в треугольнике.
2. Теорема Чевы и ее следствия. Применение теорем Чевы и Менелая к задачам на доказательство.
3. Решение задач на пропорциональное деление отрезков в треугольнике.
4. Решение задач, связанных с нахождением площадей.
5. Комбинированные задачи.

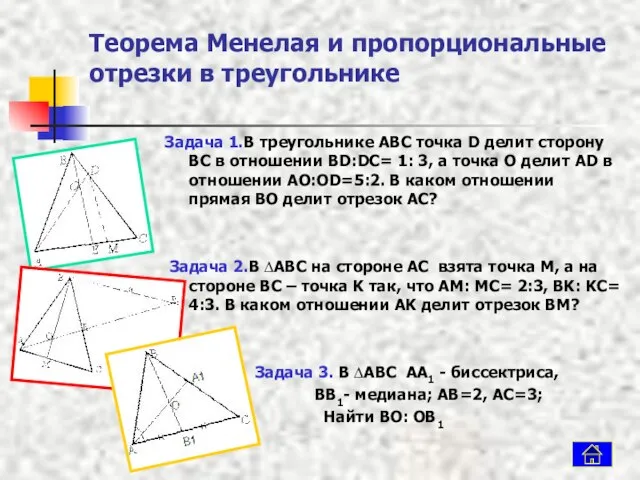
Теорема Менелая и пропорциональные отрезки в треугольнике
Задача 1.В треугольнике ABC точка D делит сторону BC в отношении BD:DC= 1: 3, а точка O делит AD в отношении AO:OD=5:2. В каком отношении прямая BO делит отрезок AC?
Задача 2.В ∆ABC на стороне AC взята точка M, а на стороне BC – точка K так, что AM: MC= 2:3, BK: KC= 4:3. В каком отношении AK делит отрезок BM?
Задача 3. В ∆ABC AA1 - биссектриса,
BB1- медиана; AB=2, AC=3;
Найти BO: OB1

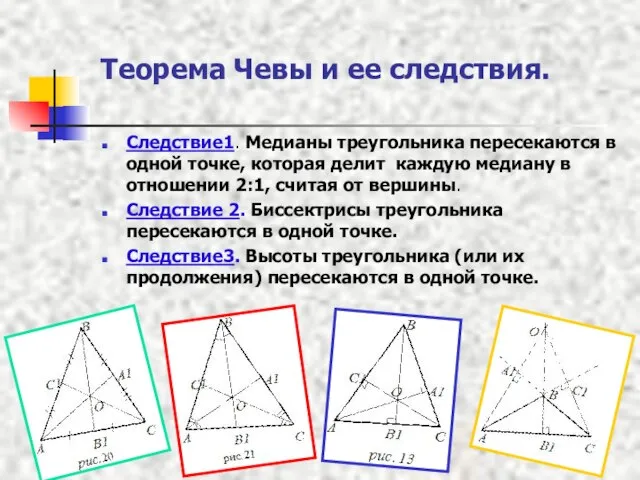
Теорема Чевы и ее следствия.
Следствие1. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Следствие 2. Биссектрисы треугольника пересекаются в одной точке.
Следствие3. Высоты треугольника (или их продолжения) пересекаются в одной точке.

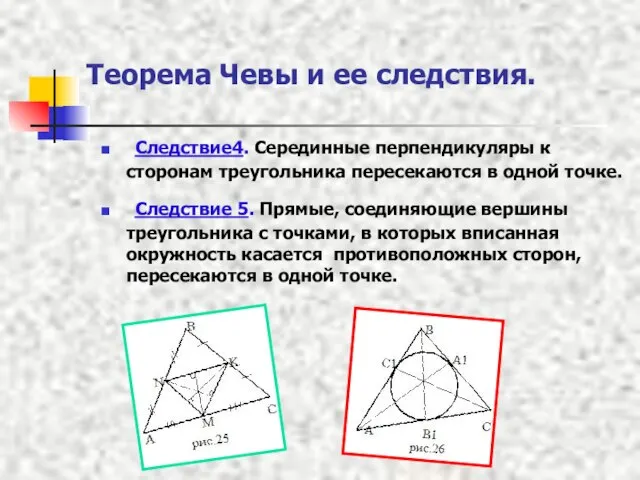
Теорема Чевы и ее следствия.
Следствие4. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Следствие 5. Прямые, соединяющие вершины треугольника с точками, в которых вписанная окружность касается противоположных сторон, пересекаются в одной точке.

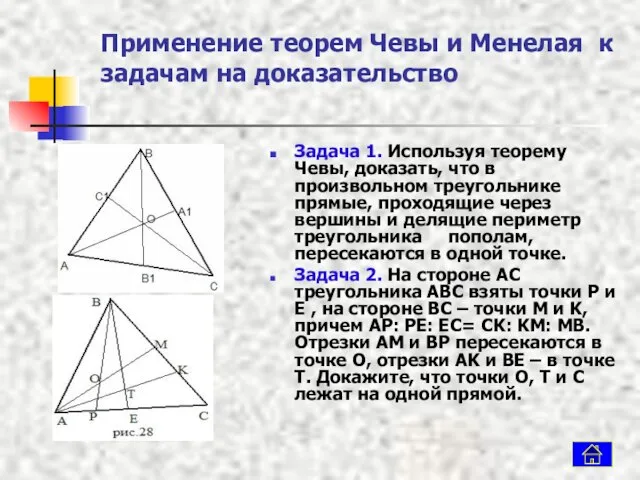
Применение теорем Чевы и Менелая к задачам на доказательство
Задача 1. Используя теорему Чевы, доказать, что в произвольном треугольнике прямые, проходящие через вершины и делящие периметр треугольника пополам, пересекаются в одной точке.
Задача 2. На стороне AC треугольника ABC взяты точки P и E , на стороне BC – точки M и K, причем AP: PE: EC= CK: KM: MB. Отрезки AM и BP пересекаются в точке O, отрезки AK и BE – в точке T. Докажите, что точки O, T и С лежат на одной прямой.

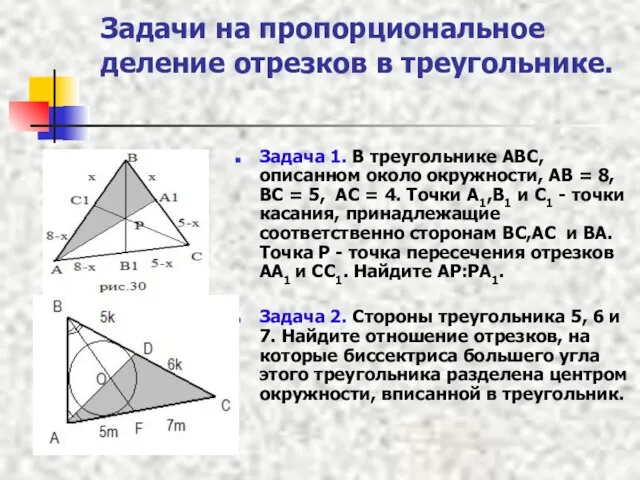
Задачи на пропорциональное деление отрезков в треугольнике.
Задача 1. В треугольнике ABC, описанном около окружности, AB = 8, BC = 5, AC = 4. Точки A1,В1 и C1 - точки касания, принадлежащие соответственно сторонам BC,AC и BA. Точка P - точка пересечения отрезков AA1 и CC1. Найдите AP:PA1.
Задача 2. Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.

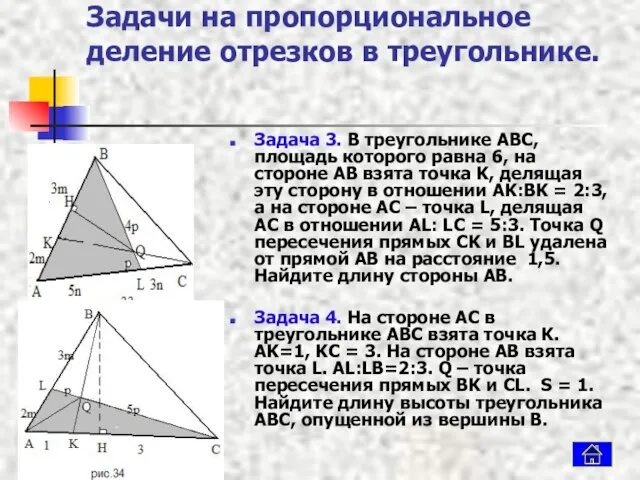
Задачи на пропорциональное деление отрезков в треугольнике.
Задача 3. В треугольнике ABC, площадь которого равна 6, на стороне AB взята точка K, делящая эту сторону в отношении AK:BK = 2:3, а на стороне AC – точка L, делящая AC в отношении AL: LC = 5:3. Точка Q пересечения прямых CK и BL удалена от прямой AB на расстояние 1,5. Найдите длину стороны AB.
Задача 4. На стороне AC в треугольнике ABC взята точка K. AK=1, KC = 3. На стороне AB взята точка L. AL:LB=2:3. Q – точка пересечения прямых BK и CL. S = 1. Найдите длину высоты треугольника ABC, опущенной из вершины B.

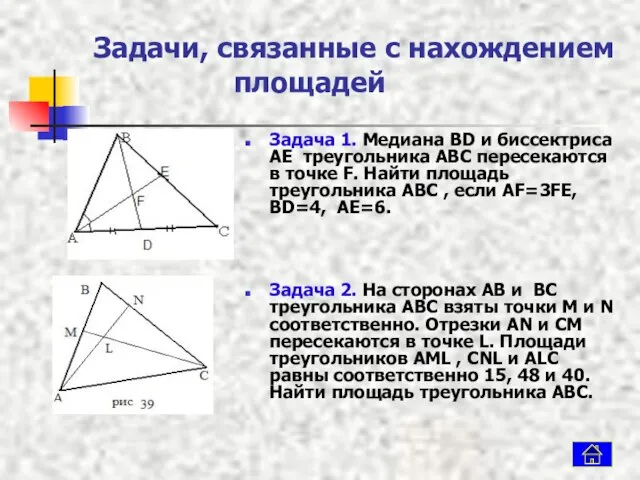
Задачи, связанные с нахождением
площадей
Задача 1. Медиана BD и биссектриса AE треугольника ABC пересекаются в точке F. Найти площадь треугольника ABC , если AF=3FE, BD=4, AE=6.
Задача 2. На сторонах AB и BC треугольника ABC взяты точки M и N соответственно. Отрезки AN и CM пересекаются в точке L. Площади треугольников AML , CNL и ALC равны соответственно 15, 48 и 40. Найти площадь треугольника ABC.

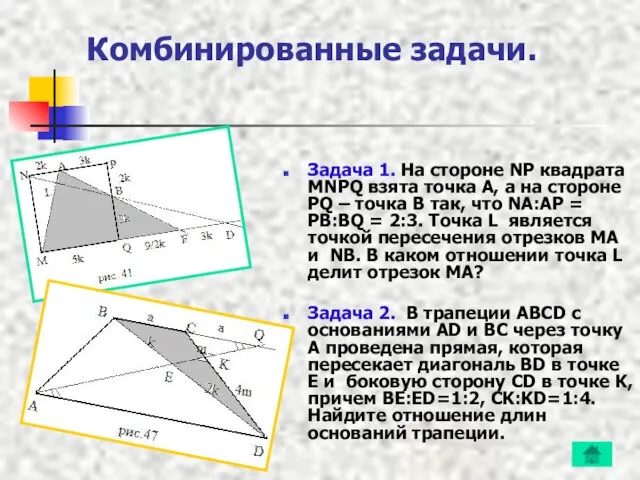
Комбинированные задачи.
Задача 1. На стороне NP квадрата MNPQ взята точка A, а на стороне PQ – точка B так, что NA:AP = PB:BQ = 2:3. Точка L является точкой пересечения отрезков MA и NB. В каком отношении точка L делит отрезок MA?
Задача 2. В трапеции ABCD с основаниями AD и BC через точку A проведена прямая, которая пересекает диагональ BD в точке E и боковую сторону CD в точке K, причем BE:ED=1:2, CK:KD=1:4. Найдите отношение длин оснований трапеции.

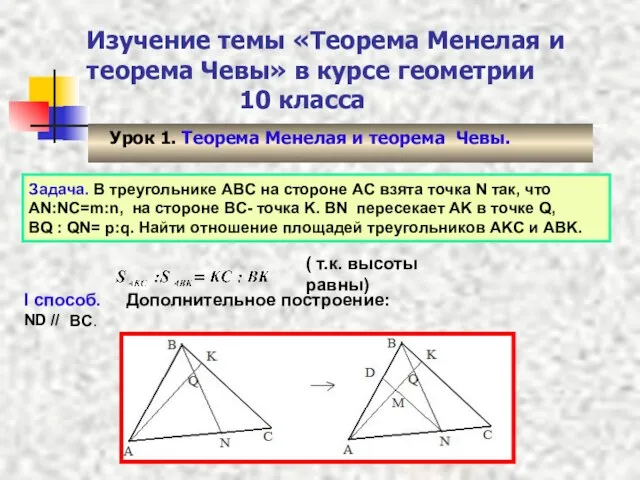
Изучение темы «Теорема Менелая и теорема Чевы» в курсе геометрии 10 класса Урок 1. Теорема Менелая и теорема Чевы.
Задача. В треугольнике ABC на стороне AC взята точка N так, что AN:NC=m:n, на стороне BC- точка K. BN пересекает AK в точке Q,
BQ : QN= p:q. Найти отношение площадей треугольников AKC и ABK.
( т.к. высоты равны)
I способ. Дополнительное построение: ND //
BC.

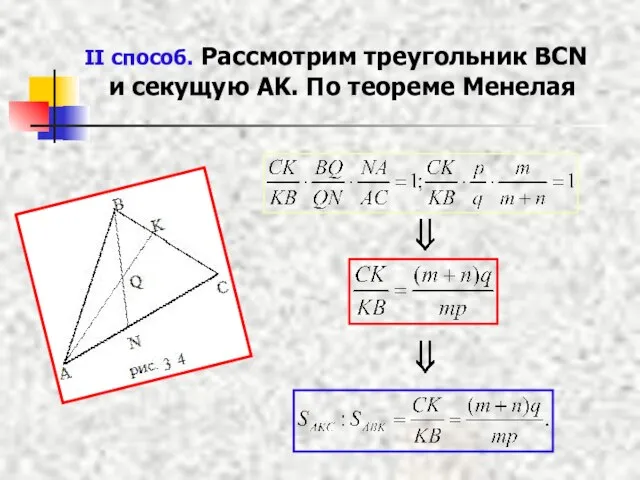
II способ. Рассмотрим треугольник BCN и секущую AK. По теореме Менелая

Урок 2. Применение теорем Менелая и Чевы в решении ключевых задач
Изучение темы «Теорема Менелая
и теорема Чевы» в курсе геометрии 10 класса
Цели урока: 1) формировать умения:
-видеть конфигурации, удовлетворяющие
заданным условиям;
-решать задачи нестандартными
способами;
-использовать теоремы в задачах на
доказательство;
2) развивать самостоятельность.

Задача. В равнобедренном треугольнике ABC (AС=BC) проведены медиана BN и высота АМ, которые пересекаются в точке D. AD=5, DM=2. Найти
Решение: AN=NC, AM=5+2=7. Рассмотрим ∆AMC и секущую NB. По теореме Менелая
Пусть коэффициент пропорциональности равен k, тогда СМ=3k, BM=2k. Из ∆ACM- прямоугольного:
;
,
,
Ответ:

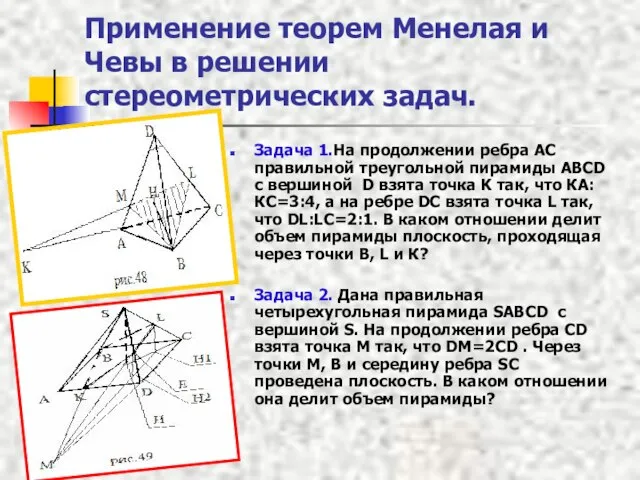
Применение теорем Менелая и Чевы в решении стереометрических задач.
Задача 1.На продолжении ребра АС правильной треугольной пирамиды ABCD с вершиной D взята точка K так, что КА:КС=3:4, а на ребре DC взята точка L так, что DL:LC=2:1. В каком отношении делит объем пирамиды плоскость, проходящая через точки B, L и К?
Задача 2. Дана правильная четырехугольная пирамида SABCD с вершиной S. На продолжении ребра CD взята точка M так, что DM=2CD . Через точки М, В и середину ребра SC проведена плоскость. В каком отношении она делит объем пирамиды?

Применение теорем Менелая и Чевы в решении стереометрических задач.
Задача 3. Дана правильная треугольная призма с боковыми ребрами AA1,BB1 и CC1. Причем на продолжении ребра BA взята точка M так, что MA=AB. Через точки M,B1 и середину ребра AC проведена плоскость. В каком отношении она делит объем призмы?