Теорема Пифагора

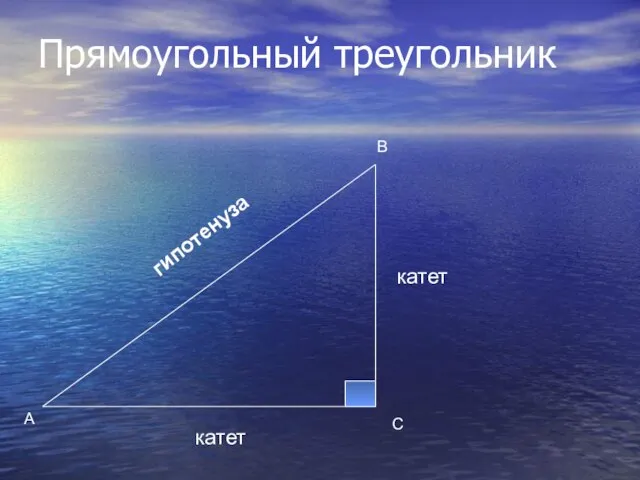
Прямоугольный треугольник
В
А
С
гипотенуза
катет
катет

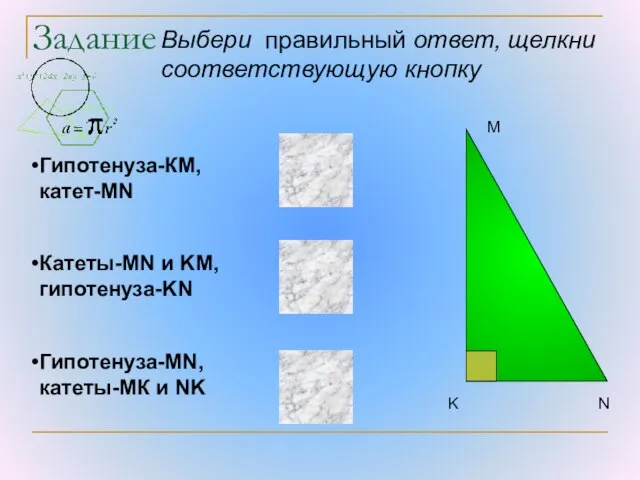
Выбери правильный ответ, щелкни соответствующую кнопку
K
M
N
Гипотенуза-КМ, катет-МN
Катеты-MN и KM, гипотенуза-KN
Гипотенуза-MN, катеты-МК и NK
Задание

Молодец! Пойдем дальше!
Интересна история теоремы Пифагора. Хотя она и связана с именем Пифагора, но была известна еще за 1200 лет до Пифагора, в вавилонских текстах. Возможно, Пифагор нашел доказательство соотношения между гипотенузой и катетами прямоугольного треугольника, которое до него было установлено опытным путем на основе измерений. В древнем предании говорится, что в честь своего открытия Пифагор принес в жертву богам быка, по другим свидетельствам – даже сто быков. Многие известные мыслители и писатели прошлого обращались к этой замечательной теореме и посвятили ей свои строки.
А сейчас говорят, что если человек не знает теорему Пифагора, то он не заботится о своей чести…

Немного о площади…
Площадь параллелограмма равна произведению его основания на высоту
Площадь треугольника равна половине произведения его основания на высоту
Площадь трапеции равна произведению полусуммы ее оснований на высоту

ТЕОРЕМА ПИФАГОРА
В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ КВАДРАТ ГИПОТЕНУЗЫ РАВЕН СУММЕ КВАДРАТОВ КАТЕТОВ
а
в
с
назад
вперед

КВАДРАТ, ПОСТРОЕННЫЙ НА ГИПОТЕНУЗЕ ДАННОГО ТРЕУГОЛЬНИКА, ПО ПЛОЩАДИ РАВЕН СУММЕ ПЛОЩАДЕЙ ДВУХ КВАДРАТОВ, ПОСТРОЕННЫХ НА КАТЕТАХ ДАННОГО ТРЕУГОЛЬНИКА.
а
в
с
назад
вперед
Или по другому:

Достроим треугольник с катетами а, в и гипотенузой с до квадрата со стороной а+в так, как показано на рисунке.
С одной стороны, площадь этого квадрата
С другой стороны, квадрат составлен из 4-х равных треугольников площадью каждый и квадрата со стороной с, поэтому его площадь:
Уравнивая, получаем:
Откуда
В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ КВАДРАТ ГИПОТЕНУЗЫ РАВЕН СУММЕ КВАДРАТОВ КАТЕТОВ
в
в
в
в
с
с
с
с
а
а
а
а

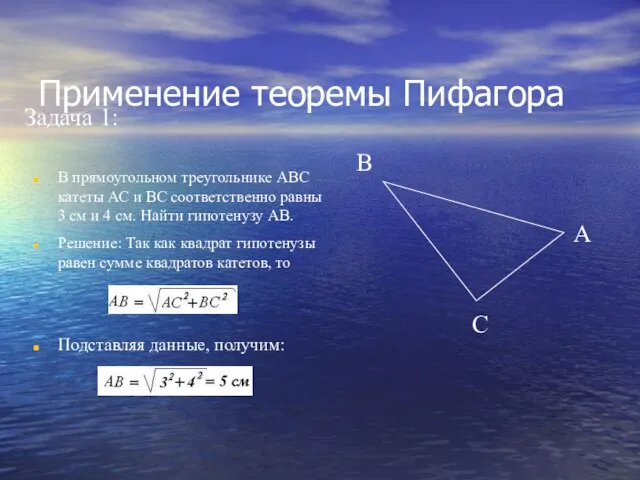
Применение теоремы Пифагора
Задача 1:
В прямоугольном треугольнике АВС катеты АС и ВС соответственно равны 3 см и 4 см. Найти гипотенузу АВ.
Решение: Так как квадрат гипотенузы равен сумме квадратов катетов, то
А
В
С
Подставляя данные, получим:

Применение теоремы Пифагора
Задача 2:
В прямоугольном треугольнике АВС катет АС и гипотенуза АВ соответственно равны 4 см и 6 см. Найти катет ВС.
Решение: Для нахождения длины катета извлечем квадратный корень из разности квадратов гипотенузы и известного катета:
А
В
С
Подставляя данные, получим:

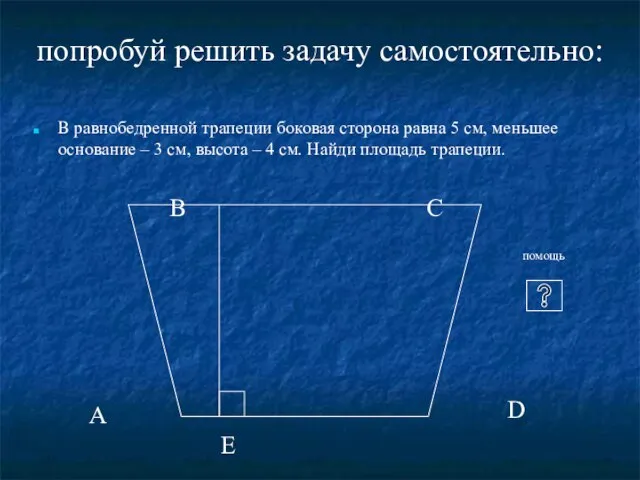
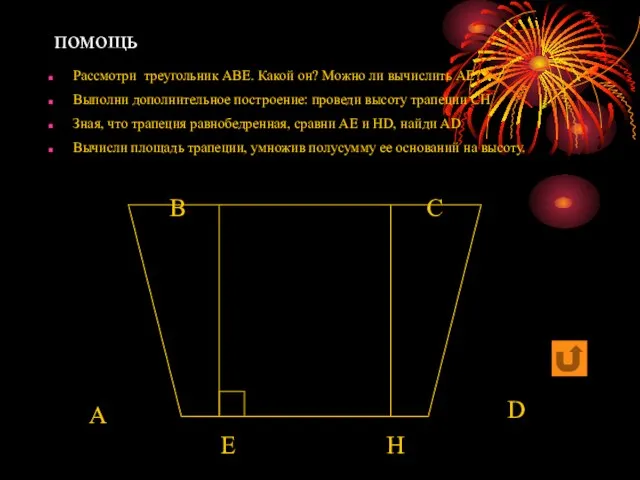
В равнобедренной трапеции боковая сторона равна 5 см, меньшее основание – 3 см, высота – 4 см. Найди площадь трапеции.
А
В
С
D
E
помощь
попробуй решить задачу самостоятельно:

А
В
С
D
E
Рассмотри треугольник АВЕ. Какой он? Можно ли вычислить АЕ?
Выполни дополнительное построение: проведи высоту трапеции СН
Зная, что трапеция равнобедренная, сравни АЕ и НD, найди AD
Вычисли площадь трапеции, умножив полусумму ее оснований на высоту.
Н
помощь