Теоретические и практические вопросы подготовки к ЕГЭ по математике

Статистика
В - 3
В - 10 стереометрия
В – 11 планиметрия
C4 – повышенный уровень сложности

Формулы для площади треугольника

Найдите площадь треугольника ОНС, если на стороне КН треугольника НКО отмечена точка С, так что СН=6, СК=12,
,

Найти площадь треугольника АВС, если АВ= . На стороне СВ взята точка К так, что СК=4, КВ=9,

Найти площадь трапеции если боковые стороны равны 13 и 15, а основания 6 и 10.

Найти площадь трапеции если ее диагонали равны 10 и 17, а основания равны 3 и 18.

Тангенс угла равнобедренной трапеции равен , а радиус вписанной окружности равен 2. Найти среднюю линию трапеции.

Диагонали АС и ВД параллелограмма АВСД пересекаются в точке О, ВД=26, АС=40, ВС=21. Найти разность площадей четырех угольников ДСЕО и АВЕО.

Дан ромб с острым углом В, площадь ромба равна 320, а sinB=0.8, высота СН пересекает диагональ в точке К. Найти длину СК.

Отношение объемов треугольных пирамид имеющих равный трехгранный угол

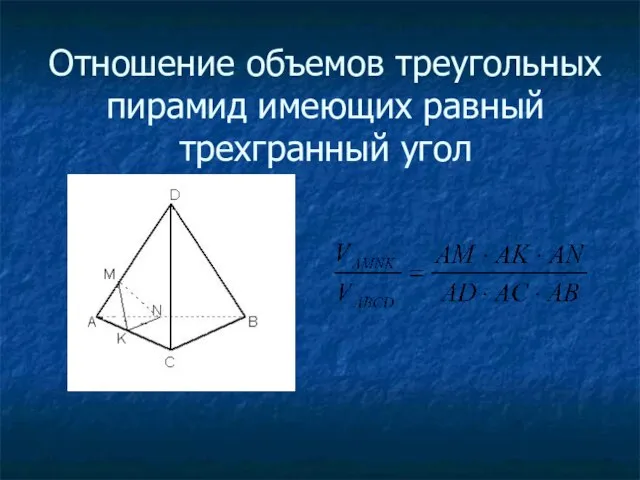
В треугольной пирамиде SABC на ребре SВ взята точка Д так что SД:ДВ=7:3, а на ребре SС точка Е так что SЕ:ЕС=1:4. Сколько процентов составляет объем SDEA от объема SABC.

В треугольной пирамиде ДАВС ребро ДА равно 12 и перпендикулярно основанию АВС, ДВ=ВС=15, ДС=20. На сколько % косинус угла ВСА больше косинуса угла ВДС?

Основание АВС пирамиды А1ВDC вписано в основание цилиндра, АС – диаметр, АВ>ВС, объем пирамиды равен 8. а объем цилиндра равен 48п. Найти градусную меру угла САВ.

АВ –диаметр нижнего основания, а СД –диаметр верхнего основания и СД перпендикулярно АВ. Известно, что площадь треугольника АВС равна 65, а площадь осевого сечения равна 120. Найти высоту цилиндра.

Уровень С4
Многогранники, угол и расстояние между скрещивающимися прямыми;
Тела вращения, угол и расстояние между скрещивающимися прямыми;
Комбинация многогранников;
Комбинация тел вращения;
Комбинация многогранников и тел вращения.