Теоретические основы электротехники. Расчет переходных процессов в разветвленных линейных электрических цепях
Содержание
- 2. Алгоритм расчета переходных процессов в разветвленных линейных электрических цепях классическим методом сначала на основании правил Кирхгофа
- 3. система дифференциальных уравнений алгебраизуется (заменяется системой алгебраических уравнений путем применения оператора дифференцирования; этот пункт можно опустить
- 4. если в составленной схеме нет короткозамкнутых ветвей, то размыкается любая ветвь, определяется входное сопротивление со стороны
- 5. (В случае квадратного характеристического уравнения, т.е. если рассматривается система уравнений второго порядка, возможны три варианта типа
- 7. на основании условий, описывающих состояние системы в послекоммутационный период (в установившемся режиме) находятся принужденные составляющие полных
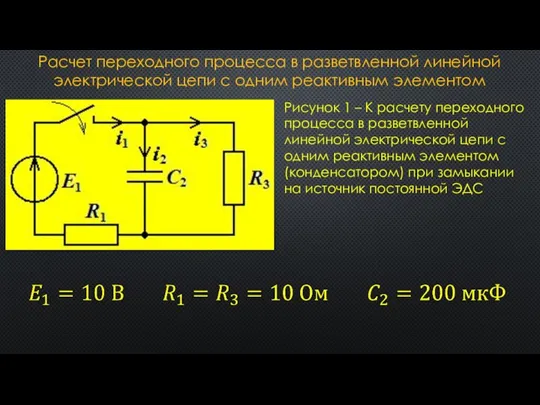
- 8. Расчет переходного процесса в разветвленной линейной электрической цепи с одним реактивным элементом Рисунок 1 – К
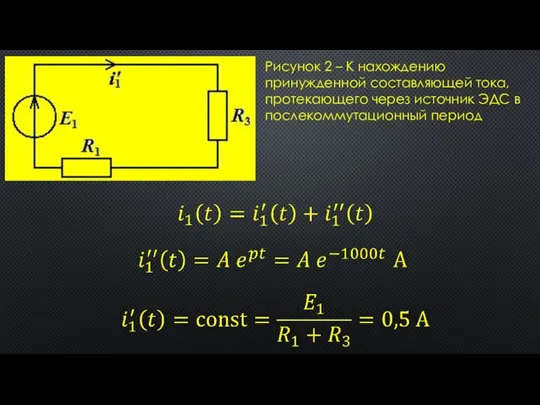
- 10. Рисунок 2 – К нахождению принужденной составляющей тока, протекающего через источник ЭДС в послекоммутационный период
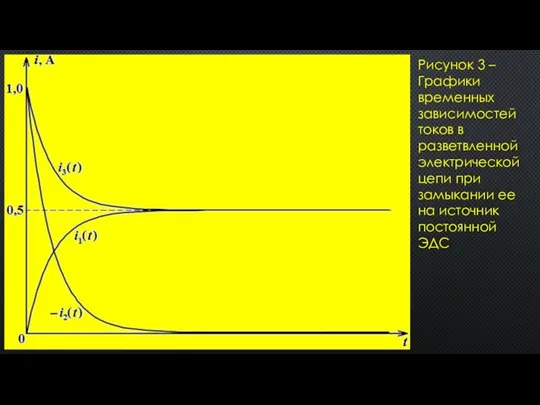
- 13. Рисунок 3 – Графики временных зависимостей токов в разветвленной электрической цепи при замыкании ее на источник
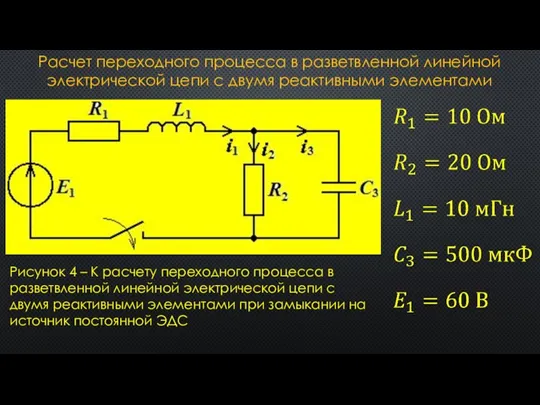
- 14. Расчет переходного процесса в разветвленной линейной электрической цепи с двумя реактивными элементами Рисунок 4 – К
- 25. Скачать презентацию






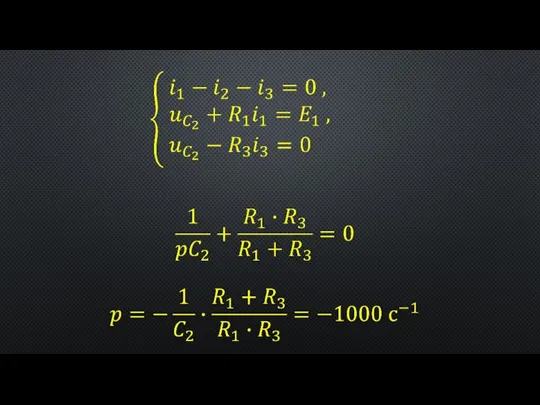
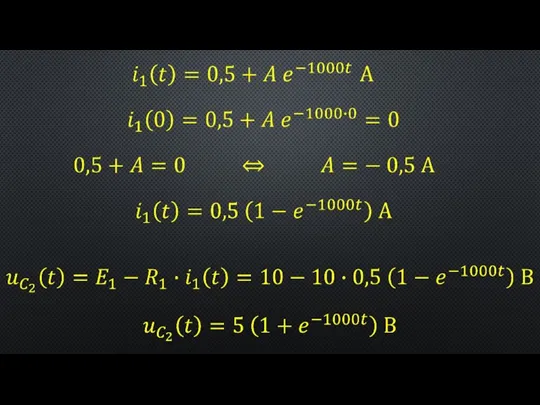
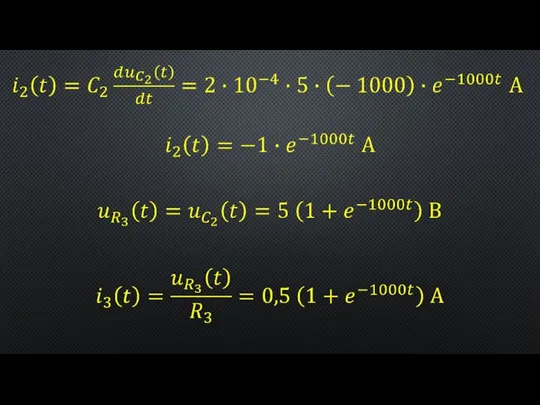
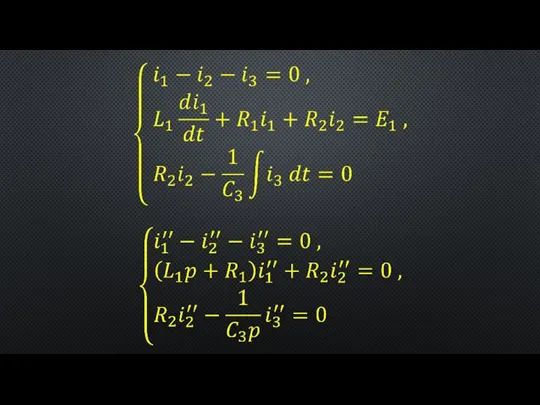

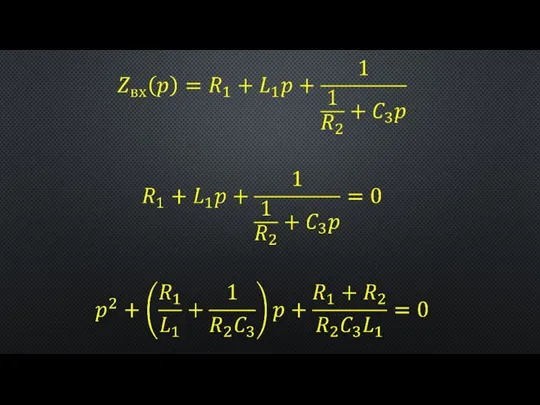
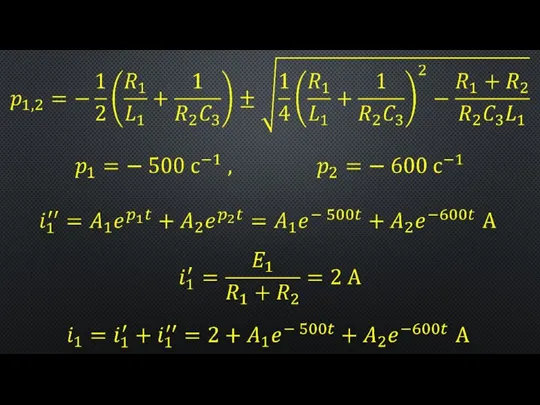
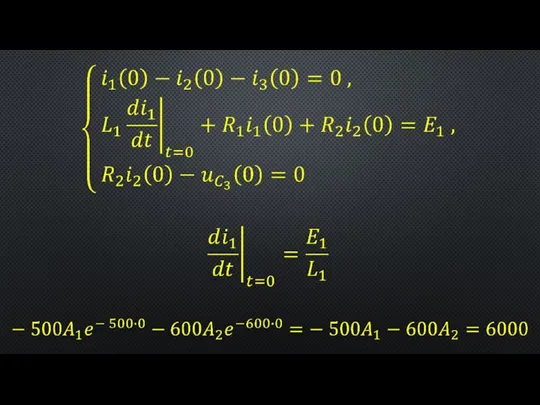
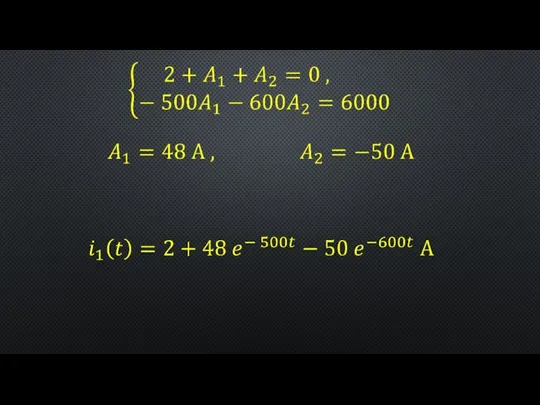
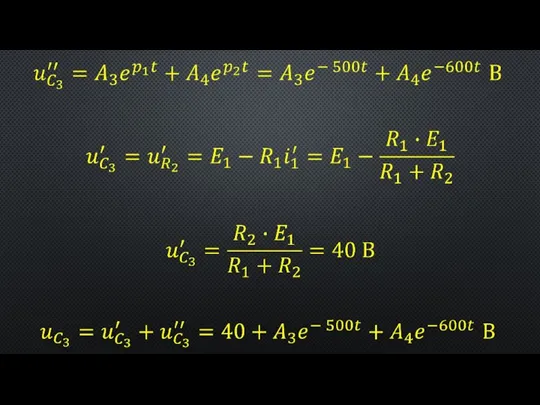
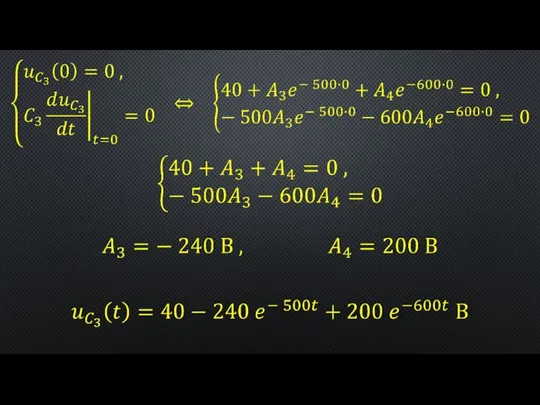
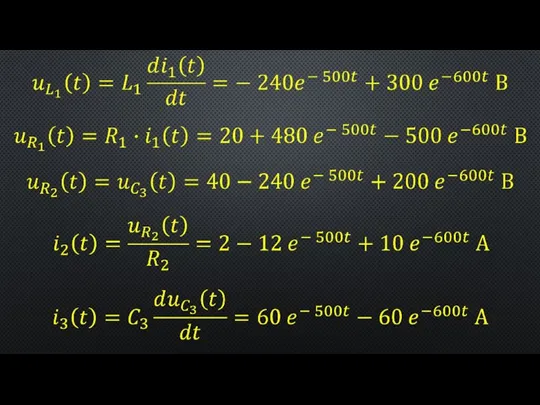
 МОДЕЛИРОВАНИЕ СОВРЕМЕННОЙ МАКРОЭКОНОМИЧЕСКОЙ СИСТЕМЫ: значение отдельных секторов с позиций межстранового анализа Константин П
МОДЕЛИРОВАНИЕ СОВРЕМЕННОЙ МАКРОЭКОНОМИЧЕСКОЙ СИСТЕМЫ: значение отдельных секторов с позиций межстранового анализа Константин П pishchevye-resursy-chelovechestva
pishchevye-resursy-chelovechestva Необычные памятники в англоязычных странах
Необычные памятники в англоязычных странах А.В.Суворов
А.В.Суворов Этапы сделки
Этапы сделки МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕДОШКОЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ДЕТСКИЙ САД № 47 «ЗЕЛЕНЫЙ ОГОНЕК» КОМПЕНСИРУЮЩЕГО ВИДА» г. Север
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕДОШКОЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ДЕТСКИЙ САД № 47 «ЗЕЛЕНЫЙ ОГОНЕК» КОМПЕНСИРУЮЩЕГО ВИДА» г. Север Народные промыслы России
Народные промыслы России Гражданская война 1918-1921 гг.
Гражданская война 1918-1921 гг. Современные технологии мерчендайзинга и программные инструменты для их реализации
Современные технологии мерчендайзинга и программные инструменты для их реализации Налоги
Налоги Юскинской школе 130 лет
Юскинской школе 130 лет Презентация на тему Источники электрического тока
Презентация на тему Источники электрического тока  Образы-символы в трилогии Дж. Р. Р. Толкиена «Властелин колец»
Образы-символы в трилогии Дж. Р. Р. Толкиена «Властелин колец» Весенняя студенческая энергетическая школа. Кейс по РЗА
Весенняя студенческая энергетическая школа. Кейс по РЗА Презентация на тему Спасская башня
Презентация на тему Спасская башня Оценка репутационного риска банка
Оценка репутационного риска банка Пространство и размерность
Пространство и размерность Анализ достаточности финансовых ресурсов МО г. Новодвинск
Анализ достаточности финансовых ресурсов МО г. Новодвинск Этапы преобразований в экономике в 1990-е г.г. Этапы преобразований в экономике в 1990-е г.г. «Шоковая терапия» в экономике. Корректиро
Этапы преобразований в экономике в 1990-е г.г. Этапы преобразований в экономике в 1990-е г.г. «Шоковая терапия» в экономике. Корректиро Правовой стиль и правовые семьи по К. Цвайгерту и Х. Кётцу
Правовой стиль и правовые семьи по К. Цвайгерту и Х. Кётцу Спроектировать участок сборо-сварочного цеха по изготовлению Опоры Оп1-1 для серийного типа
Спроектировать участок сборо-сварочного цеха по изготовлению Опоры Оп1-1 для серийного типа Социальная интеграция инвалидов в Приволжском федеральном округе
Социальная интеграция инвалидов в Приволжском федеральном округе Использование упражнений по развитию мышления на уроках географии в 6 классе.
Использование упражнений по развитию мышления на уроках географии в 6 классе. Спортплощадка Обская
Спортплощадка Обская Английская буржуазная революции
Английская буржуазная революции Конституция РФ (9 класс)
Конституция РФ (9 класс) Маркетинг в здравоохранении
Маркетинг в здравоохранении Звуковые сигналы на железнодорожном транспорте. Сигналы тревоги и специальные указатели
Звуковые сигналы на железнодорожном транспорте. Сигналы тревоги и специальные указатели