Содержание
- 2. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ Работа, совершаемая статически приложенной силой Fi , равна сумме элементарных Итак, Получено простое
- 3. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ Внутренние усилия препятствуют развитию деформации тела, поэтому при нагружении тела, не имеющего начальных
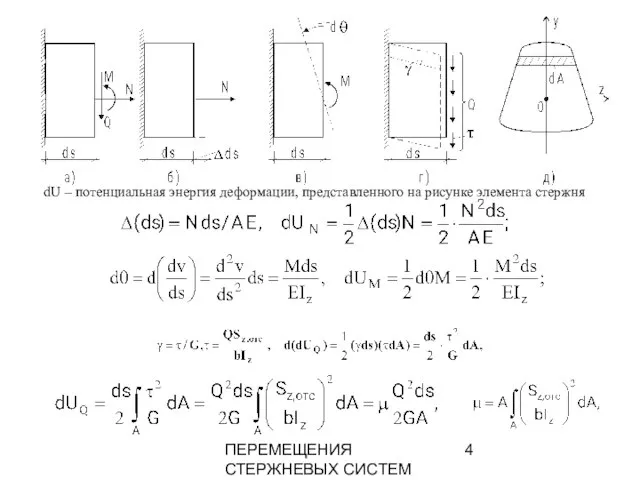
- 4. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ dU – потенциальная энергия деформации, представленного на рисунке элемента стержня
- 5. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ Потенциальная энергия упругой деформации плоской стержневой системы Виртуальными или возможными называют малые перемещения
- 6. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ 2. Метод Максвелла–Мора определения перемещений плоских стержневых систем Вывод разрешающих соотношений метода базируется
- 7. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ Работа внутренних сил фиктивного состояния на возможных перемещениях Возможная работа силы равна Для
- 8. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ 3. Техника определения перемещений Выбор фиктивного состояния определяется видом искомого перемещения: При определении
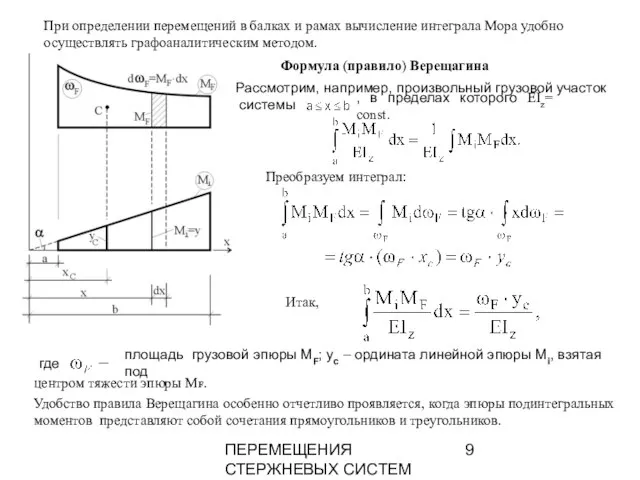
- 9. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ При определении перемещений в балках и рамах вычисление интеграла Мора удобно осуществлять графоаналитическим
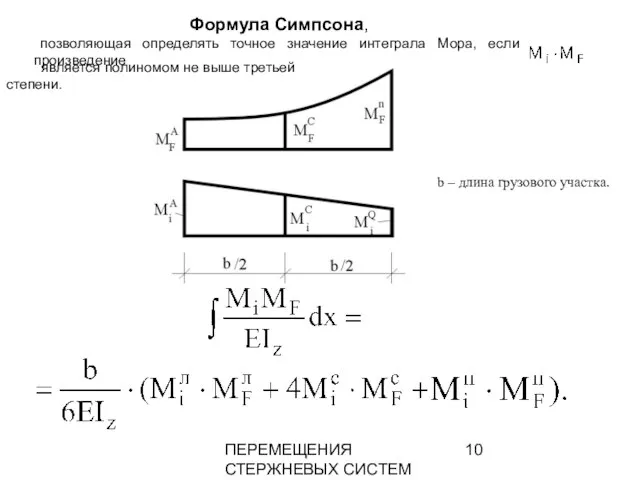
- 10. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ Формула Симпсона, позволяющая определять точное значение интеграла Мора, если произведение является полиномом не
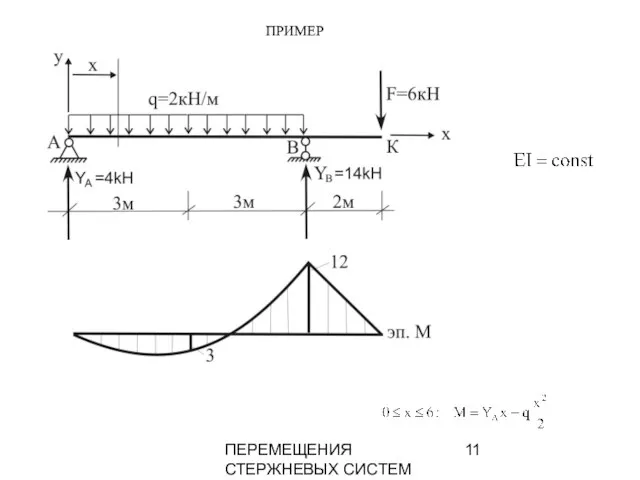
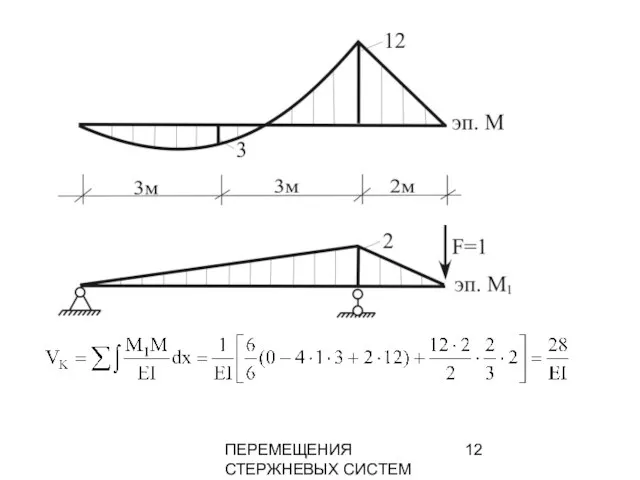
- 11. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ ПРИМЕР
- 12. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ
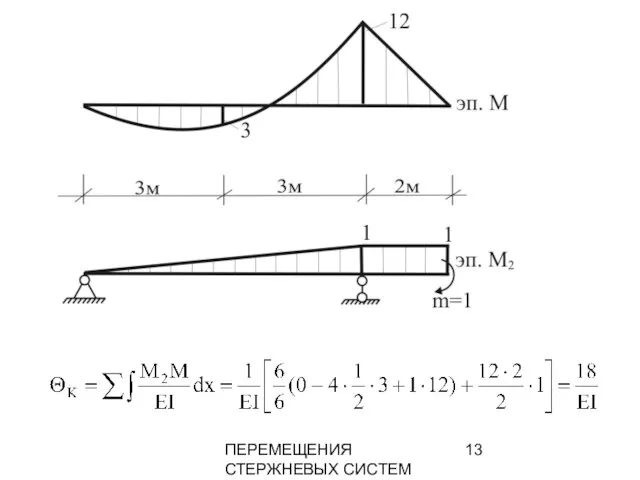
- 13. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ
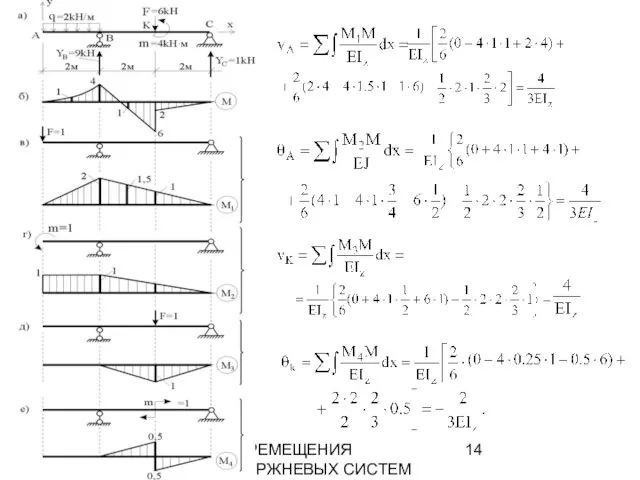
- 14. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ
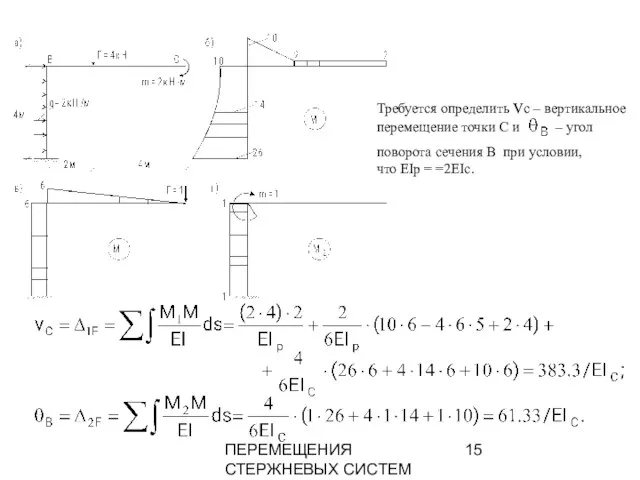
- 15. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ поворота сечения В при условии, что EIp = =2EIc. Требуется определить vc –
- 16. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ Теоремы взаимности В приложении к линейно-деформируемым стержневым системам можно утверждать, что в процессе
- 17. ПЕРЕМЕЩЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ Рассмотрим два варианта последовательных загружений системы силами Fi, Fk и определим совершаемые при
- 19. Скачать презентацию








 Основы автоматики и системы автоматического управления
Основы автоматики и системы автоматического управления Основные риски реализации проекта информатизации здравоохранения в 2012 году и возможные пути их преодоления
Основные риски реализации проекта информатизации здравоохранения в 2012 году и возможные пути их преодоления Культурные достижения Востока
Культурные достижения Востока Структура объединенного ньюс-рума, принципы планирования и движения мультимедийного контента
Структура объединенного ньюс-рума, принципы планирования и движения мультимедийного контента Досвед удзелу грамадскіх аб’яднанняў Гродна ў развіцці супрацоўніцтва ў межах Еўрарэгіёну “Нёман”(2001-2010)
Досвед удзелу грамадскіх аб’яднанняў Гродна ў развіцці супрацоўніцтва ў межах Еўрарэгіёну “Нёман”(2001-2010) История суверенного Казахстана, роль Первого Президента Республики Казахстан в становлении и развитии страны
История суверенного Казахстана, роль Первого Президента Республики Казахстан в становлении и развитии страны Требования к выпускным работам слушателей
Требования к выпускным работам слушателей Управления освещением
Управления освещением Искусство средневекового фарса
Искусство средневекового фарса 20141020_kachestvo_zhizni_prezentatsiya_na_sots_set_rab_obr
20141020_kachestvo_zhizni_prezentatsiya_na_sots_set_rab_obr Стиль в живописи: пуантилизм
Стиль в живописи: пуантилизм О КОМПАНИИ ООО «Аграрная инвестиционная компания «Агрико» - одна из самых динамично развивающихся крупных холдинговых структур а
О КОМПАНИИ ООО «Аграрная инвестиционная компания «Агрико» - одна из самых динамично развивающихся крупных холдинговых структур а 1С:Предприятие 8 «1С:Пиво-безалкогольный комбинат»
1С:Предприятие 8 «1С:Пиво-безалкогольный комбинат» Создание условий для работы с детьми с ограниченными возможностями здоровья
Создание условий для работы с детьми с ограниченными возможностями здоровья tipy_vneshnosti
tipy_vneshnosti Создание высокодоходного предприятия
Создание высокодоходного предприятия Презентация на тему Теорема Пифагора
Презентация на тему Теорема Пифагора (Методические рекомендации)
(Методические рекомендации) Презентация на тему: Дифференциация звуков [р]-[л] в словах и предложениях
Презентация на тему: Дифференциация звуков [р]-[л] в словах и предложениях Дебаттың ойын ережесі
Дебаттың ойын ережесі Унөченче
Унөченче СПА-уход для Вас. История Гальванического тока В 1791году, Луиджи Гальвани, итальянский учёный, изучал гальванические токи в целях оп
СПА-уход для Вас. История Гальванического тока В 1791году, Луиджи Гальвани, итальянский учёный, изучал гальванические токи в целях оп Альфред Бернхард Нобель
Альфред Бернхард Нобель трудовой кодекс
трудовой кодекс Лечебно-консультативная работа Сотрудниками кафедры ежегодно выполняется около 1200 наиболее сложных оперативных вмешательств (ок
Лечебно-консультативная работа Сотрудниками кафедры ежегодно выполняется около 1200 наиболее сложных оперативных вмешательств (ок РИМСКОЕ ПРАВО
РИМСКОЕ ПРАВО Секреты подготовки к экзаменам. Беседа с элементами тренинга для обучающихся
Секреты подготовки к экзаменам. Беседа с элементами тренинга для обучающихся Hydraulik I
Hydraulik I