Теория радиоактивных методов

Радиоактивность осадочных горных пород. Радионуклиды.
Гамма-излучение калия (40К) монохроматично - 1,46 МэВ. Энергетические спектры элементов урановых (238U, 235U) и ториевого (232Th) рядов имеют несколько линий, наиболее интенсивные— 242, 355, 609, 1120, 1765 кэВ и 238, 338, 583, 911, 969, 1587, 2620 кэВ соответственно.

*
Активность а одного кубического метра вещества называют удельной объемной активностью.
Величину am=a/δ (δ — плотность вещества) называют удельной массовой активностью.
Для практических целей используют удельную объемную концентрацию Qj, определяющую содержание j-го естественного радиоактивного элемента (ЕРЭ) в граммах в 1 сантиметре кубическом,
и относительную величину — удельную массовую концентрацию
qj = Qj / δ.
Радиоактивность горных пород

*
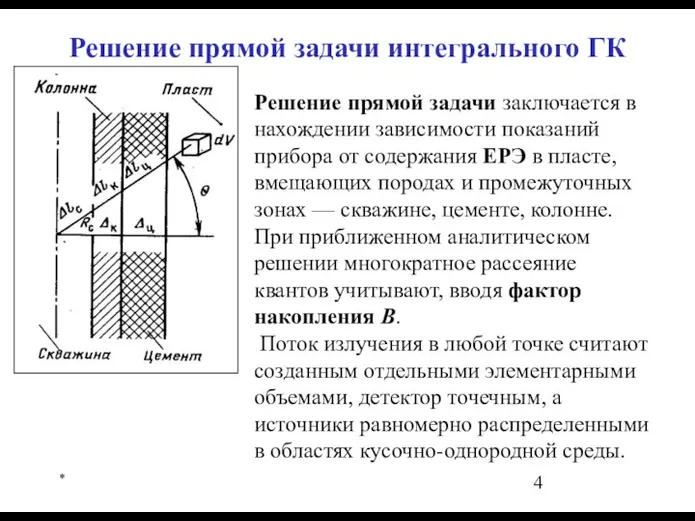
Решение прямой задачи интегрального ГК
Решение прямой задачи заключается в нахождении зависимости показаний прибора от содержания ЕРЭ в пласте, вмещающих породах и промежуточных зонах — скважине, цементе, колонне.
При приближенном аналитическом решении многократное рассеяние квантов учитывают, вводя фактор накопления В.
Поток излучения в любой точке считают созданным отдельными элементарными объемами, детектор точечным, а источники равномерно распределенными в областях кусочно-однородной среды.

*
Решение прямой задачи интегрального ГК
Плотность потока излучения кусочно-однородного
пространства
где аj — удельная объемная активность j-го ЕРЭ;
Bj – фактор накопления j-го ЕРЭ;
μij — коэффициент ослабления излучения j-го ЕРЭ в i-й среде, расположенной между точками r и r1;
Δli — длина части отрезка, соединяющего точки r и r1 в среде i.

*
Решение прямой задачи интегрального ГК
Плотность потока излучения для однородной среды с точечным детектором в начале координат

Решение прямой задачи интегрального ГК
Так как
Получаем
где: λpj – параметр распада (вероятность распада за единицу времени) j-го ЕРЭ; Nj /dV - число ядер j-го ЕРЭ в единице объема; NA - число Авогадро; Aj - атомная масса j-го ЕРЭ;
Qj - объемная концентрация j-го ЕРЭ ; μmj = μj /δ - массовый коэффициент ослабления излучения j-го ЕРЭ.
qj = Qj / δ

Решение прямой задачи интегрального ГК
Показания скважинного прибора в однородной среде, содержащей j-й ЕРЭ,
где сj – аппаратурная постоянная.
Введя коэффициент концентрационной чувствительности (Сj), характеризующий отклик прибора на излучение единицы удельной массовой концентрации j-го ЕРЭ,
получим выражение в более компактной форме:
Ij = Cj qj.

Решение прямой задачи интегрального ГК. Урановый эквивалент.
Показания скважинного прибора в однородной
среде, содержащей j-й ЕРЭ,
Ij = CU qj eUj .
где CU – коэффициент концентрационной чувствительности по урану.
qj – удельные массовые концентрации урана (U), тория (Th) и калия (K).
eUj – урановые эквиваленты единичной концентрации урана (U), тория (Th) и калия (K).
Суммарное показание гамма-каротажа
Iγ= CU ∑qj eUj

Суммарная удельная массовая концентрация радионуклидов
Суммарная удельная массовая концентрация смеси радионуклидов в единицах уранового эквивалента
∑qj eUj = Iγ / CU,
где - Iγ = ∑ Ij скорость счета, зарегистрированная с помощью интегральной аппаратуры гамма-каротажа.
Коэффициент СU, позволяющий перейти от импульсов в единицу времени к суммарной концентрации радионуклидов в 1 грамме породы, определяют экспериментально с помощью образцового источника γ-излучения.

*
Решение прямой задачи интегрального ГК
Для кусочно-однородной среды, содержащей пласт бесконечной мощности, плотность потока излучения равна сумме плотностей потоков, обусловленных пластом, скважиной, колонной и цементом
Ф = Фпл + Фс + Фк + Фц.
В сферической системе координат
Δlc = Rc / cosθ; Δlк = Δк / cosθ;
Δlц = Δц / cosθ;
Δlпл = r - ( Rc+Δк+Δц ) / cosθ

*
Решение прямой задачи интегрального ГК
Поток излучения пласта Фплj, содержащего j-и ЕРЭ
Где
Δ = Δцμцj + Δкμкj + Rcμcj
Ф = Фпл + Фс + Фк + Фц

*
Решение прямой задачи ГК. Геометрический фактор.
Плотность Фплj пропорциональна коэффициенту G(Δ), который зависит от геометрии системы, коэффициентов μцj , μкj , μcj и характеризует вклад данной области в регистрируемый сигнал.
По существу G(Δ) – аналог геометрического фактора. Для кусочно-однородной среды, содержащей К областей с j-м ЕРЭ

*
Решение прямой задачи ГК. Геометрический фактор.
Введя геометрические факторы колонны Gjk , цемента Gjц , скважины Gjс , пласта Gjпл=G(Δ), и переходя к показаниям прибора, для среды, содержащей смесь ЕРЭ, запишем:
Геометрические факторы областей мало зависят от типа ЕРЭ. Поэтому уравнение при однородной промежуточной зоне
- суммарная массовая удельная концентрация ЕРЭ в скважине, цементе и колонне.
Iγ= CU ∑qj eUj

*
Решение прямой задачи ГК. Пласт конечной мощности
Пласт конечной мощности, пересеченный необсаженной скважиной, вызывает приращение плотности потока
ΔФ = Фпл - Фвм,
где Фвм — плотность потока излучения во вмещающих породах. Если параметры В, μж и G против пласта и вмещающих пород практически равны, то ΔФ равно плотности потока при массовой активности Δа = апл - авм, где авм — удельная объемная активность вмещающих пород.
Подставив в вышеприведенные формулы Δа, получим выражение для ΔФпл, позволяющее рассчитать диаграммы ГК против пласта с заданными параметрами, для случая для υτя=0.

Решение прямой задачи ГК. Диаграммы ГК против пластов конечной мощности.
Детекторы: 1 – точечный, 2 – длиной 2Rc=30 см; μпл=0,1см-1; δпл=3г/см3

*
Первичный спектр естественного гамма-излучения пород дает представления о распределении его интенсивности по энергиям. Этот спектр содержит характерные максимумы, соответствующие энергиям определенных ЕРЭ.
Аппаратурный спектр гамма-излучения породы отмечает максимумы первичного спектра, соответствующие энергиям 0,6 и 1,8 МэВ для радия (урана); 0,9; 1,6 и 2,6 МэВ для тория; 1,46 МэВ для калия.
Дифференциальный спектр характеризует интенсивность Iγ естественного гамма-излучения в заданном диапазоне энергии ΔЕ, причем каждый диапазон исследуется отдельным каналом.
Спектрометрический гамма-каротаж. СГК

*
Для определения удельных массовых концентраций qu, qTh, qK по интенсивностям Iγ1, Iγ2, Iγ3, зарегистрированным первым, вторым и третьим каналами, решают систему уравнений:
Коэффициенты в уравнениях, для конкретного радиометра, определяют путем эталонирования прибора.
Спектрометрический гамма-каротаж. СГК