Тестирование автокорреляции

Понятие автокорреляции
Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui,uj)≠0 при i≠j.
Автокорреляция чаще всего появляется в моделях временных рядов и моделировании циклических процессов.
Причина – неправильный выбор спецификации модели.
Последствия автокорреляции.
- оценки коэффициентов теряют эффективность;
- стандартные ошибки коэффициентов занижены.

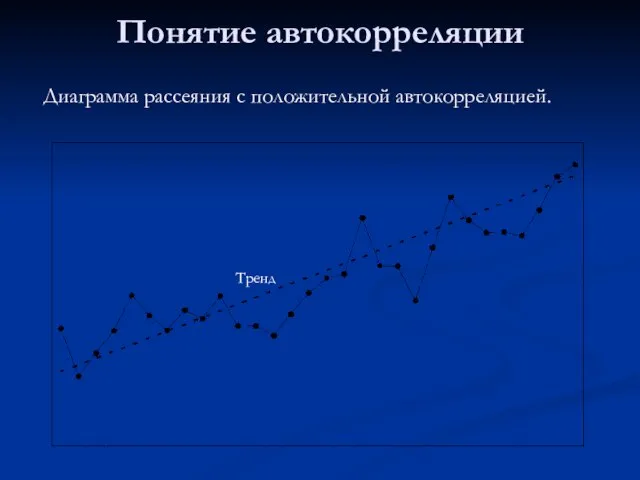
Понятие автокорреляции
Тренд
Диаграмма рассеяния с положительной автокорреляцией.

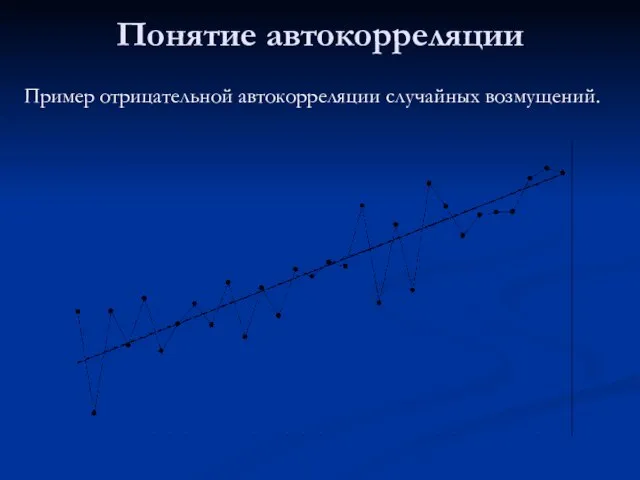
Понятие автокорреляции
Пример отрицательной автокорреляции случайных возмущений.

Типы автокорреляции
Авторегрессия 1-го порядка : AR(1)
Авторегрессия 5-го порядка : AR(5)
Авторкорреляция скользящих средних 3-го порядка:
Рассматриваем модель парной регрессии.

Тест Дарбина-Уотсона
1. Предпосылки теста.
Случайные возмущения распределены по нормальному закону.
Имеет место авторегрессия первого порядка:
2. Статистика для проверки гипотезы:
М(εt)=0; σ2(εt)=Const

Тест Дарбина-Уотсона
3. Свойства статистики DW.
где: r- коэффициент корреляции между случайными возмущениями.
Из этого выражения следует:
DW изменятся в пределах (0 – 4).
При этом если r = 1, DW=0- положительная корреляция;
если r = 0, DW=2-; отсутствие корреляции;
если r=-1, DW=4- отрицательная корреляция.

Тест Дарбина-Уотсона
Для статистики DW не возможно найти критическое значение, т.к. оно зависит не только от Рдов и степеней свободы k и n-1, но и от абсолютных значений регрессоров.
Возможно определить границы интервала DL и Du внутри которого критическое значение DWкр находится:
DL ≤ DWкр ≤ Du
Значения Du и DL находятся по таблицам.

Тест Дарбина-Уотсона
Нет автокорреляции
Положительная автокорреляция
Отрицательная автокорреляция
Интервалы (DL, Du) и (4-DL, 4-Du) зоны неопределенности.
10
2
4
0
dL
dU
dcrit
положительная автокорреляция
отрицательная автокорреляция
нет автокорреляции
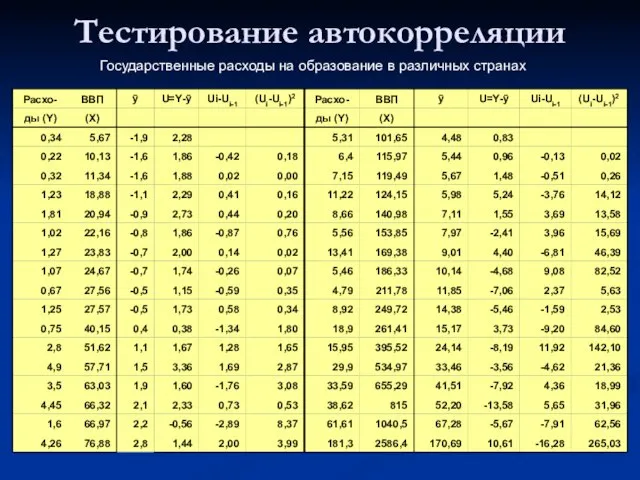
dcrit

Тестирование автокорреляции
Государственные расходы на образование в различных странах

Тестирование автокорреляции
Модель: Y=-2.32 + 0.669X +U
(0.9) (0.002)
ESS=ΣUi2=710.34
Σ(Ui-Ui-1)2 = 832.4
DW = 832.4/710.3=1.17
Границы интервала – dL=1.35; du=1.49
DW< dL
Вывод: модель автокоррелирована

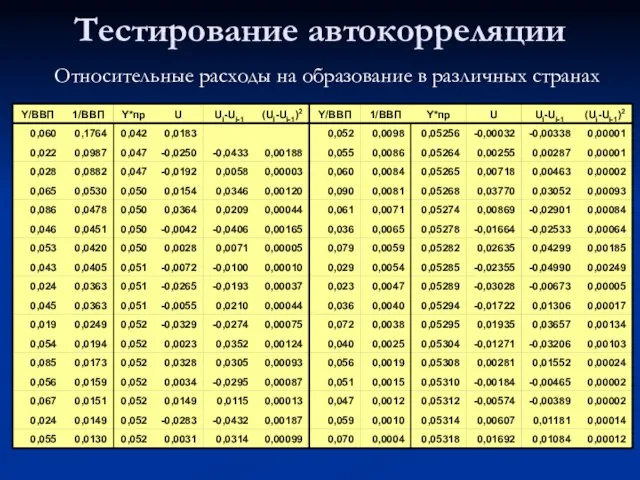
Тестирование автокорреляции
Относительные расходы на образование в различных странах

Тестирование автокорреляции
Модель: 0.0530 - 0.66Х +U
(0.004) (0.1)
ESS=ΣUi2=0.012
Σ(Ui-Ui-1)2 = 0.0229
DW = 0.0229/0.012=1.79
Границы интервала – dL=1.35; du=1.49
dL
Вывод: модель неавтокоррелирована

Метод исправления автокорреляции
Рассматривается случай авторегрессии первого порядка:
Yt=a0+a1x1t+a2x2t+Ut
Ut =ρUt-1+εt
При этом:
M(εt)=0 σ2(εt ) = σ2t |ρ|<1
Тогда:
σ2(Ut ) = ρ2 σ2(Ut-1 ) + σ2t + 2Cov(ρ,Ut-1)
Cov(ρ,Ut-1)=0 , т.к. ρ=Const
Следовательно
σ2(Ut ) = ρ2 σ2(Ut-1 ) + σ2t (10.1)

Метод исправления автокорреляции
Множитель (1-ρ2) обеспечивает стационарность σ2(Ut), т.е. постоянство σ2(Ut)
(10.2)
Т.к. U0 отсутствует, полагаем, что σ2(U1) =σ2(U0)
Тогда из (10.1) следует:
Выражение (10.2) – начальное условие для σ2(U0)
Из выражения (10.1) с учетом (10.2) вытекает:

Метод исправления автокорреляции
Для произвольного наблюдения t в силу рекурентности (10.1) имеем:
(10.3)
Вывод: введение корректирующего множителя (1-ρ2) обеспечивает постоянство σ2(U) во всех наблюдениях и, следовательно, отсутствие автокорреляции между случайными возмущениями.

Метод устранения автокорреляции
Рассмотрим два последовательных уравнения наблюдения
(10.4)
(10.5)
Умножим уравнение (10.5) на ρ и вычтем из (10.4)
Учитывая, что Ut-ρUt-1=εt и делая замену переменных
получим систему уравнений, в которых дисперсия случайных возмущений постоянна.
(10.6)